Расстояние между гиперплоскостями

Я пытаюсь научить себя некоторому машинному обучению и использую базу данных MNIST (http://yann.lecun.com/exdb/mnist/) Сделайте так. Автор этого сайта написал статью в 98 году о различных методах распознавания почерка, доступных по адресу http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf.

упомянутый 10-й метод является "классификатором касательных расстояний". Идея в том, что если вы поместите каждое изображение в (НХМ)-мерных векторное пространство, вы можете вычислить расстояние между двумя изображениями как расстояние между гиперплоскости, образованной каждого, где гиперплоскость задается принимаете точку, и поворот изображения, масштабирование изображения, преобразование изображения и т. д.

Я не могу понять достаточно, чтобы восполнить недостающие детали. Я понимаю, что большинство из них действительно являются линейными операторами, так как же использовать этот факт для создания гиперплоскости? И если у нас есть гиперплоскость, как мы можем взять ее расстояние? с другими гиперплоскостями?

8
classification image-processing image-recognition machine-learning math

1 ответов

я дам вам несколько подсказок. Вам нужны базовые знания в обработке изображений. Пожалуйста, обратитесь к 2,3 для сведения.

  • 2 это c реализация тангенциальной составляющей
  • 3 это документ, который описывает касательное расстояние более подробно

Свертка Изображения

по данным 3, первый шаг вам нужно сделать, это сгладьте картинку. Ниже мы покажем результат 3 различных плавных операций (проверьте раздел 4 из 3) (левый столбец показывает изображения результата, правый столбец показывает исходные изображения и операторы свертки). Этот шаг заключается в отображении дискретного вектора на непрерывный, чтобы он был дифференцируемым. Автор предлагает использовать функцию Гаусса. Если вам нужно больше фона о свертке изображения,здесь пример.

enter image description here

после выполнения этого шага вы рассчитали горизонтальный и вертикальный сдвиг:

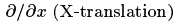
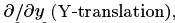
enter image description hereenter image description here

Вычисление Тангенса Масштабирования

здесь я покажу вам один из касательных вычислений, реализованных в 2 - масштабирование касательной. От 3, мы знаем, что преобразование, как показано ниже:

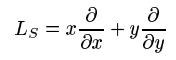
enter image description here

/* scaling */
for(k=0;k<height;k++)
  for(j=0;j<width;j++) {
    currentTangent[ind] = ((j+offsetW)*x1[ind] + (k+offsetH)*x2[ind])*factor;
    ind++;
  }

в начале td.c in 2реализация, мы знаем следующее определение:

factorW=((double)width*0.5);
offsetW=0.5-factorW;
factorW=1.0/factorW;

factorH=((double)height*0.5);
offsetH=0.5-factorH;
factorH=1.0/factorH;

factor=(factorH<factorW)?factorH:factorW; //min

автор использует изображения размером 16x16. Так мы знаем!--28--> 

factor=factorW=factorH=1/8,

и 

offsetH=offsetW = 0.5-8 = -7.5

также обратите внимание, что мы уже вычислили

  • x1[ind] = ,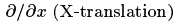
  • x2[ind] =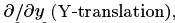

Итак, мы подключаем эти константы:

currentTangent[ind] = ((j-7.5)*x1[ind] + (k-7.5)*x2[ind])/8
                    = x1 * (j-7.5)/8 + x2 * (k-7.5)/8.

С j(кроме k) - целое число от 0 до 15 включительно (ширина и высота изображения 16 пикселей), (j-7.5)/8 это всего лишь дробное число между -0.9375 to 0.9375.

так что я думаю (j+offsetW)*factor - смещение для каждого пикселя, пропорциональное горизонтальному расстоянию от пикселя до центра изображения. Точно так же вы знаете вертикальное смещение (k+offsetH)*factor.

Расчет Тангенса Вращения

тангенс вращения определен как ниже в 3:

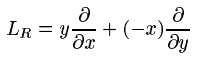
enter image description here

/* rotation */
for(k=0;k<height;k++)
  for(j=0;j<width;j++) {
    currentTangent[ind] = ((k+offsetH)*x1[ind] - (j+offsetW)*x2[ind])*factor;
    ind++;
  }

С помощью вывод из предыдущего, мы знаем!--17--> соответствует y. Аналогично - (j+offsetW)*factor соответствует -x. Таким образом, вы знаете, что это именно формула, используемая в 3.

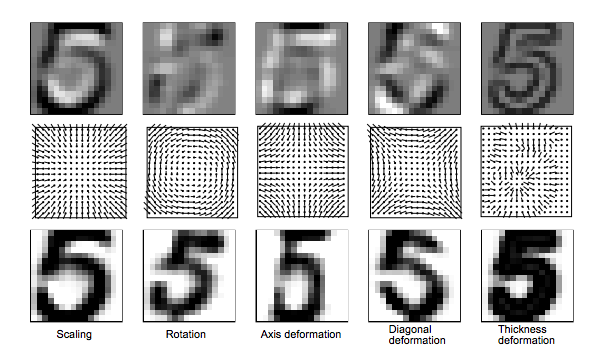
вы можете найти все другие касательные, описанные в 3 реализовала в 2. Мне нравится изображение ниже от 3, который ясно показывает влияние смещений различные касательные преобразования. enter image description here

расчет касательного расстояния между изображениями

просто следуйте реализации в tangentDistance функция:

// determine the tangents of the first image
calculateTangents(imageOne, tangents, numTangents, height, width, choice, background);

// find the orthonormal tangent subspace 
numTangentsRemaining = normalizeTangents(tangents, numTangents, height, width);

// determine the distance to the closest point in the subspace
dist=calculateDistance(imageOne, imageTwo, (const double **) tangents, numTangentsRemaining, height, width);

я думаю, что выше должно быть достаточно, чтобы вы начали, и если что-либо отсутствует, пожалуйста, прочитайте 3 внимательно и смотрите соответствующие реализации в 2. Удачи!

12