Равномерно распределить X точек внутри окружности

Я хотел бы равномерно распределить заданный набор точек внутри круга. Под равномерным распределением я имею в виду, что все они должны быть одинаково удалены друг от друга (следовательно, случайный подход не будет работать). Я попробовал гексагональный подход, но у меня были проблемы с последовательным достижением внешнего радиуса.

мой текущий подход-это вложенный цикл for, где каждая внешняя итерация уменьшает радиус и количество точек, а каждый внутренний цикл равномерно отбрасывает точки на новый радиус. По сути, это куча вложенных кругов. К сожалению, это далеко не так. Любые советы о том, как сделать это правильно?

Nested for-loop result

10
geometry math

1 ответов

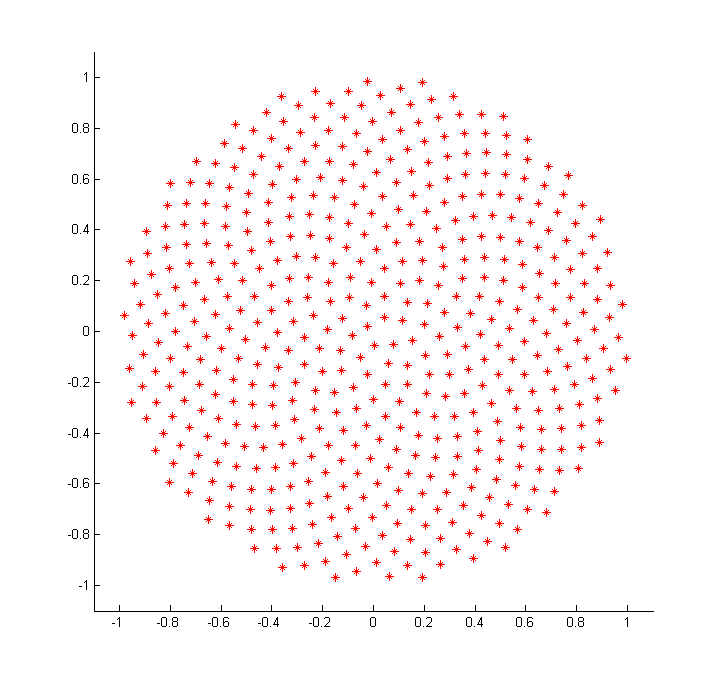
цели иметь равномерное распределение внутри зона и равномерное распределение на конфликте границы; любое разрешение будет компромиссом между 2. Я увеличил семя подсолнуха композиция с дополнительным параметром alpha это указывает на то, насколько человек заботится о равномерности границы.

alpha=0 дает типичное расположение подсолнечника, с зубчатой границей:

alpha0

С alpha=2 в граница более гладкая:

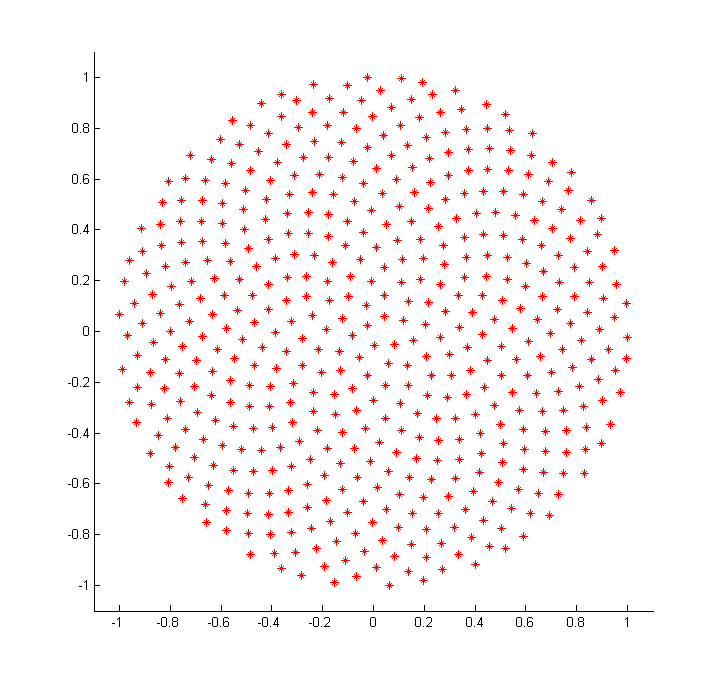
alpha2

(дальнейшее увеличение Альфа проблематично: слишком много точек заканчиваются на границе).

алгоритм местах n точки, из которых k - й пункт ставится на расстоянии sqrt(k-1/2) от границы (индекс начинается с k=1), и с полярным углом 2*pi*k/phi^2 здесь phi золотое сечение. Исключение: последнее alpha*sqrt(n) точки размещают на внешней границе круга, а полярный радиус другой очки масштабируются, чтобы учесть это. Это вычисление полярного радиуса выполняется в функции radius.

он закодирован в MATLAB.

function sunflower(n, alpha)   %  example: n=500, alpha=2
    clf
    hold on
    b = round(alpha*sqrt(n));      % number of boundary points
    phi = (sqrt(5)+1)/2;           % golden ratio
    for k=1:n
        r = radius(k,n,b);
        theta = 2*pi*k/phi^2;
        plot(r*cos(theta), r*sin(theta), 'r*');
    end
end

function r = radius(k,n,b)
    if k>n-b
        r = 1;            % put on the boundary
    else
        r = sqrt(k-1/2)/sqrt(n-(b+1)/2);     % apply square root
    end
end
16