для этого отлично подходит алгоритм сферы Фибоначчи. Это быстро и дает результаты, которые с первого взгляда легко обмануть человеческий глаз. вы можете увидеть пример, выполненный с обработкой который покажет результат с течением времени, как добавляются очки. вот еще один отличный интерактивный пример сделано @gman. И вот быстрая версия python с простым вариантом рандомизации:

import math, random

def fibonacci_sphere(samples=1,randomize=True):
    rnd = 1.
    if randomize:
        rnd = random.random() * samples

    points = []
    offset = 2./samples
    increment = math.pi * (3. - math.sqrt(5.));

    for i in range(samples):
        y = ((i * offset) - 1) + (offset / 2);
        r = math.sqrt(1 - pow(y,2))

        phi = ((i + rnd) % samples) * increment

        x = math.cos(phi) * r
        z = math.sin(phi) * r

        points.append([x,y,z])

    return points

1000 образцов дает вам это:

Это известно как точки упаковки на сфере, и нет (известного) общего, идеального решения. Однако существует множество несовершенных решений. Тремя самыми популярными кажутся:

1. создать имитацию. Рассматривайте каждую точку как электрон, ограниченный сферой, затем выполните моделирование для определенного количества шагов. Отталкивание электронов естественным образом приведет систему к более стабильному состоянию, где точки находятся примерно на таком же расстоянии от каждого другие, насколько это возможно.
2. отказ Гиперкуб. Этот причудливый метод на самом деле очень прост: вы равномерно выбираете точки (гораздо больше, чем n из них) внутри куба, окружающего сферу, затем отклоните точки вне сферы. Рассматривайте оставшиеся точки как векторы и нормализуйте их. Это ваши "образцы" - выберите n из них, используя какой-то метод (случайно, жадный и т. д.).
3. спираль приближения. Вы проводите спираль вокруг сферы и равномерно распределяете точки вокруг спирали. Из-за математики они сложнее понять, чем моделирование, но намного быстрее (и, вероятно, с меньшим количеством кода). Самым популярным кажетсяSaff, et al.

A много более подробную информацию об этой проблеме можно найти здесь

метод золотой спирали

Вы сказали, что не можете заставить метод золотой спирали работать, и это позор, потому что это очень, очень хорошо. Я хотел бы дать вам полное понимание этого, чтобы, возможно, вы могли понять, как удержать это от "сгущения"."

Итак, вот быстрый, неслучайный способ создания решетки, которая является приблизительно правильной; как обсуждалось выше, никакая решетка не будет идеальной, но это может быть "достаточно хорошо". Это по сравнению с другими методами, например, at BendWavy.org но он просто имеет приятный и красивый вид, а также гарантию о равномерном интервале в пределе.

праймер: спирали подсолнечника на диске блока

чтобы понять этот алгоритм, я сначала предлагаю вам посмотреть на 2D алгоритм спирали подсолнечника. Это основано на том, что самым иррациональным числом является золотое сечение (1 + sqrt(5))/2 и если один испускает точки по подходу " стоять в центре, поверните золотой соотношение целых витков, а затем испускают другую точку в этом направлении, " естественно, строит спираль, которая, как вы получаете все большее и большее количество точек, тем не менее отказывается иметь четко определенные "бары", что точки выстраиваются на.^{(Примечание 1.)}

алгоритм для равномерного интервала на диске,

from numpy import pi, cos, sin, sqrt, arange
import matplotlib.pyplot as pp

num_pts = 100
indices = arange(0, num_pts, dtype=float) + 0.5

r = sqrt(indices/num_pts)
theta = pi * (1 + 5**0.5) * indices

pp.scatter(r*cos(theta), r*sin(theta))
pp.show()

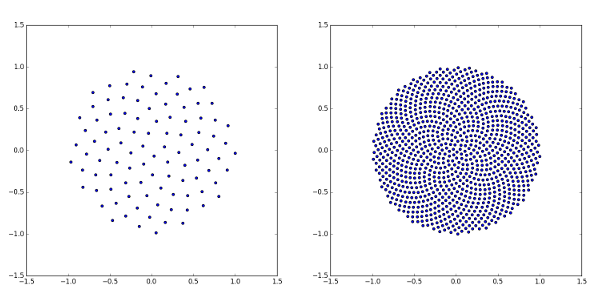
и он дает результаты, которые выглядят как (n=100 и n=1000):

интервал точки радиально

ключевой странной вещью является формула r = sqrt(indices / num_pts); как я дошел до этого? ^{(примечание 2.)}

Ну, я использую квадратный корень здесь, потому что я хочу, чтобы они имели четное пространство вокруг сферы. Это то же самое, что сказать, что в пределе большого N я хочу немного области R ∈ (r, r + dr), Θ ∈ (θ, θ + dθ), чтобы содержать количество точек, пропорциональных его площади, которая r dr dθ. Теперь, если мы притворимся, что мы говорим о случайной переменной здесь, это имеет простую интерпретацию, как говоря, что совместная плотность вероятности для (R, Θ) только c r для некоторой постоянной c. Нормализация на единичном диске затем заставляет c = 1/π.

теперь позвольте мне представить трюк. Она исходит из теории вероятностей, где он известен как выборка обратного CDF: предположим, вы хотели создать случайная величина с плотностью вероятности f(z) и у вас есть случайная величина U ~ Форма (0, 1), так же, как выходит из random() в большинстве языков программирования. Как ты это делаешь?

1. первый, превратите свою плотность в кумулятивная функция распределения F(z), который, помните, монотонно увеличивается от 0 до 1, где производное f(z).
2. затем вычислите обратную функцию CDF F^-1(z).
3. вы найдете, что Z = F^-1(U) распространяется по к целевой плотности. ^{(Примечание 3).}

теперь спираль золотого сечения трюк пространства указывает в красиво даже шаблон для θ Итак, давайте интегрируем это; для единичного круга мы остаемся с F(r) = r². Таким образом, обратная функция F^-1(u) = u^1/2, и поэтому мы хотели генерировать случайные точки На сфере в полярных координатах с r = sqrt(random()); theta = 2 * pi * random().

вместо случайно выборка этой обратной функции мы единообразно выборка, и хорошая вещь о равномерной выборке заключается в том, что наши результаты о том, как точки распределены в пределе больших N будет вести себя так, как будто мы произвольно выбрали его. Эта комбинация и есть фокус. Вместо random() мы используем:(arange(0, num_pts, dtype=float) + 0.5)/num_pts, так что, скажем, если мы хотим образец 10 очков они r = 0.05, 0.15, 0.25, ... 0.95. Мы равномерно выберем r чтобы получить интервал равной площади, и мы используем приращение подсолнечника, чтобы избежать ужасных "баров" точек на выходе.

Теперь делаем подсолнух на шаре

изменения, которые нам нужно сделать, чтобы усеять сферу точками, просто включают переключение полярных координат на сферические координаты. Радиальная координата, конечно, не входит в это, потому что мы находимся на единичной сфере. Чтобы держать вещи немного более последовательным здесь, хотя я был обучен как физик, я буду использовать координаты математиков, где 0 ≤ φ ≤ π-широта, сходящая с полюса, и 0 ≤ θ ≤ 2π-долгота. Таким образом, разница сверху заключается в том, что мы в основном заменяем переменную r с φ.

наш элемент области, который был r dr dθ, теперь становится не-намного-более-сложный грех (φ) dφ dθ. Так наша совместная плотность для равномерного дистанционирования грех (φ)/4π. Объединяя θ, мы находим f(φ) = грех(φ)/2,F(φ) = (1-cos (φ))/2. Инвертируя это, мы видим, что равномерная случайная величина будет выглядеть как acos (1 - 2 u), но мы пробуем равномерно вместо случайного, поэтому мы вместо этого используем φ_k = ЭКОСа(1 - 2 (k + 0.5)/N). И остальная часть алгоритма просто проецирует это на координаты x, y и z:

from numpy import pi, cos, sin, arccos, arange
import mpl_toolkits.mplot3d
import matplotlib.pyplot as pp

num_pts = 1000
indices = arange(0, num_pts, dtype=float) + 0.5

phi = arccos(1 - 2*indices/num_pts)
theta = pi * (1 + 5**0.5) * indices

x, y, z = cos(theta) * sin(phi), sin(theta) * sin(phi), cos(phi);

pp.figure().add_subplot(111, projection='3d').scatter(x, y, z);
pp.show()

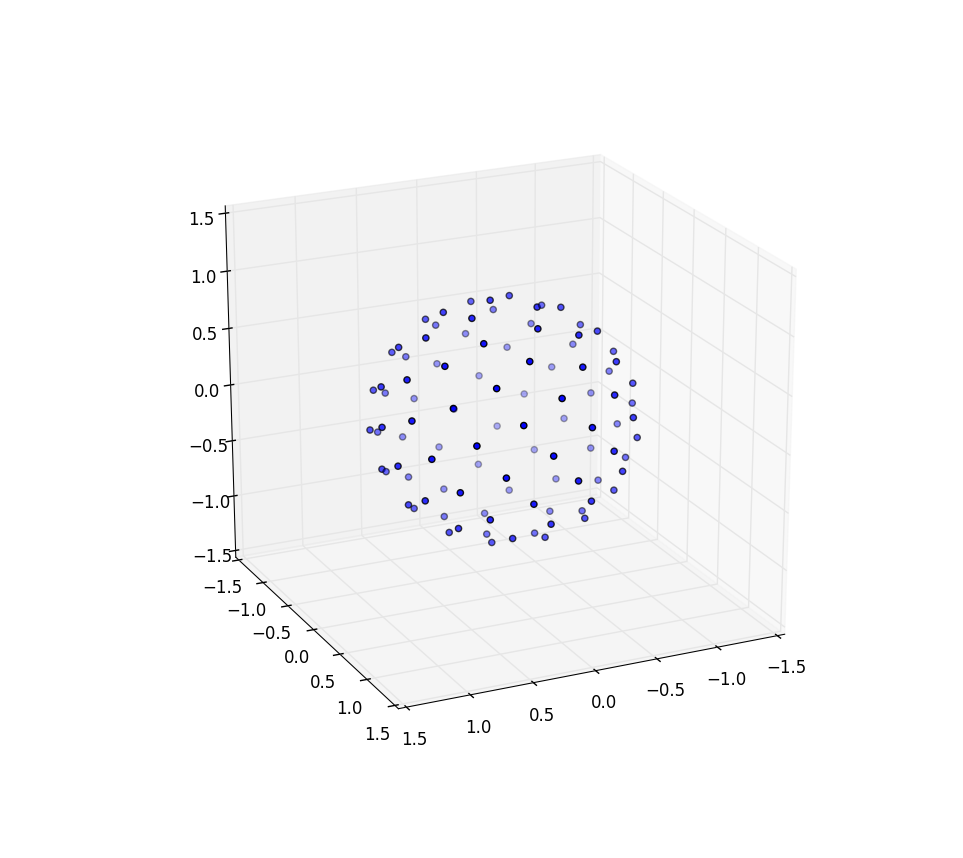
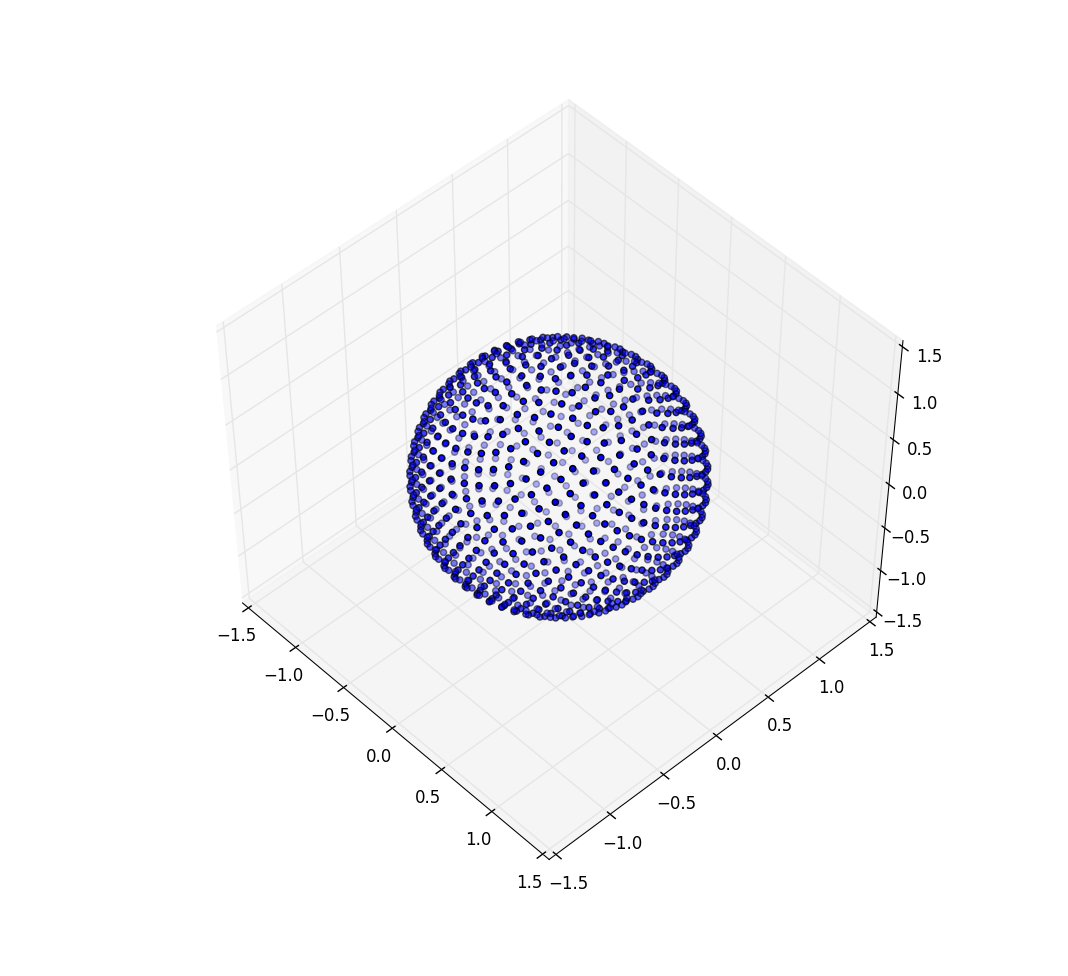
снова для n=100 и n=1000 результаты выглядят:

Примечания

1. эти "бары" сформированы рациональным приближения к числу, и лучшие рациональные приближения к числу происходят из его непрерывного выражения дроби,z + 1/(n_1 + 1/(n_2 + 1/(n_3 + ...))) здесь z является целым числом и n_1, n_2, n_3, ... - это конечная или бесконечная последовательность натуральных чисел:

   def continued_fraction(r):
       while r != 0:
           n = floor(r)
           yield n
           r = 1/(r - n)
   

   так как часть фракции 1/(...) всегда находится между нулем и единицей, большое целое число в непрерывной дроби допускает особенно хорошее рациональное приближение: "один, разделенный чем-то между 100 и 101", лучше, чем "один разделить что-то между 1 и 2."Поэтому самое иррациональное число-это то, которое 1 + 1/(1 + 1/(1 + ...)) и не имеет особо хороших рациональных приближений, можно решить φ = 1 + 1/φ умножить на φ чтобы получить формулу золотого сечения.

   1. для людей, которые не так хорошо знакомы с NumPy - все функции "векторизованы", так что sqrt(array) это то же самое, что и другие языки пиши map(sqrt, array). Так это покомпонентный sqrt приложение. То же самое относится и к делению скаляром или сложению скалярами-они применяются ко всем компонентам параллельно.

   2. доказательство простое, как только вы знаете, что это результат. Если вы спросите, какова вероятность того, что z Z z + dz, это то же самое, что спросить, какова вероятность того, что z F^-1(U)z + dz применить F ко всем трем выражениям, отмечая, что это монотонно возрастающая функция, следовательно F(z)U F(z + dz), разверните правую сторону, чтобы найти F(z) + f(z) dz, и с U однородна эта вероятность просто f(z) dz как и было обещано.

этот ответ основан на той же "теории", изложенной и ответ

Я добавляю этот ответ как:
-- Ни один из других вариантов не соответствует "однородности", нужно "пятно на" (или не очевидно-явно так). (Отмечая, чтобы получить планету, как распределение, выглядящее поведение, особенно желаемое в исходном ask, вы просто отклоняете из конечного списка K равномерно созданных точек случайным образом (random wrt Index count in the k items back).)
-- Ближайший другой impl заставил вас решить "N" по "угловой оси", а не только "одно значение N" по обоим значениям угловой оси (что при низких значениях N очень сложно узнать, что может, или может не иметь значения (например, вы хотите " 5 " точек-получайте удовольствие)))
-- Кроме того, очень трудно "grok", как различать другие варианты без каких-либо изображений, так что вот как выглядит этот вариант (ниже) и готовая к запуску реализация, которая идет с ним.

С N в 20:

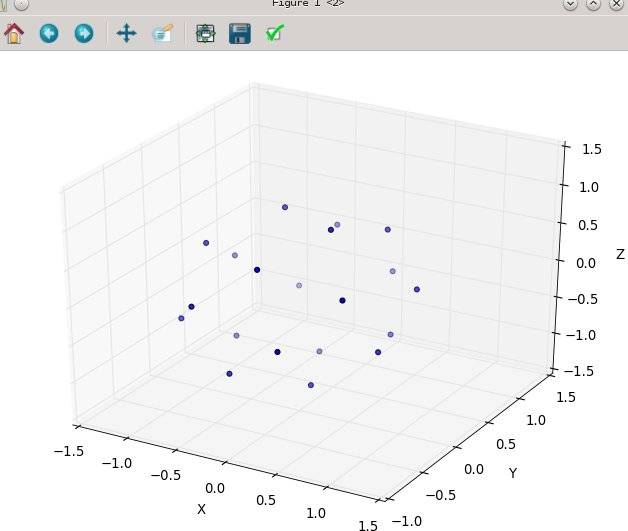
а потом N в 80:

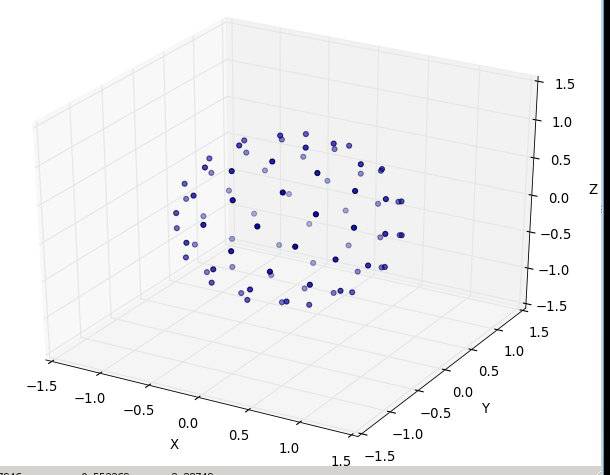
вот готовый к запуску код python3, где эмуляция является тем же самым источником:" http://web.archive.org/web/20120421191837/http://www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere "найдено другими. (Заговор, который я включил, который срабатывает при запуске как "главный", взят из: http://www.scipy.org/Cookbook/Matplotlib/mplot3D )

from math import cos, sin, pi, sqrt

def GetPointsEquiAngularlyDistancedOnSphere(numberOfPoints=45):
    """ each point you get will be of form 'x, y, z'; in cartesian coordinates
        eg. the 'l2 distance' from the origion [0., 0., 0.] for each point will be 1.0 
        ------------
        converted from:  http://web.archive.org/web/20120421191837/http://www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere ) 
    """
    dlong = pi*(3.0-sqrt(5.0))  # ~2.39996323 
    dz   =  2.0/numberOfPoints
    long =  0.0
    z    =  1.0 - dz/2.0
    ptsOnSphere =[]
    for k in range( 0, numberOfPoints): 
        r    = sqrt(1.0-z*z)
        ptNew = (cos(long)*r, sin(long)*r, z)
        ptsOnSphere.append( ptNew )
        z    = z - dz
        long = long + dlong
    return ptsOnSphere

if __name__ == '__main__':                
    ptsOnSphere = GetPointsEquiAngularlyDistancedOnSphere( 80)    

    #toggle True/False to print them
    if( True ):    
        for pt in ptsOnSphere:  print( pt)

    #toggle True/False to plot them
    if(True):
        from numpy import *
        import pylab as p
        import mpl_toolkits.mplot3d.axes3d as p3

        fig=p.figure()
        ax = p3.Axes3D(fig)

        x_s=[];y_s=[]; z_s=[]

        for pt in ptsOnSphere:
            x_s.append( pt[0]); y_s.append( pt[1]); z_s.append( pt[2])

        ax.scatter3D( array( x_s), array( y_s), array( z_s) )                
        ax.set_xlabel('X'); ax.set_ylabel('Y'); ax.set_zlabel('Z')
        p.show()
        #end

проверено при низких подсчетах (N в 2, 5, 7, 13 и т. д.) и, похоже, работает "хорошо"

то, что вы ищете называется сферическая покрытие. Задача сферического покрытия очень сложна, и решения неизвестны, за исключением небольшого числа точек. Одно известно наверняка, что при n точках на сфере всегда существуют две точки расстояния d = (4-csc^2(\pi n/6(n-2)))^(1/2) или ближе.

если вы хотите вероятностный метод для генерации точек, равномерно распределенных на сфере, это легко: генерировать точки в пространстве равномерно гауссовым дистрибутив (он встроен в Java, не сложно найти код для других языков). Так что в 3-мерном пространстве, нужно что-то вроде

Random r = new Random();
double[] p = { r.nextGaussian(), r.nextGaussian(), r.nextGaussian() };

затем проецируйте точку на сферу, нормализуя ее расстояние от начала координат

double norm = Math.sqrt( (p[0])^2 + (p[1])^2 + (p[2])^2 ); 
double[] sphereRandomPoint = { p[0]/norm, p[1]/norm, p[2]/norm };

гауссово распределение в N измерениях сферически симметрично, поэтому проекция на сферу равномерна.

конечно, нет никакой гарантии, что расстояние между любыми двумя точками в коллекцию равномерно сгенерированные точки будут ограничены ниже, поэтому вы можете использовать отклонение для выполнения любых таких условий, которые у вас могут быть: вероятно, лучше всего создать всю коллекцию, а затем при необходимости отклонить всю коллекцию. (Или используйте "раннее отклонение", чтобы отклонить всю коллекцию, которую вы создали до сих пор; просто не сохраняйте некоторые моменты и не отбрасывайте другие.) Вы можете использовать формулу для d учитывая выше, минус некоторая слабина, чтобы определить минимальное расстояние между точками, ниже которых вы будете отклонять набор точек. Вам нужно будет рассчитать n выбрать 2 расстояния, и вероятность отклонения будет зависеть от слабины; трудно сказать, Как, поэтому запустите симуляцию, чтобы почувствовать соответствующую статистику.

попробуй:

function sphere ( N:float,k:int):Vector3 {
    var inc =  Mathf.PI  * (3 - Mathf.Sqrt(5));
    var off = 2 / N;
    var y = k * off - 1 + (off / 2);
    var r = Mathf.Sqrt(1 - y*y);
    var phi = k * inc;
    return Vector3((Mathf.Cos(phi)*r), y, Mathf.Sin(phi)*r); 
};

вышеуказанная функция должна работать в цикле с общей петлей N и текущей итерацией цикла k.

Он основан на картине семян подсолнечника, за исключением того, что семена подсолнечника изогнуты вокруг в половину купола и снова в сферу.

вот изображение, за исключением того, что я помещаю камеру на полпути внутри сферы, поэтому она выглядит 2d вместо 3d, потому что камера находится на одинаковом расстоянии от всех точки. http://3.bp.blogspot.com/-9lbPHLccQHA/USXf88_bvVI/AAAAAAAAADY/j7qhQsSZsA8/s640/sphere.jpg

с небольшим количеством точек вы можете запустить моделирование:

from random import random,randint
r = 10
n = 20
best_closest_d = 0
best_points = []
points = [(r,0,0) for i in range(n)]
for simulation in range(10000):
    x = random()*r
    y = random()*r
    z = r-(x**2+y**2)**0.5
    if randint(0,1):
        x = -x
    if randint(0,1):
        y = -y
    if randint(0,1):
        z = -z
    closest_dist = (2*r)**2
    closest_index = None
    for i in range(n):
        for j in range(n):
            if i==j:
                continue
            p1,p2 = points[i],points[j]
            x1,y1,z1 = p1
            x2,y2,z2 = p2
            d = (x1-x2)**2+(y1-y2)**2+(z1-z2)**2
            if d < closest_dist:
                closest_dist = d
                closest_index = i
    if simulation % 100 == 0:
        print simulation,closest_dist
    if closest_dist > best_closest_d:
        best_closest_d = closest_dist
        best_points = points[:]
    points[closest_index]=(x,y,z)


print best_points
>>> best_points
[(9.921692138442777, -9.930808529773849, 4.037839326088124),
 (5.141893371460546, 1.7274947332807744, -4.575674650522637),
 (-4.917695758662436, -1.090127967097737, -4.9629263893193745),
 (3.6164803265540666, 7.004158551438312, -2.1172868271109184),
 (-9.550655088997003, -9.580386054762917, 3.5277052594769422),
 (-0.062238110294250415, 6.803105171979587, 3.1966101417463655),
 (-9.600996012203195, 9.488067284474834, -3.498242301168819),
 (-8.601522086624803, 4.519484132245867, -0.2834204048792728),
 (-1.1198210500791472, -2.2916581379035694, 7.44937337008726),
 (7.981831370440529, 8.539378431788634, 1.6889099589074377),
 (0.513546008372332, -2.974333486904779, -6.981657873262494),
 (-4.13615438946178, -6.707488383678717, 2.1197605651446807),
 (2.2859494919024326, -8.14336582650039, 1.5418694699275672),
 (-7.241410895247996, 9.907335206038226, 2.271647103735541),
 (-9.433349952523232, -7.999106443463781, -2.3682575660694347),
 (3.704772125650199, 1.0526567864085812, 6.148581714099761),
 (-3.5710511242327048, 5.512552040316693, -3.4318468250897647),
 (-7.483466337225052, -1.506434920354559, 2.36641535124918),
 (7.73363824231576, -8.460241422163824, -1.4623228616326003),
 (10, 0, 0)]

Возьмите два самых больших фактора вашего N, если N==20 тогда два самых больших фактора {5,4}, или, в более общем смысле {a,b}. Вычислить

dlat  = 180/(a+1)
dlong = 360/(b+1})

поставьте свою первую точку на {90-dlat/2,(dlong/2)-180}, второй на {90-dlat/2,(3*dlong/2)-180}, ваш 3-й в {90-dlat/2,(5*dlong/2)-180}, пока вы не споткнулись Вокруг света один раз, к этому времени вы должны около {75,150} когда вы идете рядом с {90-3*dlat/2,(dlong/2)-180}.

очевидно, я работаю над этим в градусах на поверхности сферической земли, с обычным соглашения для перевода + /-в N/S или E / W. И, очевидно, это дает вам совершенно неслучайное распределение, но оно однородно, и точки не сгруппированы вместе.

чтобы добавить некоторую степень случайности, вы можете создать 2 нормально распределенных (со средним 0 и std dev {dlat/3, dlong/3} соответственно) и добавить их в равномерно распределенные точки.

edit: это не отвечает на вопрос, который ОП хотел задать, оставив его здесь, если люди найдут его полезным.

мы используем правило умножения вероятностей, в сочетании с infinitessimals. Это приводит к 2 строкам кода для достижения желаемого результата:

longitude: φ = uniform([0,2pi))
azimuth:   θ = -arcsin(1 - 2*uniform([0,1]))

(определены в следующей системе координат:)

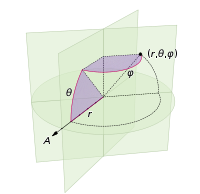
ваш язык обычно имеет однородный примитив случайных чисел. Для пример в Python вы можете использовать random.random() чтобы вернуть число в диапазоне [0,1). Вы можете умножить это число на K, чтобы получить случайное число в диапазоне [0,k). Таким образом, в Python uniform([0,2pi)) означает random.random()*2*math.pi.

доказательство

теперь мы не можем назначить uniformly равномерно, иначе мы бы получили сгустки на полюсах. Мы хотим назначить вероятности, пропорциональные площади поверхности сферического клина (θ на этой диаграмме фактически φ):

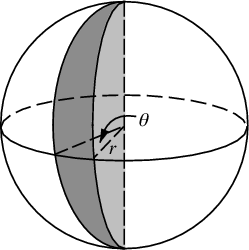
угловое смещение dφ на экваторе приведет к смещению dφ*R. Каким будет это смещение при произвольном Азимуте θ? Ну, радиус от оси z равен r*sin(θ), таким образом, длина дуги этой "широты", пересекающей клин, равна dφ * r*sin(θ). Таким образом мы вычисляем распределение области для того чтобы попробовать от его, путем интегрировать зону отрезка от южного полюса к северу полюс.

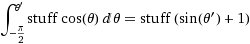(где stuff=dφ*r)

теперь мы попытаемся получить обратный CDF для выборки из него:http://en.wikipedia.org/wiki/Inverse_transform_sampling

Сначала мы нормализуем, разделив наш почти CDF на его максимальное значение. Это имеет побочный эффект отмены dφ и r.

azimuthalCDF: cumProb = (sin(θ)+1)/2 from -pi/2 to pi/2

inverseCDF: θ = -sin^(-1)(1 - 2*cumProb)

таким образом:

let x by a random float in range [0,1]
θ = -arcsin(1-2*x)

или... разместить на 20 пунктов, вычислительных центров icosahedronal лица. Для 12 точек найдите вершины икосаэдра. Для 30 точек-средняя точка ребер икосаэдра. вы можете сделать то же самое с тетраэдром, кубом, додекаэдром и октаэдрами: один набор точек находится на вершинах, другой-в центре Грани, а другой-в центре ребер. Однако их нельзя смешивать.

Healpix решает тесно связанную проблему (пикселизация сферы с пикселями равной площади):

http://healpix.sourceforge.net/

Это, вероятно, перебор, но, возможно, посмотрев на него, вы поймете, что некоторые из его других хороших свойств интересны вам. Это больше, чем просто функция, которая выводит облако точек.

Я приземлился здесь, пытаясь найти его снова; название "healpix" точно не вызывает сфер...

# create uniform spiral grid
numOfPoints = varargin[0]
vxyz = zeros((numOfPoints,3),dtype=float)
sq0 = 0.00033333333**2
sq2 = 0.9999998**2
sumsq = 2*sq0 + sq2
vxyz[numOfPoints -1] = array([(sqrt(sq0/sumsq)), 
                              (sqrt(sq0/sumsq)), 
                              (-sqrt(sq2/sumsq))])
vxyz[0] = -vxyz[numOfPoints -1] 
phi2 = sqrt(5)*0.5 + 2.5
rootCnt = sqrt(numOfPoints)
prevLongitude = 0
for index in arange(1, (numOfPoints -1), 1, dtype=float):
  zInc = (2*index)/(numOfPoints) -1
  radius = sqrt(1-zInc**2)

  longitude = phi2/(rootCnt*radius)
  longitude = longitude + prevLongitude
  while (longitude > 2*pi): 
    longitude = longitude - 2*pi

  prevLongitude = longitude
  if (longitude > pi):
    longitude = longitude - 2*pi

  latitude = arccos(zInc) - pi/2
  vxyz[index] = array([ (cos(latitude) * cos(longitude)) ,
                        (cos(latitude) * sin(longitude)), 
                        sin(latitude)])

это работает и это смертельно просто. Столько очков, сколько вы хотите:

    private function moveTweets():void {


        var newScale:Number=Scale(meshes.length,50,500,6,2);
        trace("new scale:"+newScale);


        var l:Number=this.meshes.length;
        var tweetMeshInstance:TweetMesh;
        var destx:Number;
        var desty:Number;
        var destz:Number;
        for (var i:Number=0;i<this.meshes.length;i++){

            tweetMeshInstance=meshes[i];

            var phi:Number = Math.acos( -1 + ( 2 * i ) / l );
            var theta:Number = Math.sqrt( l * Math.PI ) * phi;

            tweetMeshInstance.origX = (sphereRadius+5) * Math.cos( theta ) * Math.sin( phi );
            tweetMeshInstance.origY= (sphereRadius+5) * Math.sin( theta ) * Math.sin( phi );
            tweetMeshInstance.origZ = (sphereRadius+5) * Math.cos( phi );

            destx=sphereRadius * Math.cos( theta ) * Math.sin( phi );
            desty=sphereRadius * Math.sin( theta ) * Math.sin( phi );
            destz=sphereRadius * Math.cos( phi );

            tweetMeshInstance.lookAt(new Vector3D());


            TweenMax.to(tweetMeshInstance, 1, {scaleX:newScale,scaleY:newScale,x:destx,y:desty,z:destz,onUpdate:onLookAtTween, onUpdateParams:[tweetMeshInstance]});

        }

    }
    private function onLookAtTween(theMesh:TweetMesh):void {
        theMesh.lookAt(new Vector3D());
    }