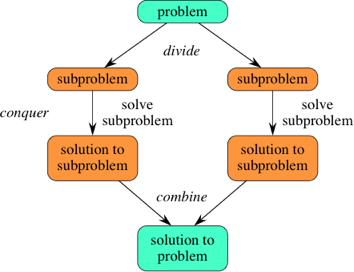
разделяй и властвуй, рекурсия.
интересно, всегда ли техника "разделяй и властвуй" делит проблему на подзадачи одного типа? Под тем же типом я имею в виду, что его можно реализовать с помощью функции с рекурсией. Может ли divide и conquer всегда реализовываться рекурсией?
спасибо!
7 ответов
"всегда" -страшное слово, но я не могу придумать ситуацию "разделяй и властвуй", в которой вы не могли бы использовать рекурсию. Именно по определению "разделяй и властвуй" создает подзадачи той же формы, что и исходная задача - эти подзадачи постоянно разбиваются до тех пор, пока не будет достигнут некоторый базовый случай, и количество делений коррелирует с размером входных данных. Рекурсия-естественный выбор для такого рода проблем.
посмотреть статья в Википедии для больше хорошей информации.
Как правило, да! сортировка слиянием пример то же самое. Вот это анимационная версия то же самое.
да. В алгоритмической технике "разделяй и властвуй" мы разделяем данную большую задачу на более мелкие подзадачи. Эти меньшие подзадачи должны быть похожи на большую проблему, за исключением того, что они меньше по размеру.
например, задача сортировки массива размера N ничем не отличается от задачи сортировки массива размера N/2. За исключением того, что последний размер проблемы меньше, чем у предыдущего.
Если меньшая подзадача не похожа на чем больше, тем техника "разделяй и властвуй" не может быть использована для решения большей проблемы. Другими словами, данная проблема может быть решена с помощью техники "разделяй и властвуй", только если данная большая проблема может быть разделена на меньшие подзадачи, которые похожи на большую проблему.
изучение алгоритма сортировки слиянием будет достаточно для этого вопроса. После понимания реализации алгоритма сортировки слиянием с помощью divide and conquer (также рекурсия) вы увидите, насколько сложно было бы сделать это без рекурсии.
на самом деле самое главное здесь-сложность алгоритма, который выражается с помощью нотации big-oh и nlogn для сортировки слияния.
для mergesort exapmle есть другая версия, которая называется снизу вверх объединить сортировку. Это простая и нерекурсивная его версия.
Это примерно на 10% медленнее, чем рекурсивные, нисходящие слияния в типичных системах. Вы можете обратиться к следующей ссылке для получения дополнительной информации. Это хорошо объясняется в 3-й лекции.
Рекурсия-это метод программирования, в котором вы определяете функцию в терминах самой себя. Функция обычно вызывает себя со слегка измененными параметрами (для сходимости).
- разделите проблему на две или более мелкие подзадачи.
- победить подзадачи, решая их (рекурсивно).
- объединить решения подзадач в решение исходной задачи.
Да все Divide и Conquer всегда реализуются с помощью рекурсии .
типичный алгоритм Divide and Conquer решает проблему, используя следующие три шага.
- разделить: разбить данную проблему на подзадачи одного типа.
- Conquer: рекурсивно решить эти подзадачи
- объединить: правильно сочетать ответы
Ниже приведены некоторые стандартные алгоритмы, которые разделяют и покоряют алгоритмы. 1) бинарный поиск, 2) Быстрая Сортировка, 3) Сортировка Слиянием, 4) алгоритм Штрассена