Разница между гамильтоновым путем и путем Эйлера
может ли кто-нибудь сказать мне разницу между гамильтоновым путем и путем Эйлера. Они похожи!
8 ответов
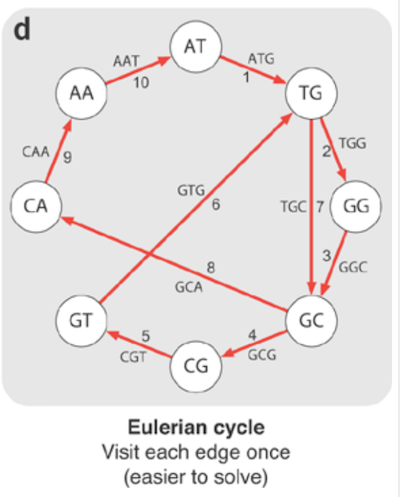
An Эйлеров путь - это путь, который пересекает каждое ребро ровно один раз без повторения, если он заканчивается в начальной вершине, то это цикл Эйлера.
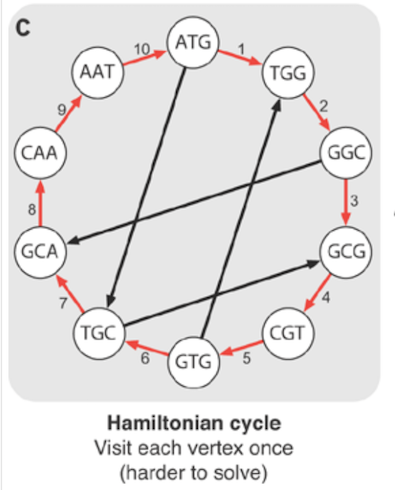
A путь гамильтониана проходит через каждую вершину (обратите внимание не на каждое ребро), ровно один раз, если она заканчивается в начальной вершине, то это Гамильтонов цикл.
в пути Эйлера вы можете пройти через вершину более одного раза.
в Гамильтоновом пути вы не можете пройти через все стыки.
Эйлеров путь должен посетить каждый edge ровно один раз, в то время как Гамильтонов путь должен посетить каждый вершинный ровно один раз.
Определения Теории Графов
(в порядке убывания общности)
прогулка: последовательность ребер, где конец одного ребра обозначает начало следующего ребра
след: прогулка, которая не повторяет ни края. Все тропы-это тропы.
путь: прогулка, где каждая вершина проходит ровно один раз. (пути, используемые для ссылки на open теперь определение изменилось) свойство пересечения вершин только один раз означает, что ребра также пересекаются только один раз, поэтому все пути являются тропами.
Гамильтоновы пути и эйлеровы тропы
путь гамильтониана посещение каждая вершина в графе (ровно один раз, потому что это путь)
Эйлера след посещение каждое ребро в графе ровно один раз (поскольку это тропа, вершины вполне могут пересекаться не один раз.)
Гамильтонов путь посещает каждый узел (или вершину) ровно один раз, а Эйлеров путь пересекает каждое ребро ровно один раз.
Они связаны, но не являются ни зависимыми, ни взаимоисключающими. Если граф имеет цикл Эурлера, он может или не может также иметь Гамильтонов циль и наоборот.
циклы Эйлера посетить каждый edge в графа ровно один раз. Если в графе есть вершины с более чем двумя ребрами, то по определению цикл будет проходить через эти вершины не один раз. В результате вершины могут повторяться, но ребра не может.
Гамильтоновы циклы посетить каждый вершинный на графике ровно один раз (аналогично проблеме коммивояжера). В результате ни ребра, ни вершины не могут быть повторены.
Я буду использовать общий пример в биологии; реконструкция генома путем создания образцов ДНК.
de-novo assembly
чтобы построить геном из коротких считываний, необходимо построить график этих считываний. Мы делаем это, разбивая считывания на k-мер и собирая их в график.
мы можем восстановить геном, посетив каждый узел один раз, как на диаграмме. Это известно как гамильтониан путь.
к сожалению, построение такого пути NP-сложно. Невозможно вывести эффективный алгоритм его решения. Вместо этого в биоинформатике мы строим Эйлеров цикл, где ребро представляет собой перекрытие.
путь Эйлера-это путь, который использует каждый край графа ровно один раз.и у него должно быть ровно две нечетные вершины.путь начинается и заканчивается в другой вершине. Гамильтонов цикл-это цикл, содержащий каждую вершину графа, поэтому вы не можете использовать все ребра графа.
путь Эйлера-это граф, использующий каждое ребро (Примечание) графа только один раз. Схема Эйлера-это путь Эйлера, который возвращает ему начальную точку после покрытия всех краев.
в то время как путь Гамильтона-это граф, который охватывает все вершины(Примечание) ровно один раз. Когда этот путь возвращается к своей начальной точке, этот путь называется цепью Гамильтона.