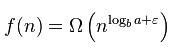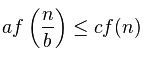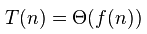Решить: T (n) = T (n/2) + n / 2 + 1

Я изо всех сил пытаюсь определить время работы для следующего алгоритма в нотации O. Мое первое предположение было O (n), но разрыв между итерациями и числом, которое я применяю, не является устойчивым. Как я неправильно определил это? 

public int function (int n ) 
{
  if ( n == 0) {
    return 0;
  }

  int i = 1;
  int j = n ;
  while ( i < j ) 
  {
    i = i + 1;
    j = j - 1;
  }
  return function ( i - 1) + 1;
}
13
asymptotic-complexity computer-science computer-science-theory time-complexity

2 ответов

на while выполняется примерно в n/2 времени.

рекурсия выполняется как передает n значение, которое составляет около половины исходного n, так:

n/2 (first iteration)
n/4 (second iteration, equal to (n/2)/2)
n/8
n/16
n/32
...

это похоже на геометрическая серия.

Infact его можно представить как 

n * (1/2 + 1/4 + 1/8 + 1/16 + ...)

таким образом, он сходится к n * 1 = n

таким образом, обозначение O O (n)

29

другой подход-записать его как T(n) = T(n/2) + n/2 + 1.
Время цикла n/2 работа. Спор перешел в следующий призыв n/2.

решение этого с помощью мастер теореме где:

  • a = 1
  • b = 2
  • f = n / 2 + 1

enter image description here

enter image description here

Let c=0.9
1*(f(n/2) + 1) <? c*f(n)
1*(n/4)+1 <? 0.9*(n/2 + 1)
0.25n + 1 <? 0.45n + 0.9
     0    <  0.2n - 0.1

enter image description here

что есть:

T(n) = Θ(n)
5