Реверсивный генератор псевдослучайных последовательностей
Я хотел бы какой-то метод для создания довольно длинная последовательность случайных чисел что я могу пролистывать вперед и назад. Как машина с кнопками" next "и" previous", которая даст вам случайные числа.
что-то вроде 10-битного разрешения (т. е. положительных целых чисел в диапазоне от 0 до 1023) достаточно, и последовательность >100k чисел. Это для простого приложения типа игры,мне не нужна сила шифрования случайность или что-нибудь, но я хочу, чтобы это было довольно случайным. У меня есть ограниченный объем памяти доступно, поэтому я не могу просто генерировать кусок случайных данных и проходить через него. Мне нужно получить номера в "интерактивном времени" - я могу легко потратить несколько МС, думая о следующем номере, но не намного больше. В конце концов он будет работать на каком-то микроконтроллере, возможно, просто Arduino.
Я мог бы сделать это с простой линейной конгруэнтный генератор (LCG). Идти вперед просто, чтобы вернуться назад, я должен был бы кэшировать самые последние числа и хранить некоторые точки с интервалами, чтобы я мог воссоздать последовательность оттуда.
но, может быть, есть какой-то псевдослучайный генератор, который позволяет идти вперед и вперед? Должно быть возможно подключить два линейных регистра сдвига обратной связи (LFSRs), чтобы катиться в разных направлениях, нет?
или, может быть, я могу просто пройти с искажением номера индекса используя какую-то хэш-функцию? Сначала я попробую.
есть другие идеи?
7 ответов
попросил очень похожий вопрос на форумах tigsource.
хеширования
по крайней мере в играх, хэш-функция, вероятно, может делать то, что вы хотите. Вы могли бы сделать это так
class ReversibleRNG {
int x;
public:
ReversibleRNG(int seed) : x(seed) {}
int next(){return yourFavoriteHash(++x);}
int prev(){return yourFavoriteHash(--x);}
};
реверсивный линейный конгруэнтный генератор (lcg)
как указали несколько человек, lcg действительно обратим. В lcg следующее состояние вычисляется следующим образом:
x = (a * prevx + c) mod m
мы можем изменить это:
x ≡ a * prevx + c (mod m)
x - c ≡ a * prevx (mod m)
поскольку a и m выбраны относительно простыми в lcg, мы можем найти обратное, используя алгоритм расширенного Евклида.
ainverse = extEuclid(a, m).x;
ainverse * (x - c) ≡ ainverse * a * prevx (mod m)
ainverse * (x - c) ≡ prevx (mod m)
что означает
prevx = ainverse * (x - c) mod m
если вы выбираете M и тщательно, алгоритм может иметь период 2^64
реализация
Я заголовок-только реализация этого алгоритма на случай, если кто-то заинтересован.
используя очень простой симметричный алгоритм шифрования является одним из самых простых способов сделать это. Каждое случайное число формируется просто зашифровать предыдущий с некоторым фиксированным ключом и идти назад вы просто расшифровать.
вы можете посмотреть на RC4-код вhttp://en.wikipedia.org/wiki/RC4. Вы можете использовать гораздо меньший ключевой график, чтобы все это поместилось на arduino.
зашифровать последовательность 1, 2, 3, ... с любым шифром и любым ключом.
AES доступен практически на каждой последней системе, и это молнии быстро.
просто обратный порядок битов в возрастающей последовательности целых чисел. Например (с разрешением 8 бит):
- 0 0
- 1 128
- 2 64
- 3 192
- 4 32
- etc
очень легко двигаться вперед и назад в последовательности и намного быстрее, чем вызов шифрования или хэш-функций. Оно также имеет преимущество производить самое длинн-возможное последовательность.
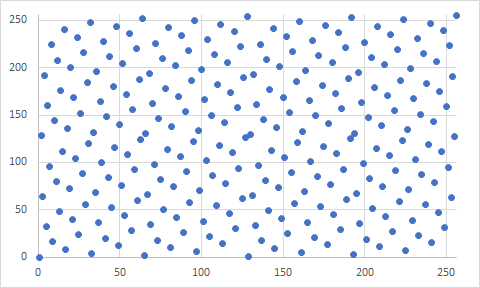
Это определенно не криптографически-защищенные. Вот диаграмма разброса сгенерированных значений (опять же с 8-битным разрешением):
вы можете легко видеть шаблоны, хотя это может быть "случайным" достаточно для вас.
Если линейный конгруэнтный генератор достаточно хорош, используйте его. Они легко обратимы. Дело в том, что обратный генератор также является LCG. LCGs может также пропустить в любом направлении (вперед и назад) очень быстро.
подробности можно найти в искусство компьютерного программирования-Том 2
в частности, раздел 3.2.1 Страница 10 уравнения 6-8 TAOCP, а также Упражнение 5 дают желаемые результаты. В случае, если вы не можете решить упражнение, вы можете найти решение легко, например,здесь
хотя я согласен с @BlueRaja, что вы должны просто использовать AES в "встречном режиме", со случайным или временным запуском для вашей последовательности, AES может быть недоступен или невозможен в вашей встроенной ситуации.
Я нашел эта интересная статья это обсуждает, как построить обратимый PRNG; это всего лишь 10 страниц и имеет много образцов кода. Дайте это попробовать, если AES не работает для вас.
вы также можете вернуться назад с LCG, это просто еще один LCG, используя обратный множитель по модулю модуля вместе с подходящим приращением.
для ваших небольших чисел вы можете просто использовать грубую силу для поиска обратного, в общем случае его можно вычислить с помощью расширенного алгоритма GCD.
Если ваша игра строго для удовольствия, без каких-либо ставок, я бы выбрал что-то криптографически безопасное, например подход AES предложенный другими. LCGs и другие линейные генераторы случайных чисел не могут противостоять интеллектуальному противнику.