Рисовать сплайны с помощью Direct2D
у меня есть данные сплайновой кривой
- градусов
- узлы
- контрольных точек
- Fit points
и мне нужно нарисовать эту кривую, используя Direct2D. На данный момент я использую ID2D1GeometrySink интерфейс рисовать геометрию, но, похоже, она не реализует возможный AddSpline метод.
есть ли способ нарисовать сплайн с помощью Direct2D? Даже DirectX реализации, что может использоваться в теги Direct2D приложение будет хорошо.
3 ответов
Если у вас уже нет рабочего кода для основных операций NURBS или вы являетесь экспертом NURBS, я бы посоветовал использовать некоторую библиотеку NURBS. Как правило, набор операций, связанных с вашей проблемой:оценки, вставки узла, разделение, а может повышение степени.
для общности я опишу три возможных решения.
разделить на узлы
предположим, что ваш вклад Кривые NURBS нерациональны (без весов = единичные веса), и их степень не может превышать максимально допустимую степень результирующих кривых Безье. Тогда каждый промежуток сплайна является полиномиальной кривой, поэтому его можно извлечь как кривую Безье.
в зависимости от используемой библиотеки описание алгоритма может быть различным. Вот возможные варианты:
- если есть функция для разделения кривой NURBS на кривые Безье, просто вызовите он.
- предположим, что есть функция для разбиения кривой на две subcurves по данному параметру. Затем разделите кривую на любой внутренний узел (т. е. не равный min/max узлам). Сделайте то же самое для каждой из подкормок, пока не будет внутренних узлов, что означает, что все кривые Безье.
- любая библиотека NURBS должна иметь функцию вставки узла. Для каждого узла Ki с кратностью меньше D (степени) вызовите вставку узла с параметром = Ki. Вы можете вставить разные узлы в любом порядке. Библиотека также может содержать "множественную вставку узлов", что позволяет объединить все вставки в один вызов. В конце концов, узлы min/max должны иметь кратность D+1, все внутренние узлы должны иметь кратность D. В этот момент контрольные точки полностью описывают нужные вам кривые Безье: контрольные точки [0..D] определите 0-й Безье, [D..2D] определите 1-й Безье,..., [д-д .. (q+1) D] контрольные точки определяют q-й Безье.
Если степень ваша входная кривая NURBS ниже требуемой степени кривых Безье, вы также можете вызвать высоту степени либо для исходной кривой NURBS, либо для результирующих кривых Безье. Говоря об ID2D1GeometrySink, он принимает все кривые Безье со степенью
Если ваша кривая NURBS может иметь неприемлемо высокую степень или может быть рациональной, то вам нужно аппроксимировать кривую либо кубическим сплайном (сложнее и быстрее) или с полилинией (проще, но медленнее).
гарантированное приближение полилинии
вот довольно простой рекурсивный алгоритм, который строит полилинейную аппроксимацию кривой NURBS с гарантированной ошибкой
- нарисуйте отрезок линии от первой до последней контрольной точки кривой.
- Проверьте, находятся ли все контрольные точки на расстоянии MaxErr от сегмента.
- если они, то добавьте сегмент линии к выходу.
- в противном случае разделите кривую посередине на две подпространства и приблизьте их рекурсивно.
чтобы реализовать его, вам нужна операция расщепления кривой NURBS (которая может быть реализована с помощью вставки узла).
эвристическое приближение полилинии
если нет библиотеки NURBS под рукой, реализация вставки узла может вызвать много боли. Вот почему я описываю еще одно решение, которое использует только point оценка кривых NURBS. Вы можете реализовать оценку точки либо с помощью алгоритма de Boor, либо по определению (см. базисные функции и кривая NURBS определения)
алгоритм рекурсивен, он принимает параметрический интервал на исходной кривой в качестве входных данных.
- оценить начальную и конечную точки параметрического интервала.
- нарисуйте сегмент линии через них.
- оцените некоторое количество точки На кривой, внутри параметрического интервала.
- убедитесь, что эти внутренние точки находятся на расстоянии MaxErr от сегмента линии.
- если они есть, то добавьте сегмент линии к выходу.
- в противном случае разбейте параметрический интервал на две половины и вызовите аппроксимацию на них рекурсивно.
этот алгоритм адаптивен, и он может производить плохое приближение на практике в некоторых редких случаях. Контрольные точки можно выбрать равномерно в пределах параметрического интервала. Для большей надежности лучше также оценить кривую на всех узлах входной кривой, которые попадают в параметрический интервал.
сторонняя библиотека
Если вы не собираетесь много работать с NURBS, я предлагаю взять tinyspline библиотека. Он очень мал по дизайну, не имеет зависимостей и имеет лицензию MIT. Кроме того, он, кажется, активно развивается, поэтому вы можете общаться с автором в случае каких-либо проблем.
Кажется, что первого решения достаточно для стартера темы, поэтому вот код для разбиения NURBS на кривые Безье с tinyspline:
#include <stdlib.h>
#include <stdio.h>
#include <assert.h>
#include <math.h>
#include "tinysplinecpp.h"
#include "debugging.h"
int main() {
//create B-spline curve and set its data
TsBSpline nurbs(3, 2, 10, TS_NONE);
float knotsData[] = {0.0f, 0.0f, 0.0f, 0.0f, 0.3f, 0.3f, 0.5f, 0.7f, 0.7f, 0.7f, 1.0f, 1.0f, 1.0f, 1.0f};
for (int i = 0; i < nurbs.nKnots(); i++)
nurbs.knots()[i] = knotsData[i];
for (int i = 0; i < nurbs.nCtrlp(); i++) {
nurbs.ctrlp()[2*i+0] = 0.0f + i;
float x = 1.0f - i / float(nurbs.nCtrlp());
nurbs.ctrlp()[2*i+1] = x * x * x;
}
ts_bspline_print(nurbs.data());
//insert knots into B-spline so that it becomes a sequence of bezier curves
TsBSpline beziers = nurbs;
beziers.toBeziers();
ts_bspline_print(beziers.data());
//check that the library does not fail us
for (int i = 0; i < 10000; i++) {
float t = float(rand()) / RAND_MAX;
float *pRes1 = nurbs(t).result();
float *pRes2 = beziers(t).result();
float diff = hypotf(pRes1[0] - pRes2[0], pRes1[1] - pRes2[1]);
if (diff >= 1e-6f)
printf("Bad eval at %f: err = %f (%f;%f) vs (%f;%f)\n", t, diff, pRes1[0], pRes1[1], pRes2[0], pRes2[1]);
}
//extract bezier curves
assert(beziers.nCtrlp() % nurbs.order() == 0);
int n = beziers.nCtrlp() / nurbs.order();
int sz = nurbs.order() * 2; //floats per bezier
for (int i = 0; i < n; i++) {
float *begin = beziers.ctrlp() + sz * i;
float *end = beziers.ctrlp() + sz * (i + 1);
//[begin..end) contains control points of i-th bezier curve
}
return 0;
}
Конечная нота
большая часть текста выше предполагает, что ваши кривые NURBS являются зажимается, что означает, что узлы min и max имеют кратность D+1. Unclamped кривые NURBS также использованы иногда. Если вы встретите одного, Вам также может понадобиться зажмите его, используя функцию approproate библиотеки. Метод toBeziers от tinyspline используемый как раз над струбцинами NURBS автоматически, вам не нужно зажать его вручную.
Direct2D, более ясно ID2D1GeometrySink, не поддерживает сплайны, но кубические кривые Безье, которые могут быть объединены в сплайн. Напротив, вы можете получить b-кривые из ваших данных сплайна и просто добавить их в свою геометрию.
алгоритм просто объясняется этой картинкой: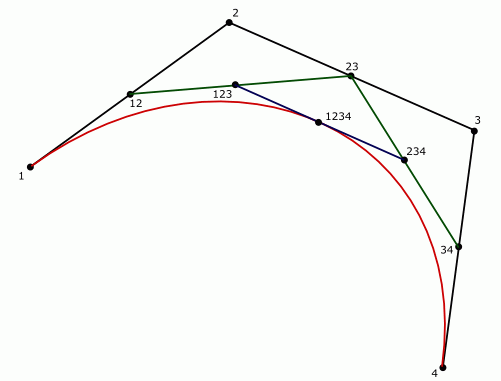 .
.
Статью для краткого и хорошо объяснения можно найти здесь. Вы можете разделить свой сплайн, пока контрольные точки не перекрываются, и степень может опускайтесь, даже до тех пор, пока все кривые не станут достаточно плоскими, чтобы быть линиями. Последнее-неплохая идея, потому что ваше оборудование не знает кривых, поэтому ваши пройденные кривые все равно преобразуются в линии. Когда вы сделайте это преобразование, вы можете определить допуск для плоскостности и избежать уродливых краев.
Я использовал этот пример кода для преобразования кардинального сплайна в список кубических патчей Безье: http://www.codeproject.com/Articles/31859/Draw-a-Smooth-Curve-through-a-Set-of-D-Points-wit
Он написан для WPF, но поскольку WPF и Direct2D отличаются только своей моделью программирования (декларативный и императивный), он очень легко переводится в Direct2D.
