Рисуя график корреляции в библиотек matplotlib

Предположим у меня есть набор данных дискретных векторов с n=2:

DATA = [
    ('a', 4),
    ('b', 5),
    ('c', 5),
    ('d', 4),
    ('e', 2),
    ('f', 5),
]

Как я могу построить этот набор данных с matplotlib, чтобы визуализировать любую корреляцию между двумя переменными?

любые простые примеры кода было бы здорово.

13
data-visualization graph matplotlib python

2 ответов

Джо Кингтон имеет правильный ответ, но ваш DATA вероятно, сложнее, что представлено. Он может иметь несколько значений "а". Способ Джо строит значения оси x быстро, но будет работать только для списка уникальных значений. Может быть, есть более быстрый способ сделать это, но вот как я это сделал:

import matplotlib.pyplot as plt

def assignIDs(list):
    '''Take a list of strings, and for each unique value assign a number.
    Returns a map for "unique-val"->id.
    '''
    sortedList = sorted(list)

    #taken from
    #http://stackoverflow.com/questions/480214/how-do-you-remove-duplicates-from-a-list-in-python-whilst-preserving-order/480227#480227
    seen = set()
    seen_add = seen.add
    uniqueList =  [ x for x in sortedList if x not in seen and not seen_add(x)]

    return  dict(zip(uniqueList,range(len(uniqueList))))

def plotData(inData,color):
    x,y = zip(*inData)

    xMap = assignIDs(x)
    xAsInts = [xMap[i] for i in x]


    plt.scatter(xAsInts,y,color=color)
    plt.xticks(xMap.values(),xMap.keys())


DATA = [
    ('a', 4),
    ('b', 5),
    ('c', 5),
    ('d', 4),
    ('e', 2),
    ('f', 5),
]


DATA2 = [
    ('a', 3),
    ('b', 4),
    ('c', 4),
    ('d', 3),
    ('e', 1),
    ('f', 4),
    ('a', 5),
    ('b', 7),
    ('c', 7),
    ('d', 6),
    ('e', 4),
    ('f', 7),
]

plotData(DATA,'blue')
plotData(DATA2,'red')

plt.gcf().savefig("correlation.png")

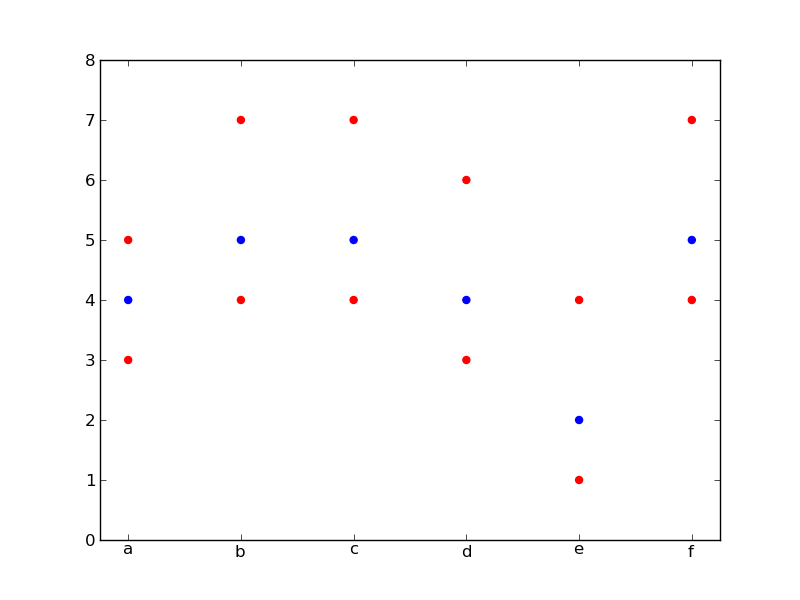
мой DATA2 set имеет два значения для каждого значения оси x. Он нарисован красным внизу.: enter image description here

редактировать

в вопрос вы задали очень широк. Я искал "корреляцию", и Википедия было хорошее обсуждение коэффициента момента продукта Пирсона, который характеризует наклон линейной подгонки. Имейте в виду, что это значение является только руководством и никоим образом не предсказывает, является ли линейная подгонка разумным предположением, см. Примечания на странице выше корреляция и нелинейность. Вот обновленный plotData метод, который использует numpy.linalg.lstsq сделать линейную регрессию и numpy.corrcoef чтобы вычислить R Пирсона:

import matplotlib.pyplot as plt
import numpy as np

def plotData(inData,color):
    x,y = zip(*inData)

    xMap = assignIDs(x)
    xAsInts = np.array([xMap[i] for i in x])

    pearR = np.corrcoef(xAsInts,y)[1,0]
    # least squares from:
    # http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.lstsq.html
    A = np.vstack([xAsInts,np.ones(len(xAsInts))]).T
    m,c = np.linalg.lstsq(A,np.array(y))[0]

    plt.scatter(xAsInts,y,label='Data '+color,color=color)
    plt.plot(xAsInts,xAsInts*m+c,color=color,
             label="Fit %6s, r = %6.2e"%(color,pearR))
    plt.xticks(xMap.values(),xMap.keys())
    plt.legend(loc=3)

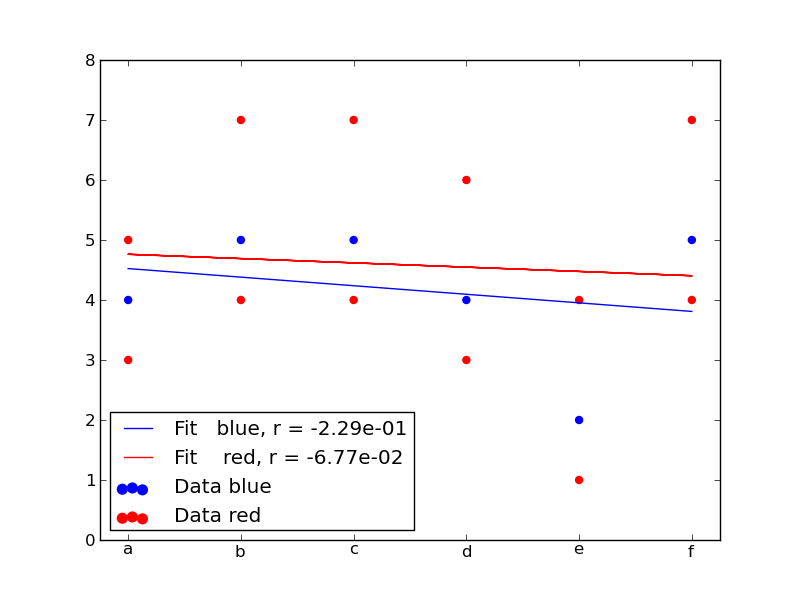
новая цифра: enter image description here

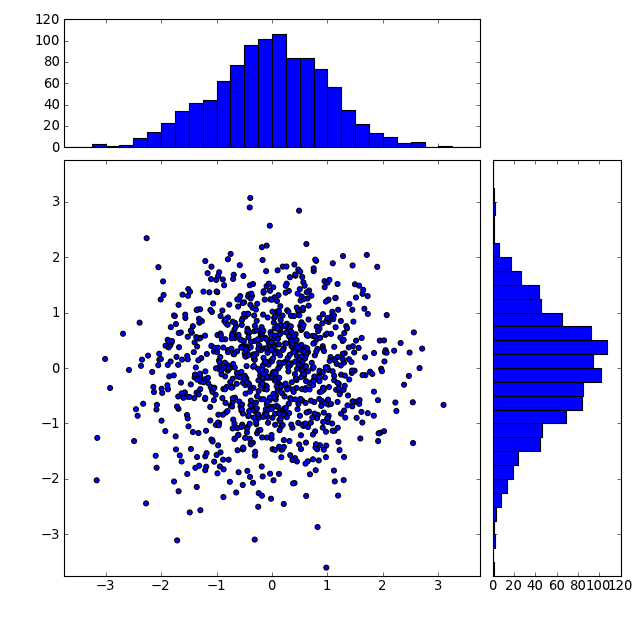
также сглаживание каждого направления и просмотр отдельных распределений могут быть полезны, и их примеры делать это в matplotlib: enter image description here

Если полезно линейное приближение, которое вы можете определить качественно, просто посмотрев на подгонку, вы можете вычесть этот тренд, прежде чем сглаживать направление y. Это поможет показать что у вас есть гауссовское случайное распределение о линейном тренде.

19

Я немного запутался... Есть несколько способов сделать что-то в этом направлении. Первые два, которые приходят на ум, - это простой участок ствола или участок рассеяния.

вы просто хотите построить сюжет, используя сюжет stem, как это?

import matplotlib.pyplot as plt
data = [
    ('a', 4),
    ('b', 5),
    ('c', 5),
    ('d', 4),
    ('e', 2),
    ('f', 5),
]
labels, y = zip(*data)

x = range(len(y))
plt.stem(x, y)
plt.xticks(x, labels)
plt.axis([-1, 6, 0, 6])
plt.show()

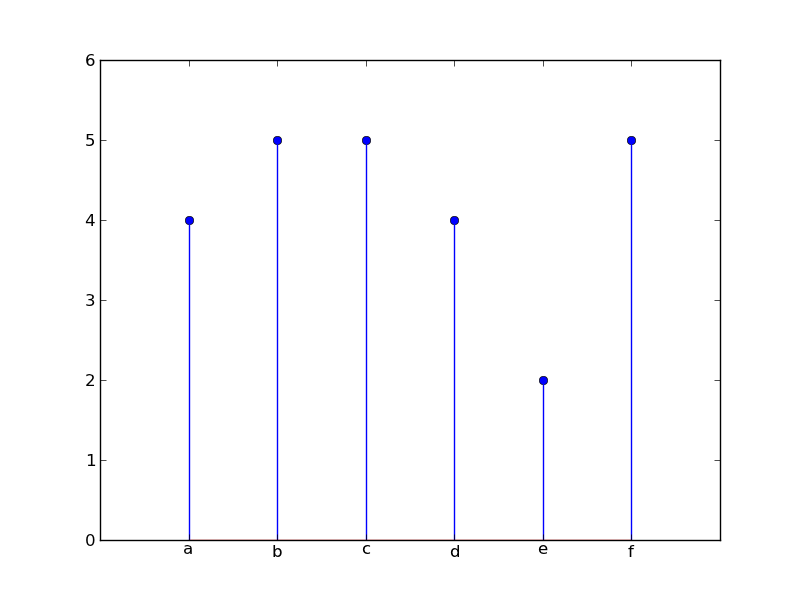
enter image description here

или разброс, как это:

import matplotlib.pyplot as plt
data = [
    ('a', 4),
    ('b', 5),
    ('c', 5),
    ('d', 4),
    ('e', 2),
    ('f', 5),
]
labels, y = zip(*data)

x = range(len(y))
plt.plot(x, y, 'o')
plt.xticks(x, labels)
plt.axis([-1, 6, 0, 6])
plt.show()

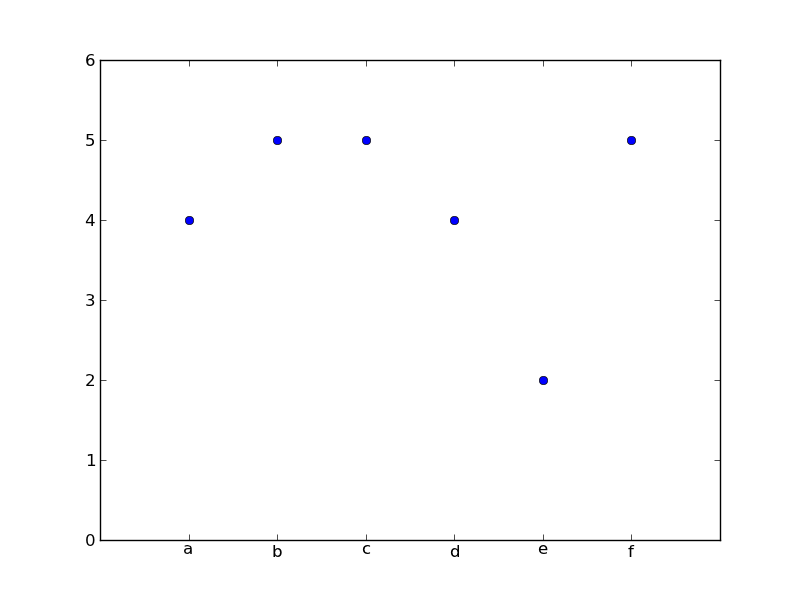
enter image description here

или что-то еще?

6