Самая длинная цепочка элементов из списка в Python
у меня есть список наций, и я хочу иметь самый длинный путь наций, где каждая выбранная страна должна начинаться с той же буквы, которая закончилась предыдущим элементом
nations = ['albania','andorra','austria','belarus','belgium','bosnia and herzegovina',
'bulgaria','croatia','czech republic','denmark','estonia',
'finland','france','germany','greece','hungary',
'iceland','ireland','italy','latvia','liechtenstein','lithuania','luxembourg',
'macedonia','malta','moldova','monaco','montenegro','netherlands',
'norway','poland','portugal','romania','russia',
'san marino','serbia','slovakia','slovenia','spain','sweden', 'switzerland',
'ukraine','united kingdom','vatican city']
chain('spain')
>>>['spain', 'netherlands', 'slovenia', 'andorra', 'austria', 'albania']
Я пробовал этот способ, но он не работает
def chain(naz):
initial = naz[-1]
initials=[]
res = set()
res.add(naz)
for i in nations:
if i.startswith(initial):
initials.append(i)
for j in initials:
nations.remove(j)
res.add(j)
chain(j)
return res
любое предложение?
4 ответов
Я также пошел на рекурсивный спуск. Не уверен, что динамическое программирование хорошо подходит для этого, поскольку список изменяется по мере продвижения. Немного компактнее и не нужно начинать удаляться из списка перед вызовом цепочки. :-)
def chain(start, countries):
remaining = list(countries)
del remaining[remaining.index(start)]
possibles = [x for x in remaining if x[:1] == start[-1:]]
maxchain = []
for c in possibles:
l = chain(c, remaining)
if len(l) > len(maxchain):
maxchain = l
return [start] + maxchain
звонок такой. :-)
>>> chain('spain', nations)
['spain', 'netherlands', 'serbia', 'albania', 'andorra', 'austria']
вот некоторые комментарии:
- вы хотите вернуть путь. Так это упорядоченная коллекция, не так ли? Вероятно, вы не должны использовать набор для res, так как набор неупорядочен
- вы знаете длину la или возвращенный путь? Нет, не знаешь. Так что вам может понадобиться
whileгде-то -
i.startswith(initial)истинно, только если я начинаю со всего начального слова. Вы, вероятно, не хотите этого - вы пытаетесь использовать подход recurcive. Однако вы не собираете результат. В recurcive звонить бесполезно на данный момент
-
nationsявляется глобальной переменной, что плохо
редактировать
ошибки, описанные в вашем комментарии может произойти потому, что ваш recurcive звонок внутри J в цикле. В recurcive звонок может удалить элементы для народов, которые также могут существовать в инициалы. Таким образом, вы пытаетесь удалить их более одного раза, что вызывает исключение. Вы, вероятно, хотите поставить chain(j) вне цикла (и, возможно, использовать его возвращаемое значение?)
в качестве примечания, ваша проблема NP-полная (это означает, что у нее нет "быстрого" полиномиального решения.) Это решаемо для небольших размеров проблемы, но это становится очень трудно очень быстро.
ваша проблема может рассматриваться как проблема с самым длинным путем на направленном графике.
- рисовать ориентированный граф С каждым словом (страной), представленным в виде вершины.
- за каждую пару слов,
w1иw2, провести edgew1 -> w2если последняя букваw1Это то же самое, что и первая букваw2. - также нарисуйте обратный край от
w2->w1еслиw2последняя буква s такая же, какw1s первая буква. - найти максимальная длина пути - простой путь, содержащий наибольшее количество вершин. ("простой "в этом случае означает" не включать любую вершину более одного раза.")
вот пример графика для списка фруктов и овощей: Apple, banana, eggplant, kiwifruit, orange, oregano, tangerine, zucchini.
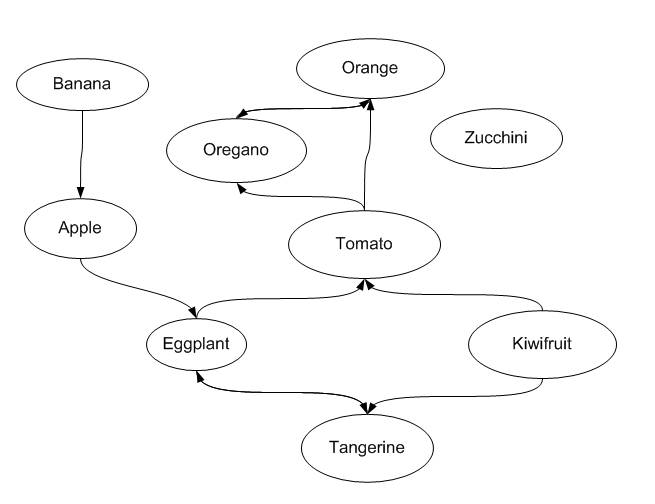
этот график может содержать циклы (например, этот график имеет цикл eggplant -> tangerine -> eggplant -> tangerine..... самая длинная задача пути для направленных графов, содержащих циклы, является NP-полной. поэтому для этой задачи нет полиномиального решения.
это не значит, что вы не можете сделать лучше, чем грубая сила. существует алгоритм динамического программирования это уменьшает сложность от O(n!) (факториал, очень БАД) к O(n^2 * 2^n) (superexponential, все равно плохо, но лучше, чем факториал.)
это наивный рекурсивный подход... я чувствую, что вы могли бы использовать динамическое программирование и было бы лучше
def chain(start,options):
#start is the starting word
#options are the words left
next_options = [country for country in options if country[0] == start[-1]]
#if theres no options, return the single
if not next_options:
return [start]
#otherwise, return best chain out of the next option
best_chain = None
longest_chain = 0
for option in next_options:
new_options = options[:]
new_options.remove(option)
possible_chain = chain(option,new_options)
if len(possible_chain) > longest_chain:
best_chain = possible_chain
longest_chain = len(possible_chain)
return [start] + best_chain
