shapely и matplotlib точка-в-полигоне не точны с геолокацией

Я тестирую функцию point-in-polygon с matplotlib и shapely.

здесь карта содержит многоугольник Бермудского треугольника.

Google maps's point-in-polygon функции ясно показывает testingPoint и testingPoint2 находятся внутри полигона, который является правильным результатом.

Если я проверю две точки в библиотек matplotlib и shapely, только point2 проходит тест.

In [1]: from matplotlib.path import Path

In [2]: p = Path([[25.774252, -80.190262], [18.466465, -66.118292], [32.321384, -64.75737]]) 

In [3]: p1=[27.254629577800088, -76.728515625]

In [4]: p2=[27.254629577800088, -74.928515625]

In [5]: p.contains_point(p1)
Out[5]: 0

In [6]: p.contains_point(p2)
Out[6]: 1

фигуристая показывает тот же результат, что и matplotlib.

In [1]: from shapely.geometry import Polygon, Point

In [2]: poly = Polygon(([25.774252, -80.190262], [18.466465, -66.118292], [32.321384, -64.75737]))

In [3]: p1=Point(27.254629577800088, -76.728515625)

In [4]: p2=Point(27.254629577800088, -74.928515625)

In [5]: poly.contains(p1)
Out[5]: False

In [6]: poly.contains(p2)
Out[6]: True

что на самом деле происходит? Это алгоритм Google лучше, чем эти два?

спасибо

8
google-maps-api-3 matplotlib point-in-polygon python shapely

4 ответов

помните: мир не плоский! Если проекция Google Maps-это ответ, который вы хотите, вам нужно проецировать географические координаты на сферический Меркатор чтобы получить другой набор координат X и y. Pyproj может помочь с этим, просто убедитесь, что вы изменили свои координатные оси перед (т. е.: X, Y или долгота, широта).

import pyproj
from shapely.geometry import Polygon, Point
from shapely.ops import transform
from functools import partial

project = partial(
    pyproj.transform,
    pyproj.Proj(init='epsg:4326'),
    pyproj.Proj('+proj=merc +a=6378137 +b=6378137 +lat_ts=0.0 +lon_0=0.0 +x_0=0.0 +y_0=0 +k=1.0 +units=m +nadgrids=@null +no_defs'))

poly = Polygon(([-80.190262, 25.774252], [-66.118292, 18.466465], [-64.75737, 32.321384]))
p1 = Point(-76.728515625, 27.254629577800088)

# Old answer, using long/lat coordinates
poly.contains(p1)  # False
poly.distance(p1)  # 0.01085626429747994 degrees

# Translate to spherical Mercator or Google projection
poly_g = transform(project, poly)
p1_g = transform(project, p1)

poly_g.contains(p1_g)  # True
poly_g.distance(p1_g)  # 0.0 meters

Кажется, получает правильный ответ.

9

хотя вы уже приняли ответ, но в дополнение к ответу @MikeT я добавлю это для будущих посетителей, которые могут захотеть сделать то же самое с matplotlib и базовая карта на mpl_toolkit :

from mpl_toolkits.basemap import Basemap
from matplotlib.path import Path


# Mercator Projection
# http://matplotlib.org/basemap/users/merc.html
m = Basemap(projection='merc', llcrnrlat=-80, urcrnrlat=80,
            llcrnrlon=-180, urcrnrlon=180, lat_ts=20, resolution='c')

# Poly vertices
p = [[25.774252, -80.190262], [18.466465, -66.118292], [32.321384, -64.75737]]

# Projected vertices
p_projected = [m(x[1], x[0]) for x in p]

# Create the Path
p_path = Path(p_projected)

# Test points
p1 = [27.254629577800088, -76.728515625]
p2 = [27.254629577800088, -74.928515625]

# Test point projection
p1_projected = m(p1[1], p1[0])
p2_projected = m(p2[1], p2[0])

if __name__ == '__main__':
    print(p_path.contains_point(p1_projected))  # Prints 1
    print(p_path.contains_point(p2_projected))  # Prints 1
9

Я просто сделал это, чтобы проверить, если точки находятся внутри треугольника:

from matplotlib import pylab as plt
poly = [[25.774252, -80.190262],
        [18.466465, -66.118292],
        [32.321384, -64.75737],
        [25.774252, -80.190262]]
x = [point[0] for point in poly]
y = [point[1] for point in poly]
p1 = [27.254629577800088, -76.728515625]
p2 = [27.254629577800088, -74.928515625]
plt.plot(x,y,p1[0],p1[1],'*r',p2[0],p2[1],'*b')
plt.show()

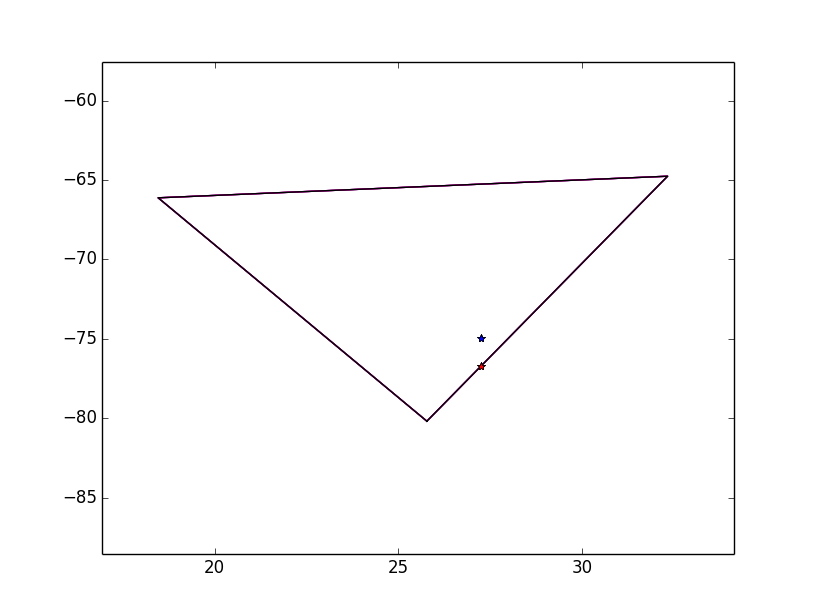
Image shows point 1 is not inside the triangle

теперь, когда вы используете Google Maps и многоугольник отображается на сферические координаты, треугольник деформируется, что следует иметь в виду.

в любом случае, построение ваших данных с помощью kml в Gookle Earth также показывает точку вне треугольника?!

<kml>
<Document>
<Placemark><name>Point 1</name><Point>
<coordinates> -76.728515625, 27.254629577800088,0</coordinates></Point></Placemark>
<Placemark><name>Point 2</name><Point>
<coordinates>-74.928515625, 27.254629577800088,     0</coordinates></Point></Placemark>
<Placemark><name>Poly</name><Polygon>
<outerBoundaryIs><LinearRing>
<coordinates> -80.190262,25.774252 -66.118292,18.466465 -64.75737,32.321384 -80.190262,25.774252</coordinates>
</LinearRing></outerBoundaryIs>
</Polygon></Placemark>
</Document>
</kml>

такое же возникновение как в изображении matplotlib, пункт 1 slighlty вне треугольник, при построении в евклидовых 2D-координатах. Для геометрических вычислений в гео-координатах проверьте QGIS Python Console или GDAL / OGR Tools. Или вы могли бы использовать Google maps api, как и в Примере, который связан с на этой странице, где тема 2D-геометрии против геодезической геометрии является coverd.

2

чтобы проверить, содержит ли многоугольник несколько точек, я бы использовал matplotlib contains_points, задокументировано здесь:http://matplotlib.org/api/path_api.html#matplotlib.path.Path.contains_points

это делает один большой вызов с использованием массива numpy, поэтому он эффективен. Обратите внимание, что вы можете передать радиус, который фактически раздувает или удаляет многоугольник ,вы также можете преобразовать (проекции...) перед выполнением проверки.

0