Шестиугольные сетки, как вы находите, в каком шестиугольнике находится точка?
У меня есть карта, состоящая из строк и столбцов шестиугольников
Это не фактическое изображение шестнадцатеричной карты, которую я использую, но использует шестиугольники того же размера и формы
Я должен быть в состоянии сказать, какой из них мыши над, когда пользователь нажимает,
каждый шестиугольник представлен экземпляром класса "плитка", однако это не содержит каких-либо данных о местоположении или даже полигона, поэтому в основном единственный способ узнать, где находится конкретный шестиугольник, это знать его положение в 2D массива.
я использовал квадратную сетку раньше, и было относительно легко выяснить, какой квадрат был выбран, потому что пиксели также квадратные,
// example where each square is 10 by 10 pixels:
private void getClickedSquare(MouseEvent me)
{
int mouseX = me.getX();// e.g. 25
int mouseY = me.getY();// e.g. 70
int squareX= (int) (mouseX / 10);// in this case 2
int squareY= (int) (mouseY / 10);// in this case 7
//then to access the tile I would do
map.squares[squareX][squareY].whatever();
}
но я даже не уверен, с чего начать с шестиугольников, есть ли у кого-нибудь опыт?
Я не могу использовать полигоны (Java), так как, когда я перемещаю карту по экрану и увеличиваю ее размер, я столкнусь с проблемами с обновлением огромного количества полигонов каждый рамка. Хотя тогда я мог бы просто проверить, включена ли точка в любой из полигонов плитки карты!
на данный момент отображается шестигранники лишь BufferedImages.
Если вы хотите знать больше информации, пожалуйста, спросите, Спасибо за ваше время :D
6 ответов
(обновлено: рефакторинг кода, чтобы сделать более понятным и более эффективным) (Обновлено: уменьшена длина ответа, исправлены ошибки в коде, улучшено качество изображений)
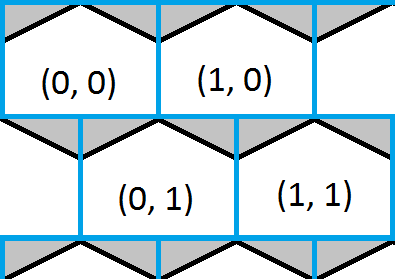
Это изображение показывает верхний левый угол шестиугольной сетки и накладывается синяя квадратная сетка. Легко найти, какой из квадратов точка находится внутри, и это даст грубое приближение того, какой шестиугольник тоже. Белые части шестиугольников показывают, где квадратная и шестиугольная сетка разделяют те же координаты и серые части шестиугольников показывают, где они не делают.
решение теперь так же просто, как найти, в каком поле находится точка, а затем проверить, находится ли точка в любом из треугольников, и при необходимости исправить ответ.
private final Hexagon getSelectedHexagon(int x, int y)
{
// Find the row and column of the box that the point falls in.
int row = (int) (y / gridHeight);
int column;
boolean rowIsOdd = row % 2 == 1;
// Is the row an odd number?
if (rowIsOdd)// Yes: Offset x to match the indent of the row
column = (int) ((x - halfWidth) / gridWidth);
else// No: Calculate normally
column = (int) (x / gridWidth);
в этот момент у нас есть строка и столбец окна, в котором находится наша точка, затем нам нужно проверить нашу точку против двух верхних краев шестиугольника, чтобы увидеть, лежит ли наша точка в любом из шестиугольников сверху:
// Work out the position of the point relative to the box it is in
double relY = y - (row * gridHeight);
double relX;
if (rowIsOdd)
relX = (x - (column * gridWidth)) - halfWidth;
else
relX = x - (column * gridWidth);
наличие относительных координат облегчает следующий шаг.
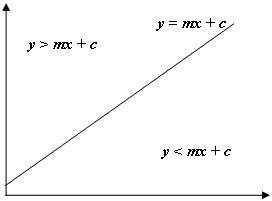
как на изображении выше, если y нашей точки > mx + c мы знаем, что наша точка лежит выше линии, а в нашем случае шестиугольник выше и слева от текущей строки и столбца. обратите внимание, что система координат в java имеет y, начиная с 0 в левом верхнем углу экрана, а не в левом нижнем углу, как обычно в математика, следовательно, отрицательный градиент, используемый для левого края,и положительный градиент, используемый для правого.
// Work out if the point is above either of the hexagon's top edges
if (relY < (-m * relX) + c) // LEFT edge
{
row--;
if (!rowIsOdd)
column--;
}
else if (relY < (m * relX) - c) // RIGHT edge
{
row--;
if (rowIsOdd)
column++;
}
return hexagons[column][row];
}
краткое описание переменных, используемых в приведенном выше примере:
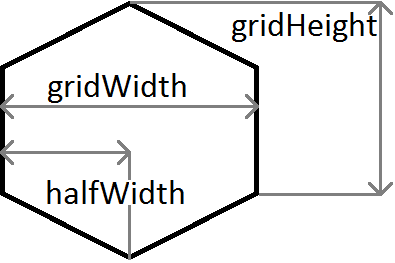
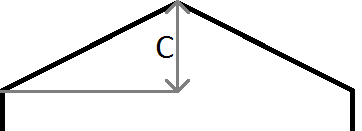
м-градиент, так m = c / halfWidth
EDIT: этот вопрос сложнее, чем я думал сначала, я перепишу свой ответ с некоторой работой, однако я не уверен, является ли путь решения улучшением других ответов.
вопрос можно перефразировать: при любом x, y найти шестиугольник, центр которого ближе всего к x, y
т. е. минимизировать dist_squared (Hex[n].центр, (x, y)) над n (квадрат означает, что вам не нужно беспокоиться о квадратных корнях, которые экономят некоторый процессор)
, сначала мы должны сузить количество шестиугольников для проверки - мы можем сузить его до максимума 5 следующим способом: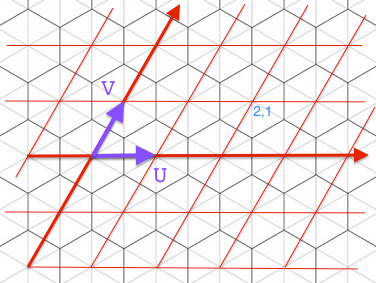
Итак, первый шаг-выразить свою точку (x, y) в УФ-пространстве т. е. (x, y) = лямбдаU + muV, so = (лямбда, mu) в УФ-пространстве
Это просто 2D-матричное преобразование (http://playtechs.blogspot.co.uk/2007/04/hex-grids.html может быть полезно, если вы не понимаете линейный трансформация.)
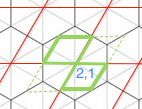
теперь, учитывая точку (лямбда, mu), если мы округляем оба до ближайшего целого числа, то у нас есть это:
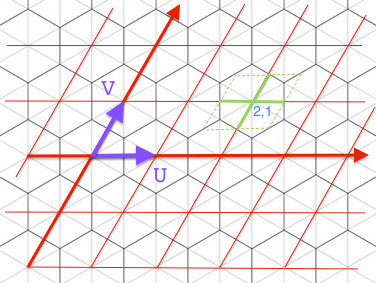
везде в пределах зеленых квадратных карт обратно в (2,1)
таким образом, большинство точек в этом зеленом квадрате будут правильными, т. е. они находятся в шестиугольнике (2,1).
но некоторые точки должны возвращать шестиугольник # (2,2), i.e:
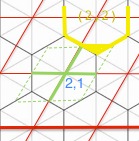
аналогично некоторые должны возвращать шестиугольник # (3,1). И тогда на противоположном углу этого зеленого параллелограмма будет еще 2 области.
Итак, чтобы суммировать, если int (lambda,mu) = (p,q), то мы,вероятно, внутри шестиугольника (p,q), но мы также можем быть внутри шестиугольников (p+1,q), (p, q+1), (p-1, q) или (p, q-1)
несколько способов определить, какой из них имеет место. Проще всего было бы преобразовать центры всех этих 5 шестиугольников обратно в исходную систему координат и найти наиболее близкую к нашей точка.
но оказывается, вы можете сузить это до ~50% времени, не делая никаких проверок расстояния, ~25% времени, делая одну проверку расстояния, а остальные ~25% времени, делая 2 проверки расстояния (я предполагаю, что цифры, глядя На области, каждая проверка работает на):
p,q = int(lambda,mu)
if lambda * mu < 0.0:
// opposite signs, so we are guaranteed to be inside hexagon (p,q)
// look at the picture to understand why; we will be in the green regions
outPQ = p,q
else:
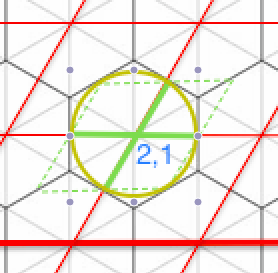
// circle check
distSquared = dist2( Hex2Rect(p,q), Hex2Rect(lambda, mu) )
if distSquared < .5^2:
// inside circle, so guaranteed inside hexagon (p,q)
outPQ = p,q
else:
if lambda > 0.0:
candHex = (lambda>mu) ? (p+1,q): (p,q+1)
else:
candHex = (lambda<mu) ? (p-1,q) : (p,q-1)
и этот последний тест можно убрать:
else:
// same sign, but which end of the parallelogram are we?
sign = (lambda<0) ? -1 : +1
candHex = ( abs(lambda) > abs(mu) ) ? (p+sign,q) : (p,q+sign)
теперь мы сузили его до одного другие возможный шестиугольник, нам просто нужно найти, который ближе:
dist2_cand = dist2( Hex2Rect(lambda, mu), Hex2Rect(candHex) )
outPQ = ( distSquared < dist2_cand ) ? (p,q) : candHex
функция Dist2_hexSpace(A,B) будет убирать вещи дальше.
Это дополнение к ответу Себастьянтроя. Я бы оставил это как комментарий, но у меня пока недостаточно репутации.
Если вы хотите реализовать осевую систему координат, как описано здесь: http://www.redblobgames.com/grids/hexagons/
Вы можете внести небольшие изменения в код.
вместо
// Is the row an odd number?
if (rowIsOdd)// Yes: Offset x to match the indent of the row
column = (int) ((x - halfWidth) / gridWidth);
else// No: Calculate normally
column = (int) (x / gridWidth);
использовать
float columnOffset = row * halfWidth;
column = (int)(x + columnOffset)/gridWidth; //switch + to - to align the grid the other way
это сделает координату (0, 2) на том же диагональном столбце, что и (0, 0) и (0, 1) вместо того, чтобы непосредственно ниже (0, 0).
Я начал с того, что посмотрел на ответ @pi https://stackoverflow.com/a/23370350/5776618 и подумал, что было бы интересно попробовать что-то подобное в координатах куба с UVW-пространством (а не 2D, осевым, UV-пространством).
следующие уравнения map (x,y) = > (u,v,w)
u = (2/3)*x;
v = -(1/3)*x + (1/2)*y;
w = -(1/3)*x - (1/2)*y;
тогда это так же просто, как округления u, v и w до ближайшего целого числа и преобразования обратно в x, y. Однако это большая загвоздка...
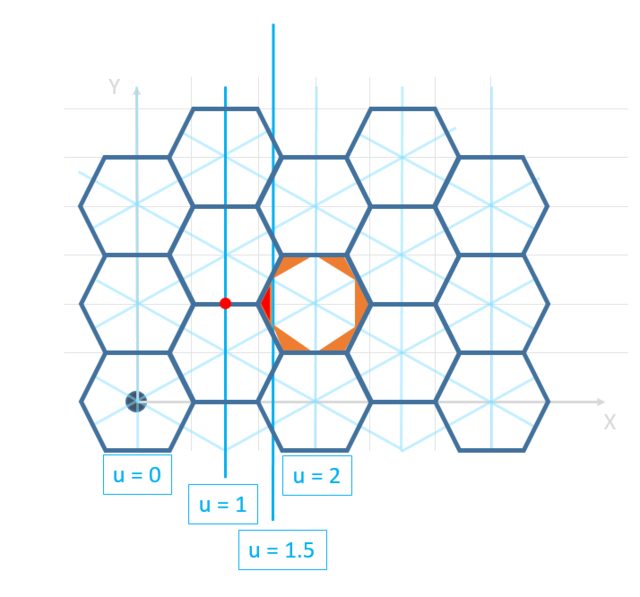
в ответе выше отмечается, что округление в УФ-пространстве будет иметь несколько областей, которые отображаются неправильно:
Это все еще происходит при использовании координат Куба:
Любая область в оранжевых треугольниках составляет > 0,5 единицы от центра шестиугольника и при округлении будет округляться от центра. Это показано выше, как что-либо в красном треугольнике (слева от линии u=1.5) будет иметь U, округленный неправильно до u=1, а не u=2.
некоторые ключевые наблюдения здесь...
1. Оранжевые / красные проблемные области не перекрываются
2. В координатах Куба действительные шестнадцатеричные центры имеют u + v + w = 0
в приведенном ниже коде u, v и w округляются с самого начала как округление только в проблеме, если округленные координаты не суммируются до нуля.
uR = Math.round(u);
vR = Math.round(v);
wR = Math.round(w);
если они не суммируются до нуля, поскольку проблемные области не перекрываются, будет только 1 координата, которая округляется неправильно. Эта координата также является координатой, которая была округлена больше всего.
arr = [ Math.abs(u-uR), Math.abs(v-vR), Math.abs(w-wR) ];
var i = arr.indexOf(Math.max(...arr));
после того, как координата задачи найдена, она округляется в другом направлении. Окончательный (x,y) затем вычисляется из округленного/скорректированного (u,v, w).
nearestHex = function(x,y){
u = (2/3)*x;
v = -(1/3)*x + (1/2)*y;
w = -(1/3)*x - (1/2)*y;
uR = Math.round(u);
vR = Math.round(v);
wR = Math.round(w);
if(uR+vR+wR !== 0){
arr = [ Math.abs(u-uR), Math.abs(v-vR), Math.abs(w-wR) ];
var i = arr.indexOf(Math.max(...arr));
switch(i){
case 0:
Math.round(u)===Math.floor(u) ? u = Math.ceil(u) : u = Math.floor(u);
v = vR; w = wR;
break;
case 1:
Math.round(v)===Math.floor(v) ? v = Math.ceil(v) : v = Math.floor(v);
u = uR; w = wR;
break;
case 2:
Math.round(w)===Math.floor(w) ? w = Math.ceil(w) : w = Math.floor(w);
u = uR; v = vR;
break;
}
}
return {x: (3/2)*u, y: v-w};
}
Я еще раз посмотрел на http://playtechs.blogspot.co.uk/2007/04/hex-grids.html и это очень аккуратно математически.
однако подход Себастьяна, похоже, режет погоню и выполняет задачу в удивительно немногих строках кода.
Если вы прочитали раздел комментариев, Вы можете найти, что кто-то написал реализацию Python вhttp://gist.github.com/583180
Я перепробую это здесь для потомство:
# copyright 2010 Eric Gradman
# free to use for any purpose, with or without attribution
# from an algorithm by James McNeill at
# http://playtechs.blogspot.com/2007/04/hex-grids.html
# the center of hex (0,0) is located at cartesian coordinates (0,0)
import numpy as np
# R ~ center of hex to edge
# S ~ edge length, also center to vertex
# T ~ "height of triangle"
real_R = 75. # in my application, a hex is 2*75 pixels wide
R = 2.
S = 2.*R/np.sqrt(3.)
T = S/2.
SCALE = real_R/R
# XM*X = I
# XM = Xinv
X = np.array([
[ 0, R],
[-S, S/2.]
])
XM = np.array([
[1./(2.*R), -1./S],
[1./R, 0. ]
])
# YM*Y = I
# YM = Yinv
Y = np.array([
[R, -R],
[S/2., S/2.]
])
YM = np.array([
[ 1./(2.*R), 1./S],
[-1./(2.*R), 1./S],
])
def cartesian2hex(cp):
"""convert cartesian point cp to hex coord hp"""
cp = np.multiply(cp, 1./SCALE)
Mi = np.floor(np.dot(XM, cp))
xi, yi = Mi
i = np.floor((xi+yi+2.)/3.)
Mj = np.floor(np.dot(YM, cp))
xj, yj = Mj
j = np.floor((xj+yj+2.)/3.)
hp = i,j
return hp
def hex2cartesian(hp):
"""convert hex center coordinate hp to cartesian centerpoint cp"""
i,j = hp
cp = np.array([
i*(2*R) + j*R,
j*(S+T)
])
cp = np.multiply(cp, SCALE)
return cp
Я не знаю, поможет ли это кому-нибудь, но я придумал гораздо более простое решение. Когда я создаю свой шестиугольник, я просто даю им среднюю точку и, найдя ближайшую среднюю точку с помощью мыши coordonate, я могу найти, на котором один im!