Сложение и умножение в поле Галуа
Я пытаюсь генерировать QR-коды на чрезвычайно ограниченной встроенной платформе. Все в спецификация Кажется довольно простым, за исключением для генерации кодовых слов коррекции ошибок. Я посмотрел на кучу существующих реализаций, и все они пытаются реализовать кучу полиномиальной математики, которая идет прямо над моей головой, особенно касаемо полей Галуа. Самый простой способ, который я могу видеть, как в математической сложности, так и в требования к памяти-это концепция схемы, которая изложена в самой спецификации:
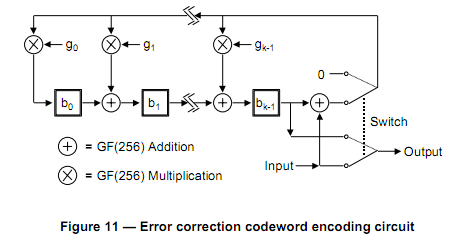
с их описанием я довольно уверен, что смогу реализовать это, за исключением частей с надписью GF(256) addition и GF(256) Multiplication.
Они предлагают эту помощь:
полиномиальная арифметика для QR-кода рассчитывается с использованием битовой арифметики по модулю 2 и байтовой арифметики по модулю 100011101 арифметика. Это Галуа. поле 2^8 с 100011101, представляющим основной модуль поля полином x^8+x^4+x^3+x^2+1.
что для меня почти все греческое.
Итак, мой вопрос таков: каков самый простой способ выполнить сложение и умножение в этом виде арифметики поля Галуа? Предположим, что оба входных номера имеют ширину 8 бит, а мой выход также должен быть 8 бит. Несколько реализаций предварительно вычисляют или hardcode в двух таблицах поиска, чтобы помочь с этим, но я не уверен, как они рассчитаны, или как я буду использовать их в этой ситуации. Я бы предпочел не брать 512-байтовую память для двух таблиц, но это действительно зависит от того, какая альтернатива. Мне просто нужна помощь в понимании того, как выполнить одну операцию умножения и сложения в этой схеме.
2 ответов
на практике требуется только одна таблица. Это было бы для умножения GP(256). Обратите внимание, что вся арифметика без переноса, что означает, что нет распространения переноса.
сложение и вычитание без переноса эквивалентно xor.
так в GF(256), a + b и a - b оба эквивалентно a xor b.
умножение GF(256) также носит-менее, и может быть сделано используя снесите-менее умножение в подобном путе с снесите-менее сложение/вычитание. Это можно сделать эффективно с помощью аппаратной поддержки через say набор инструкций Intel CLMUL.
однако, трудная часть, уменьшает модуль 100011101. В обычном целочисленном делении вы делаете это, используя ряд шагов сравнения/вычитания. В GF (256) вы делаете это почти идентичным образом, используя серию шагов сравнения/xor.
на самом деле, это достаточно плохо, где все еще быстрее просто предварительно вычислить все 256 x 256 умножает и положить их в таблицу поиска 65536-entry.
Страница 3 следующего pdf имеет довольно хорошую ссылку на арифметику GF256:
http://www.eecs.harvard.edu / ~michaelm / CS222 / eccnotes.pdf
Я сделал реализацию исправления ошибок Рида-Соломона с помощью GF (256), но это было с полиномом 10010010 вместо 100011101.
(Я следую указателю на zxing в первом ответе, так как я автор.)
ответ о сложении совершенно правильный, поэтому работать в этой области удобно на компьютере.
да умножение работает, и для GF256. * Б-то же, как EXP(log(а) + лог(б)). И потому что GF256 имеет только 256 элементов, есть только 255 уникальных полномочий "x", и то же самое для журнала. Таким образом, их легко поместить в таблицу поиска. Таблицы "обернутся" на 256, поэтому вы увидите "% size". "/size " немного сложнее объяснить в предложении - это потому, что на самом деле 1-255 "wrap around", а не 0-255. Так что нужен не просто модуль.
заключительная часть, возможно, заключается в том, как вы уменьшаете по модулю неприводимый многочлен. Неприводимый многочлен равен x^8 plus некоторые члены более низкой мощности, правильно-назовите его I(x) = x^8 + R (x). И многочлен конгруэнтен 0 в поле по определению; I (x) == 0. Итак, x^8 = = - R (x). И, удобно, сложение и вычитание одинаковы, поэтому x^8 == -R(x) == R(x).
единственный раз, когда нам нужно уменьшить многочлены более высокой мощности, - это при построении таблицы экспонент. Вы просто продолжаете умножать на x (это сдвиг влево), пока он не станет слишком большим-получает член x^8. Но x^8 совпадает с R(x). Так что вы берете x^8 и добавить в R (x). R(x) просто имеет полномочия до x^7, поэтому все это еще в байте, все в GF (256). И вы знаете, как добавить в это поле.
помогает?
