Сложность алгоритма в онлайн-тесте

я должен был пройти онлайн-тест программирования для стажировки и получил вопрос по анализу сложности. Я ответил на вопрос и он был обозначен неправильно, и я просто хотел бы понять, почему, чтобы я мог улучшить.

Вопрос:

дайте сложность для следующего алгоритма, когда reverseOrder истинен и когда он ложен:

List<int> stackToList(Stack<int> stack, bool reverseOrder) {
    List<int> items = new List<int>();

    while (stack.Count > 0) {
        int item = stack.Pop();

        if (reverseOrder) {
            items.Insert(0, item);
        } else {
            items.Add(item);
        }
    }

    return items;
}

EDIT: он был множественный выбор, и возможные ответы были:

  • O (1)
  • O (nlogn)
  • O (n)
  • O (n^2)

вы можете выбрать один для того, когда reverseOrder истинен, а другой для того, когда он ложен.

Мой Ответ:

  • когда reverseOrder true: O (n2)
  • когда reverseOrder false: O (n2)

я получил этот ответ следующим образом:

  • цикл while будет повторяться n раз, потому что он продолжается, пока не останется элемента, чтобы выскочить
  • Pop() и O(1)

  • в случае reverseOrder будучи true, an Insert в начале списка сделано. С List<T> поддерживается массивом, он динамически изменяется и каждый элемент перемещается вверх по одному пробелу, и элемент вставляется в индекс 0. Согласно https://msdn.microsoft.com/en-us/library/sey5k5z4 (v=против 110).aspx:

    этот метод является операцией O(n), где n-количество.

  • в случае reverseOrder будучи false, an Add для добавления элемента в конец списка. С items не задан начальный размер,Count не менее Capacity, что приводит к изменению размера, Итак, согласно https://msdn.microsoft.com/en-us/library/3wcytfd1 (v=против 110).aspx:

    если Count меньше емкости, этот метод является операцией O(1). Если емкость должна быть увеличена для размещения нового элемента, этот метод становится операцией O(n), где N-Count.

я чувствую себя довольно обескураженным в данный момент, так как получение этого неправильно вызвало мой счет, чтобы упасть, хотя я получил все другие вопросы по тесту правильные.

7
asymptotic-complexity c#

4 ответов

вам нужно спросить людей, которые написали тест. Любой ответ здесь будет строго основан на мнении, так как у нас нет полного контекста, т. е. что привело бы автора теста к описанию сложности алгоритма иначе, чем у вас.

тем не менее, я бы согласился с автором теста на reverseOrder == false сценарий. Хотя это правда, что вы мая выполните операцию изменения размера во время вызова Add(), операция изменения размера будет вводить в худшем случае log N стоимость, так как новый размер удваивается с каждым изменением размера.

вы не говорите, Каким должен быть правильный ответ, но я бы дал его как O(N log N).

4

ваше предположение, что емкость увеличивается каждый раз, когда вы добавляете элемент - это не правильно. В документации, похоже, не упоминается точный алгоритм, но я считаю, что он удваивается каждый раз, когда емкость увеличивается. Вы можете видеть, что в образце о динозаврах в документации, которую вы связали-они добавляют 5 динозавров и отчеты о емкости как 8.

1

глядя на строку 6669

http://referencesource.microsoft.com/#mscorlib/system/collections/generic/list.cs,cf7f4095e4de7646

ясно, что вставка в начале списка заставляет копии полностью вниз по списку. Поэтому для каждой вставки требуется N ходов. O (N^2) Мне кажется.

0

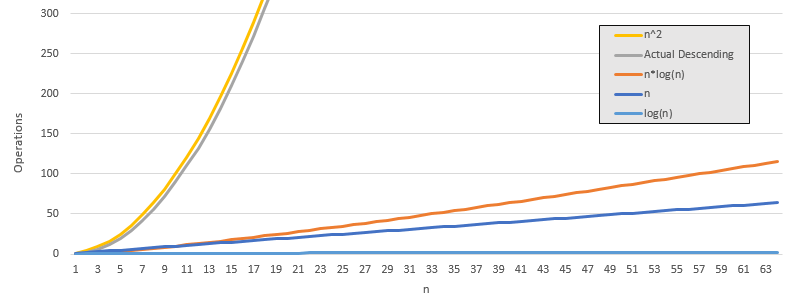
stackToList (stack, true)= O (n). В большинстве случаев этот вызов будет O (1). Однако, когда список.Функция Add должна расширять больше своей емкости, массив должен быть скопирован в новый массив с емкостью в два раза больше предыдущей и повторять предыдущие элементы, чтобы сохранить их в новом массиве. Таким образом, мы можем представить фактическую операцию в excel, как если бы(nLOG (n,2)(n/2)/INT (nLOG (n,2)(n/2)) = 1, n, 1). Учитывая, что нет узкие места ресурсов, если этот алгоритм завершен за 10 секунд с 10 миллионами элементов, чтобы завершить 100 миллионов элементов, вы ожидаете, что это займет около 10 (10) секунд. Реалистично, мы знаем, что это будет немного хуже, чем предсказывает Big O Notation, потому что операция O(n) потребует много операций O(1) для окупаемости.

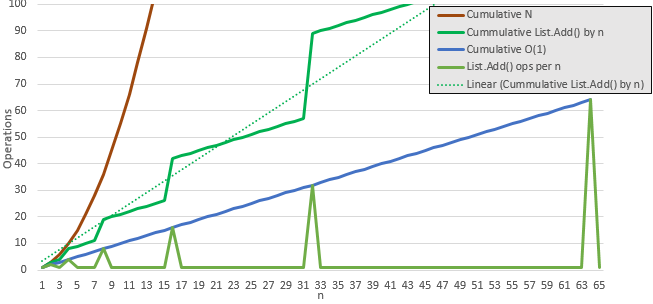
увеличено, вы можете увидеть, как кумулятивные операции зависят от списка.Копировать() First 65 n by Cumulative Operation Count

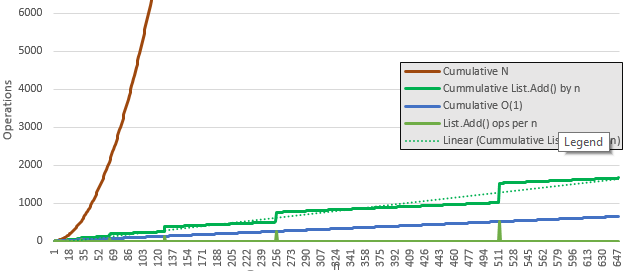
увеличенный, вы видно, что это не влияет на масштаб по сравнению с операцией O(n). First 650 n by Cumulative Operation Count

stackToList (stack, false)= O (n^2). Функция insert списка выполняет копию массива, которая должна переместить все элементы списка в новый список. Когда указатель начинает итерацию через родительский стек, количество операций начинается с 0, а затем растет до тех пор, пока не достигнет n. В среднем это происходит n / 2 раза. Константа 2 удаляется в Большое обозначение O, и вы остаетесь с n. Учитывая отсутствие узких мест в ресурсах, если этот алгоритм завершается за 10 секунд с 10 миллионами элементов, чтобы завершить 100 миллионов элементов, вы ожидаете, что это займет около 10 (10^2) секунд. Реально, мы знаем, что второй случай будет масштабироваться лучше, чем предсказывает Big O Notation, потому что на самом деле это n*(n-1), но он не будет масштабироваться лучше, чем O(n*Log(n)), следующий шаг вниз. Descending Operation Comparison

сломать Операции:

List<int> stackToList(Stack<int> stack, bool reverseOrder) {
    List<int> items = new List<int>(); // O(1)

    while (stack.Count > 0) {        //  O(n): For every int in the supplied stack
        int item = stack.Pop();        // O(1): https://referencesource.microsoft.com/#System/compmod/system/collections/generic/stack.cs,222

        if (reverseOrder) {            // O(1)
            items.Insert(0, item);     // O(n^2): https://referencesource.microsoft.com/#mscorlib/system/collections/generic/list.cs,669
        } else {
            items.Add(item);           // O(Slightly more than 1): https://referencesource.microsoft.com/#mscorlib/system/collections/generic/list.cs,220
        }
    }
    return items;
}
0