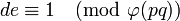Создание закрытого ключа RSA в C#

у меня есть значения для p, q, n и e и хотел бы рассчитать закрытый ключ d. Как я могу это сделать, может кто-нибудь дать мне пример кода C#? Я использую BigInteger класс для представления значений для p, q, n и e поэтому я предполагаю, что d будет BigInteger как хорошо.

6
c# cryptography encryption rsa

3 ответов

короткий способ-вычислить обратный e дулю (С-1)*(q-1). На самом деле вам нужно только наименее распространенное кратное p-1 и q-1, но это не купит вам много (да, есть несколько возможных значений для d, это нормально, все они эквивалентны).

Если BigInteger класс имеет модульный обратный метод, тогда это будет легко: просто вызовите его. В противном случае, вам придется вычислить его самостоятельно, использование расширенного евклидова алгоритма (это то, что BigInteger классы, как правило, используются для вычисления модульных инверсий).

1

С Википедия:

определите d (используя модульную арифметику), который удовлетворяет соотношению конгруэнтности alt text

  • заявленный по-разному, ed - 1 может быть равномерно разделен totient (p - 1)(q-1).
  • это часто вычисляется с использованием расширенного евклидова алгоритма.
  • d хранится как показатель закрытого ключа.

расширенный евклидов алгоритм позволяет найти целые числа, такие что выполняется следующее:

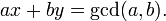
alt text

расширенный евклидов алгоритм особенно полезен, когда a и b являются coprime, так как x является модульным мультипликативным обратным по модулю b.

в этом наборе формул a to e, b to (p-1)(q-1) и gcd(a, b) до 1(потому что e и φ (pq) должны быть coprime в алгоритме RSA) и решить для x что дает вам ваш d. Страница Википедии на расширенный алгоритм Евклида имеет более подробную информацию о том, как написать алгоритм для решения для x и y. Например, вы можете использовать эту рекурсивную функцию (в псевдокоде):

function extended_gcd(a, b)
    if a mod b = 0
        return {0, 1}
    else
        {x, y} := extended_gcd(b, a mod b)
        return {y, x-(y*(a div b))}

в .NET если вы просто хотите создать некоторые ключи RSA, вам не нужно реализовывать алгоритм RSA самостоятельно. В .NET framework уже есть реализация RSA, которую можно использовать.

3

вот как я это сделал.

простые числа p=7 и q=17

вычислить n = p*q = 119

вычислить f (n) = (p-1)*(q-1) = 96

вычислить d = e^-1 mod f (n), например, d = 77

1