Создать матрицу корреляции с векторной корреляции в R
Я хочу создать корреляционную матрицу с учетом корреляционного вектора, который является верхней (или нижней) треугольной матрицей корреляционной матрицы.
цель состоит в том, чтобы преобразовать этот вектор
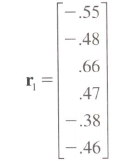
к этой корреляционной матрице с 1s по диагонали.
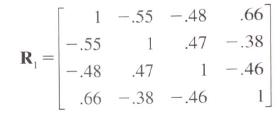
знаете ли вы, есть ли метод создания матрицы, заданной треугольной над диагональю и установить диагональ в 1?
4 ответов
Я не знаю, есть ли автоматический способ сделать это, но расширяя мой комментарий:
myvec <- c(-.55, -.48, .66, .47, -.38, -.46)
mempty <- matrix(0, nrow = 4, ncol = 4)
mindex <- matrix(1:16, nrow = 4, ncol = 4)
mempty[mindex[upper.tri(mindex)]] <- myvec
mempty[lower.tri(mempty)] <- t(mempty)[lower.tri(t(mempty))]
diag(mempty) <- 1
mempty
# [,1] [,2] [,3] [,4]
# [1,] 1.00 -0.55 -0.48 0.47
# [2,] -0.55 1.00 0.66 -0.38
# [3,] -0.48 0.66 1.00 -0.46
# [4,] 0.47 -0.38 -0.46 1.00
вот быстро набросал функцию. Надеюсь, все мои математические шаги верны!
vec2symmat <- function(invec, diag = 1, byrow = TRUE) {
Nrow <- ceiling(sqrt(2*length(invec)))
if (!sqrt(length(invec)*2 + Nrow) %% 1 == 0) {
stop("invec is wrong length to create a square symmetrical matrix")
}
mempty <- matrix(0, nrow = Nrow, ncol = Nrow)
mindex <- matrix(sequence(Nrow^2), nrow = Nrow, ncol = Nrow, byrow = byrow)
if (isTRUE(byrow)) {
mempty[mindex[lower.tri(mindex)]] <- invec
mempty[lower.tri(mempty)] <- t(mempty)[lower.tri(t(mempty))]
} else {
mempty[mindex[upper.tri(mindex)]] <- invec
mempty[lower.tri(mempty)] <- t(mempty)[lower.tri(t(mempty))]
}
diag(mempty) <- diag
mempty
}
здесь он имеет другое значение для диагонали.
vec2symmat(1:3, diag = NA)
# [,1] [,2] [,3]
# [1,] NA 1 2
# [2,] 1 NA 3
# [3,] 2 3 NA
вот сообщение об ошибке, если вы пытаетесь предоставить данные, которые не могут создать квадратную матрицу.
vec2symmat(1:4)
# Error in vec2symmat(1:4) :
# invec is wrong length to create a square symmetrical matrix
и, с настройками по умолчанию.
vec2symmat(1:10)
# [,1] [,2] [,3] [,4] [,5]
# [1,] 1 1 2 3 4
# [2,] 1 1 5 6 7
# [3,] 2 5 1 8 9
# [4,] 3 6 8 1 10
# [5,] 4 7 9 10 1
вы можете убедить R, что ваш вектор является объектом расстояния, а затем использовать as.matrix преобразовать это:
> myvec <- c(-.55, -.48, .66, .47, -.38, -.46)
> class(myvec) <- 'dist'
> attr(myvec,'Size') <- 4
> as.matrix(myvec)
1 2 3 4
1 0.00 -0.55 -0.48 0.66
2 -0.55 0.00 0.47 -0.38
3 -0.48 0.47 0.00 -0.46
4 0.66 -0.38 -0.46 0.00
или вариация на ответ @AnandaMahto (аналогично внутренностям, используемым выше):
> myvec <- c(-.55, -.48, .66, .47, -.38, -.46)
> mycor <- matrix(0,4,4)
> mycor[ col(mycor) < row(mycor) ] <- myvec
> mycor <- mycor + t(mycor)
> diag(mycor) <- 1
> mycor
[,1] [,2] [,3] [,4]
[1,] 1.00 -0.55 -0.48 0.66
[2,] -0.55 1.00 0.47 -0.38
[3,] -0.48 0.47 1.00 -0.46
[4,] 0.66 -0.38 -0.46 1.00
ответ с некоторыми вспомогательными функциями, которые могут быть полезны в других проблемах:
`lower.tri<-` <- function(x,value){
x[lower.tri(x)] <- value
x
}
`upper.tri<-` <- function(x,value){
y <- t(x)
lower.tri(y) <- value
t(y)
}
vec2mat <- function(r){
n <- (1+sqrt(1+8*length(r)))/2
x <- diag(1,n)
lower.tri(x) <- upper.tri(x) <- r
x
}
EDIT: обратите внимание, что upper.tri<- не просто получается, заменяя "нижний" на "верхний" в lower.tri<-. Это сделало бы результат несимметричным.
результат:
vec2mat(c(-0.55, -0.48, 0.66, 0.47, -0.38, -0.46))
[,1] [,2] [,3] [,4]
[1,] 1.00 -0.55 -0.48 0.66
[2,] -0.55 1.00 0.47 -0.38
[3,] -0.48 0.47 1.00 -0.46
[4,] 0.66 -0.38 -0.46 1.00
на любом языке программирования я думаю, что вы просто сделаете это с парой вложенных циклов for следующим образом:
дано:
вектор R; / / я буду использовать круглые скобки R(3) для обозначения третьего элемента. // (который хранится в ячейке памяти R[2] на языках с нулевыми массивами) int N;
Matrix M=Matrix (N,N); // новый экземпляр вашего матричного объекта, или вы можете просто использовать массивы.
int i,j,k;
k=1;
for(i=1;i<N;i++)
{
M(i,i)=1;
for(j=i+1,j<=N;j++)
{
M(i,j)=M(j,i)=R[k];
k=k+1;
}
}
Здесь I предполагается, что вы знаете, что такое N, и что у вас есть базовые объекты, такие как векторы и матрицы. (Если нет, это отличная проблема для написания ваших первых "объектов") сложные структуры данных, такие как векторы, матрицы, комплексные числа и гистограммы, делают идеальные объекты. Правильный способ думать об объектно-ориентированном программировании для научной работы - использовать объекты, чтобы научить компилятор понимать типы данных высокого уровня, которые вы хотите использовать в своей реальной работе... Этот объекты используются для создания пользовательского языка программирования, идеально подходящего для вашего типа работы. Все, что обычно полезно, должно входить в объект, так как эти объекты будут расти и развиваться, чтобы стать вашей многоразовой базой кода.
код верхнего уровня может быть либо очень мощным, легко читаемым и чистым приложением (так как большая часть подробной работы выполняется в объектах), либо, для быстрого и грязного кодирования, код верхнего уровня-это то, где вы помещаете все хрупкие хаки. Поскольку он не предназначен для повторного использования.
Как только вы получили что-то вроде этого отлаженного, вы просто сделаете конструктор матрицы, который принимает вектор корреляции и N в качестве аргументов и инициализирует матрицу для вас.
конечно, если вы используете некоторую графическую математическую программу высокого уровня, которая имеет сильные мнения о том, что вы можете и не можете делать с матрицами и векторами, тогда вам придется умножить вектор на N матриц для генерации каждого из векторов столбцов выпускной экзамен. (или прочитайте руководство)
по крайней мере, вы должны сказать нам, как называется математическая программа... :)
