Создать матрицу смежности для взвешенного графа
Я пытаюсь реализовать Флойд-Warshall Алгоритм. Для этого мне нужно настроить adjacency matrix взвешенного графа. Как мне это сделать? Я знаю значения и приложил изображение взвешенного графика. Я попытался найти некоторые онлайн-примеры этого, но я ничего не могу найти. Я понимаю алгоритм Флойда-Уоршелла, мне просто нужна помощь в его настройке, чтобы я мог его реализовать. Вот один, который я построил раньше, но я не сделал должны использовать определенные значения.
код:
public static void buildAdjMatrix()
{
for (int i = 0; i < 100; i++)
{
for (int j = 0; j < 100; j++)
{
if (directionAllowed(i, j) == true)
{
adjMatrix[i, j] = 1;
}
else
{
adjMatrix[i, j] = 50;
}
}
}
}
вот конкретный график под рукой:
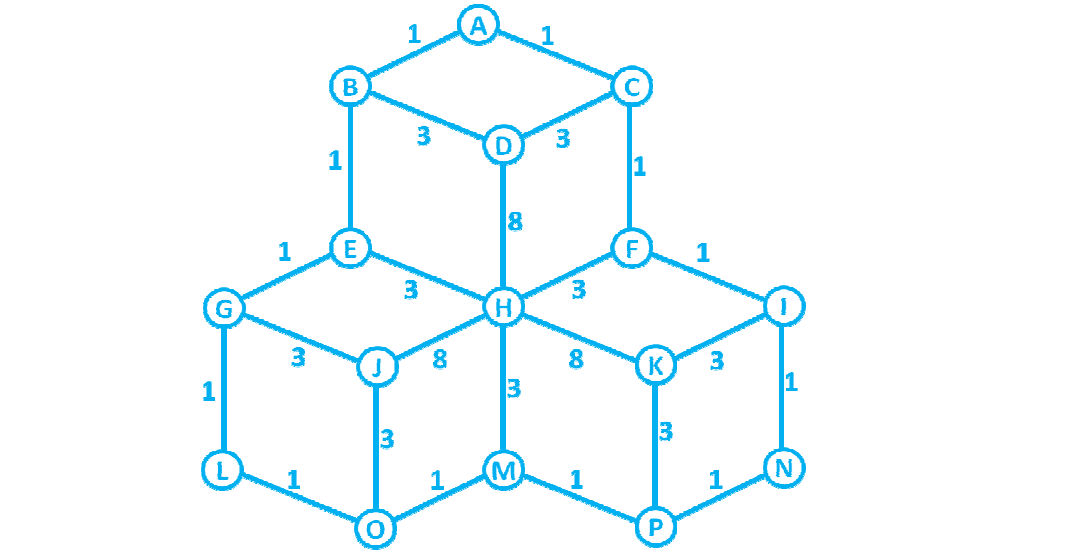
вот изображение матрицы, которую мне нужно создать.. Извините за ужасное качество...

1 ответов
Итак, вы, кажется, не знакомы с графы, взгляните на Википедию. Также просмотрите некоторые изображения, это становится легче понять.
немного понятие
ваша фотография может быть представлена как Graph. Как правило, графики реализуются с использованием 2 основных видов элементов,Nodes и Links (иногда называют Arcs).
A Node обозначают буквы в твоей картинке, они будут А, B, C и т. д.
Ан Arc или Link, это линия, соединяющая два узла, если вы посмотрите связь между H и L, у них есть связь между ними, в взвешенном графике разные связи имеют разные веса.
решение вашей проблемы - Часть 1
то, что мы должны сделать, это представить вашу картину в виде графика в коде, так что давайте начнем создавать основные элементы Node и Arc:
узел
узел имеет Name, поэтому мы можем определить узел. И узел может быть подключен к другим узлам, мы могли бы использовать коллекцию узлов, но ваш-взвешенный график, поэтому каждое из соединений должно быть представлено связанным узлом и его весом. Поэтому мы используем коллекцию Дуг.
public class Node
{
public string Name;
public List<Arc> Arcs = new List<Arc>();
public Node(string name)
{
Name = name;
}
/// <summary>
/// Create a new arc, connecting this Node to the Nod passed in the parameter
/// Also, it creates the inversed node in the passed node
/// </summary>
public Node AddArc(Node child, int w)
{
Arcs.Add(new Arc
{
Parent = this,
Child = child,
Weigth = w
});
if (!child.Arcs.Exists(a => a.Parent == child && a.Child == this))
{
child.AddArc(this, w);
}
return this;
}
}
Arc
действительно простой класс, он содержит связанные узлы и вес соединения:
public class Arc
{
public int Weigth;
public Node Parent;
public Node Child;
}
графика
Graph-это своего рода обертка класс, для целей организации. Я также объявил корень для графика, мы его не используем, но полезно в нескольких случаях:
public class Graph
{
public Node Root;
public List<Node> AllNodes = new List<Node>();
public Node CreateRoot(string name)
{
Root = CreateNode(name);
return Root;
}
public Node CreateNode(string name)
{
var n = new Node(name);
AllNodes.Add(n);
return n;
}
public int?[,] CreateAdjMatrix()
{
// Matrix will be created here...
}
}
решение вашей проблемы-Часть 2
теперь у нас есть вся структура данных для хранения графика, давайте заполним его некоторыми данными. Вот код, который инициализирует график, похожий на изображение Куба. Это скучно и скучно, но в реальных случаях график будет создаваться динамически:
static void Main(string[] args)
{
var graph = new Graph();
var a = graph.CreateRoot("A");
var b = graph.CreateNode("B");
var c = graph.CreateNode("C");
var d = graph.CreateNode("D");
var e = graph.CreateNode("E");
var f = graph.CreateNode("F");
var g = graph.CreateNode("G");
var h = graph.CreateNode("H");
var i = graph.CreateNode("I");
var j = graph.CreateNode("J");
var k = graph.CreateNode("K");
var l = graph.CreateNode("L");
var m = graph.CreateNode("M");
var n = graph.CreateNode("N");
var o = graph.CreateNode("O");
var p = graph.CreateNode("P");
a.AddArc(b, 1)
.AddArc(c, 1);
b.AddArc(e, 1)
.AddArc(d, 3);
c.AddArc(f, 1)
.AddArc(d, 3);
c.AddArc(f, 1)
.AddArc(d, 3);
d.AddArc(h, 8);
e.AddArc(g, 1)
.AddArc(h, 3);
f.AddArc(h, 3)
.AddArc(i, 1);
g.AddArc(j, 3)
.AddArc(l, 1);
h.AddArc(j, 8)
.AddArc(k, 8)
.AddArc(m, 3);
i.AddArc(k, 3)
.AddArc(n, 1);
j.AddArc(o, 3);
k.AddArc(p, 3);
l.AddArc(o, 1);
m.AddArc(o, 1)
.AddArc(p, 1);
n.AddArc(p, 1);
// o - Already added
// p - Already added
int?[,] adj = graph.CreateAdjMatrix(); // We're going to implement that down below
PrintMatrix(ref adj, graph.AllNodes.Count); // We're going to implement that down below
}
решении ваших проблема - Часть 3
Итак, у нас есть полностью инициализированный граф, давайте создадим матрицу. Следующий метод создает матрицу двух измерений, N на n, где n-количество узлов, которые мы получаем из класса graph. Для поиска узлов, если у них есть ссылка, Если у них есть ссылка, заполненная матрица в соответствующем положении. Посмотрите, что в вашем примере матрицы смежности у вас есть только 1s, Здесь я кладу вес ссылки, я положил этот путь, так что нет смысла в имея взвешенный график!
public int?[,] CreateAdjMatrix()
{
int?[,] adj = new int?[AllNodes.Count, AllNodes.Count];
for (int i = 0; i < AllNodes.Count; i++)
{
Node n1 = AllNodes[i];
for (int j = 0; j < AllNodes.Count; j++)
{
Node n2 = AllNodes[j];
var arc = n1.Arcs.FirstOrDefault(a => a.Child == n2);
if (arc != null)
{
adj[i, j] = arc.Weigth;
}
}
}
return adj;
}
сделал
это сделано, у вас есть взвешенная матрица смежности, каким-то образом ее распечатать:
private static void PrintMatrix(ref int?[,] matrix, int Count)
{
Console.Write(" ");
for (int i = 0; i < Count; i++)
{
Console.Write("{0} ", (char)('A' + i));
}
Console.WriteLine();
for (int i = 0; i < Count; i++)
{
Console.Write("{0} | [ ", (char)('A' + i));
for (int j = 0; j < Count; j++)
{
if (i == j)
{
Console.Write(" &,");
}
else if (matrix[i, j] == null)
{
Console.Write(" .,");
}
else
{
Console.Write(" {0},", matrix[i, j]);
}
}
Console.Write(" ]\r\n");
}
Console.Write("\r\n");
}
что дает нам следующий выход:
A B C D E F G H I J K L M N O P
A | [ &, 1, 1, ., ., ., ., ., ., ., ., ., ., ., ., ., ]
B | [ 1, &, ., 3, 1, ., ., ., ., ., ., ., ., ., ., ., ]
C | [ 1, ., &, 3, ., 1, ., ., ., ., ., ., ., ., ., ., ]
D | [ ., 3, 3, &, ., ., ., 8, ., ., ., ., ., ., ., ., ]
E | [ ., 1, ., ., &, ., 1, 3, ., ., ., ., ., ., ., ., ]
F | [ ., ., 1, ., ., &, ., 3, 1, ., ., ., ., ., ., ., ]
G | [ ., ., ., ., 1, ., &, ., ., 3, ., 1, ., ., ., ., ]
H | [ ., ., ., 8, 3, 3, ., &, ., 8, 8, ., 3, ., ., ., ]
I | [ ., ., ., ., ., 1, ., ., &, ., 3, ., ., 1, ., ., ]
J | [ ., ., ., ., ., ., 3, 8, ., &, ., ., ., ., 3, ., ]
K | [ ., ., ., ., ., ., ., 8, 3, ., &, ., ., ., ., 3, ]
L | [ ., ., ., ., ., ., 1, ., ., ., ., &, ., ., 1, ., ]
M | [ ., ., ., ., ., ., ., 3, ., ., ., ., &, ., 1, 1, ]
N | [ ., ., ., ., ., ., ., ., 1, ., ., ., ., &, ., 1, ]
O | [ ., ., ., ., ., ., ., ., ., 3, ., 1, 1, ., &, ., ]
P | [ ., ., ., ., ., ., ., ., ., ., 3, ., 1, 1, ., &, ]
