Создать непересекающийся многоугольник, проходящий через все заданные точки
предположим, что у меня есть массив точек в случайном порядке, и мне нужно найти многоугольник (сортируя их, так что каждая соседняя пара представляет собой сторону), который проходит через все точек, и его стороны, конечно, не пересекаются.
Я попытался сделать это, выбрав точку и добавив все точки в конечный массив, которые находятся ниже нее, отсортированы слева направо. Затем, добавив все точки, которые находятся над ним, отсортируйте справа налево.
Мне сказали что я могу добавить дополнительную точку и сортировать естественно, чтобы избежать самопересечений.. Но я не могу этого понять. Какой простой способ сделать это?
7 ответов
как кто-то сказал, минимальное решение длины-это именно проблема коммивояжера. Вот неоптимальный, но осуществимый подход:
вычислить Делоне триангуляция ваших очков. Последовательно удаляйте граничные сегменты, пока не останется граница, которая интерполирует все точки или не может быть удалено больше сегментов. Не удаляйте граничные сегменты, если все точки треугольника, использующие этот сегмент, находятся на границе. Возьмите эту границу как свою путь.
я реализовал это в Mathematica, используя 40 случайных точек. Вот типичный результат:
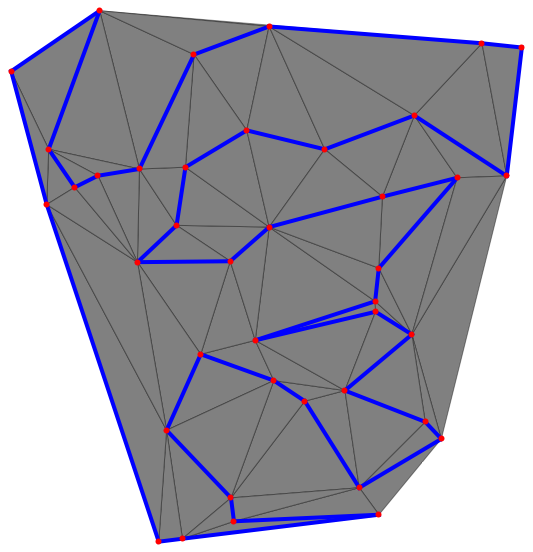
очевидное возражение заключается в том, что вы можете добраться до точки, где не все ваши точки являются граничными точками, но вы не можете удалить граничный сегмент, не сделав границу само пересекающейся. Это обоснованное возражение. Мне потребовались десятки пробежек, чтобы увидеть случай, где это произошло, но, наконец, получил это дело:
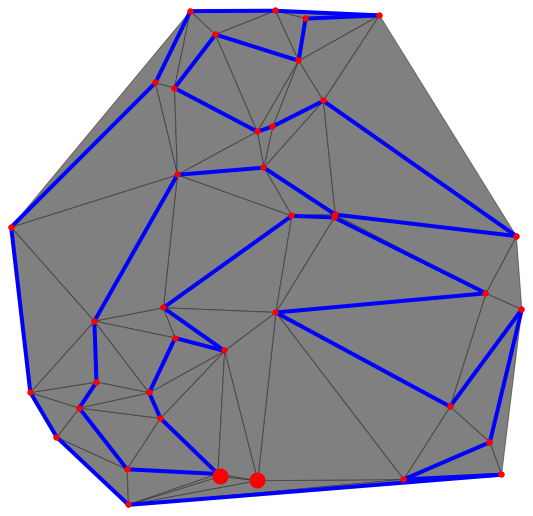
вы, вероятно, можете увидеть некоторые очевидные способы исправления этого с помощью локальной топологии, но я оставлю детали вам! Единственное, что может помочь-это "мелькание краев" где вы берете двух треугольников, которые имеют общую сторону, скажем треугольник (Р,Q,р) и (Q,р,S) и заменить их (р,п,S) и (р,х,м) (все координаты в направлении против часовой стрелки вокруг треугольника). Это можно сделать до тех пор, пока результирующие треугольники в этом преобразовании также упорядочены против часовой стрелки.
для уменьшения потребности для Починок, вы будете хотеть делать хороший выбор сегментов для удаления на каждом этапе. Я использовал отношение длины граничного сегмента к сумме длин другой стороны треугольника-кандидата (треугольника, образованного потенциально входящей точкой с сегментом).
наша стратегия состоит в том, чтобы составить план, в котором мы уверены, что многоугольник включает в себя все точки, и что мы можем найти порядок их подключения где ни одна из линий не пересекаются.
алгоритм:
1. Найдите самые левые точки p
2. Найдите самую правую точку q
3. Разделите точки На A, набор точек ниже pq и B, набор точек выше pq [вы можете использовать тест поворота влево (p, q,?) к определить, является ли точка над линией.]
4. Сортировка по координате x (увеличение)
5. Сортировка B по координате x (уменьшение).
6. Верните многоугольник, определенный p, точки в A, в порядке, q, точки B в порядке.время работы:
Шаги 1,2,3 занимают O (n) времени.
Шаги 4,5 занимают O (nlogn) времени.
Шаг 6 Возьмите O (n) время.
Общее время выполнения-O (nlogn).достоверность:
По конструкции все точки помимо p, q находятся в множестве A или набор B. наш выходной многоугольник из строки 6 поэтому выводит многоугольник с все точки. Теперь нам нужно утверждать, что ни один из сегментов линии в наши выходные полигоны пересекаются.рассмотрим каждый сегмент в выходной полигон. Первый край от p до первой точки в A не может пересеките любой сегмент (потому что сегмента еще нет). Как мы исходим в порядке по координате x через точки в A из каждой точки следующий сегмент идет вправо, а все предыдущие сегменты левый. Таким образом, по мере продвижения от p через все точки A к точке q, у нас не будет перекрестков.
то же самое верно, как мы идем от Q обратно через точки B. эти сегменты не могут пересекаться друг с другом потому что они идут справа налево. Эти сегменты также не могут пересекать что-либо в A, потому что все точки в A находятся ниже линии pq, и все точки B находятся выше этой линии.
таким образом, сегменты не пересекаются друг с другом другие и у нас есть простой многоугольник.
источник:http://www.cs.wustl.edu/~pless/546/homeworks / hw1_selectedProblems.pdf
Я понимаю, что это очень поздно, но это может быть полезно для будущих зрителей.
то, что вы ищете называется простой полигонизация в литературе. См., например, этой странице по теме. Легко генерировать звезды полигонизация, как говорит Мигель, но трудно найти, например, минимальную полигонизацию периметра, которая является минимальной TSP, как упоминает Аксель Кемпер. В общем случае существует экспоненциальное число различных полигонизаций для данной точки набор.
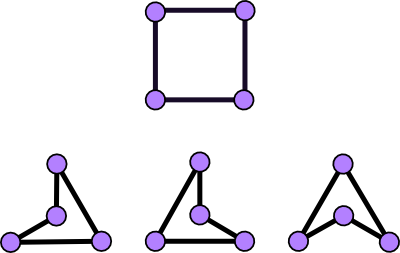
для звездообразной полигонизации есть одна проблема, которая требует некоторого внимания: дополнительная точка x (в" ядре " звезды) не должно совпадать с существующей точкой! Вот один алгоритм, чтобы гарантировать x. Найти ближайшую пару точек (a, b), и пусть x быть серединой сегмента ab. Тогда действуйте в соответствии с должностью Мигеля.
Ну, если вы на самом деле не заботитесь о минимальности или что-то в этом роде, вы можете просто поместить новую точку внутри выпуклой оболочки, а затем упорядочить другие точки под углом к этой новой точке. Вы получите непересекающийся многоугольник.
тестирование, если два сегмента пересекаются просто и быстро. См.это например.
С этим вы можете построить свой многоугольник итеративно:
Источник Пунктах : S = {S0, ... Si, Sj,...}
Полигон : A = {A0, ... Ai, Aj,...}
вы начинаете с S полных и A пустой.
возьмите первые 3 очка S и переместите их в A. Этот треугольник, конечно, не пересекается сам с собой.
потом, пока S пусто, возьмите его первую оставшуюся точку, которую мы назовем P, и искать позицию в A где его можно вставить.
эта позиция i+1 первый i проверка того, что ни [Ai-P], ни [Ai+1-P] пересекает любые другие сегменты [Ak-Ak+1].
ваш новый полигон - это {A0, ... Ai, P, Ai+1, ...}
вот код python 3.6 (требуются библиотеки: matplotlib, numpy) на основе bdean20 ' s ответ.
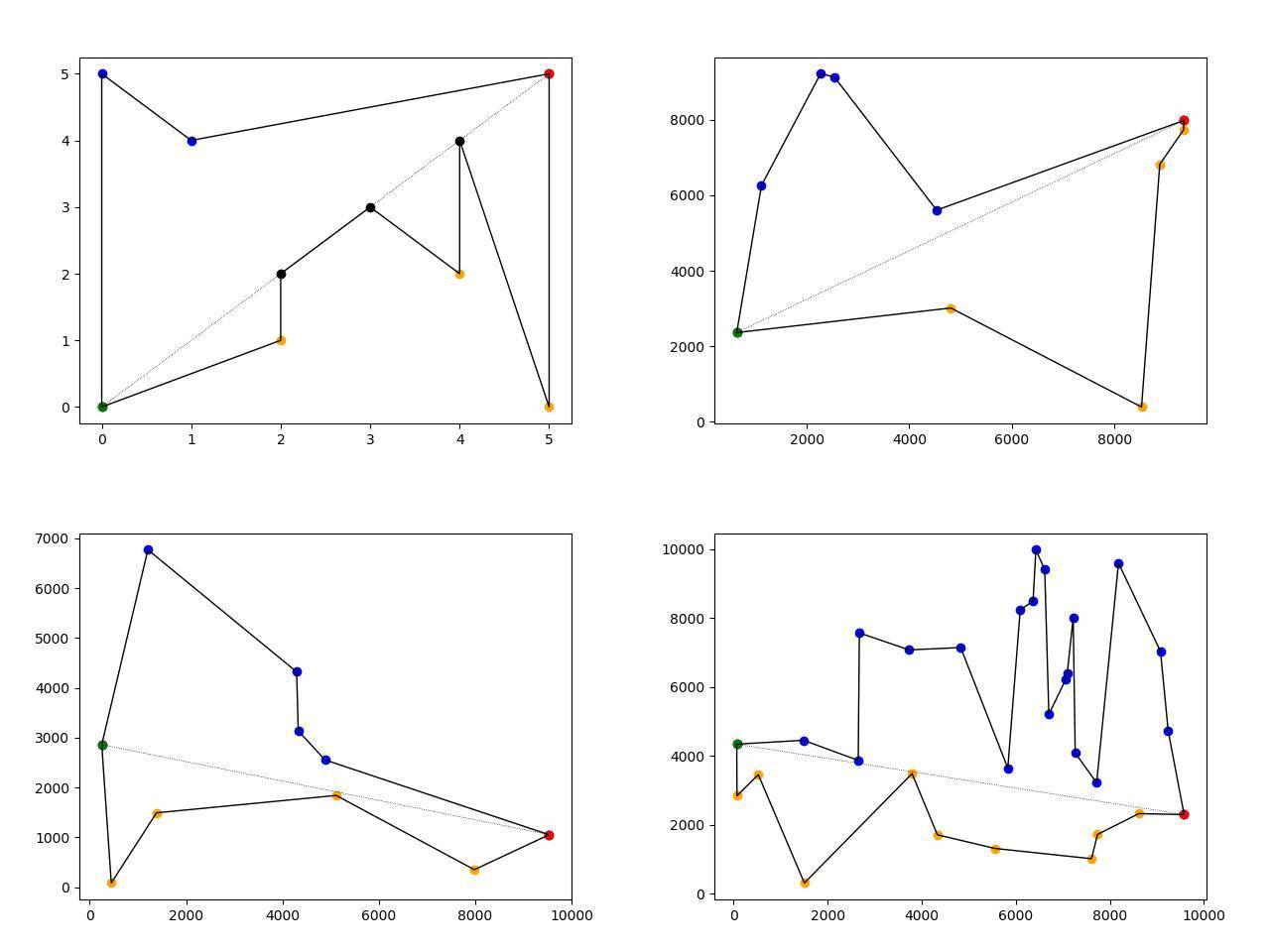
Фото Описание:
- вверху слева-предопределенные полигоны, другие полигоны генерируются случайным образом.
- пунктирная линия-соединяет зеленый (самый левый) и красный (самый правый) полигоны точки.
- черные точки лежат на пунктирной линии.
- Оранжевые точки лежат ниже пунктирных линия.
- синие точки лежат над пунктирной линией.
=========
import random
from operator import itemgetter
import numpy
import matplotlib
import matplotlib.pyplot
class Create_random_polygon:
def __init__(self, array, min_rand_coord = None, max_rand_coord = None, points_num = None):
self.array = array
self.min_rand_coord = min_rand_coord
self.max_rand_coord = max_rand_coord
self.points_num = points_num
def generate_random_points(self):
random_coords_list = []
for x in range(self.points_num):
coords_tuple = (random.randint(self.min_rand_coord, self.max_rand_coord),
random.randint(self.min_rand_coord, self.max_rand_coord))
random_coords_list.append(coords_tuple)
self.array = random_coords_list
return random_coords_list
def close_line_to_polygon(self):
a = self.array[0]
b = self.array[len(self.array)-1]
if a == b:
pass
else:
self.array.append(a)
def find_leftmost_point(self):
leftmost_point = None
leftmost_x = None
for point in self.array:
x = point[0]
if leftmost_x == None or x < leftmost_x:
leftmost_x = x
leftmost_point = point
return leftmost_point
def find_rightmost_point(self):
rightmost_point = None
rightmost_x = None
for point in self.array:
x = point[0]
if rightmost_x == None or x > rightmost_x:
rightmost_x = x
rightmost_point = point
return rightmost_point
def is_point_above_the_line(self, point, line_points):
"""return 1 if point is above the line
return -1 if point is below the line
return 0 if point is lays on the line"""
px, py = point
P1, P2 = line_points
P1x, P1y = P1[0], P1[1]
P2x, P2y = P2[0], P2[1]
array = numpy.array([
[P1x - px, P1y - py],
[P2x - px, P2y - py],
])
det = numpy.linalg.det(array)
sign = numpy.sign(det)
return sign
def sort_array_into_A_B_C(self, line_points):
[(x_lm, y_lm), (x_rm, y_rm)] = line_points
A_array, B_array, C_array = [], [], []
for point in self.array:
x, y = point
sing = self.is_point_above_the_line( (x, y), line_points)
if sing == 0:
C_array.append(point)
elif sing == -1:
A_array.append(point)
elif sing == 1:
B_array.append(point)
return A_array, B_array, C_array
def sort_and_merge_A_B_C_arrays(self, A_array, B_array, C_array):
A_C_array = [*A_array, *C_array]
A_C_array.sort(key=itemgetter(0))
B_array.sort(key=itemgetter(0), reverse=True)
merged_arrays = [*A_C_array, *B_array]
self.array = merged_arrays
def show_image(self, array, line_points, A_array, B_array, C_array):
[(x_lm, y_lm), (x_rm, y_rm)] = line_points
x = [x[0] for x in array]
y = [y[1] for y in array]
Ax = [x[0] for x in A_array]
Ay = [y[1] for y in A_array]
Bx = [x[0] for x in B_array]
By = [y[1] for y in B_array]
Cx = [x[0] for x in C_array]
Cy = [y[1] for y in C_array]
matplotlib.pyplot.plot(Ax, Ay, 'o', c='orange') # below the line
matplotlib.pyplot.plot(Bx, By, 'o', c='blue') # above the line
matplotlib.pyplot.plot(Cx, Cy, 'o', c='black') # on the line
matplotlib.pyplot.plot(x_lm, y_lm, 'o', c='green') # leftmost point
matplotlib.pyplot.plot(x_rm, y_rm, 'o', c='red') # rightmost point
x_plot = matplotlib.pyplot.plot([x_lm, x_rm], [y_lm, y_rm], linestyle=':', color='black', linewidth=0.5) # polygon's division line
x_plot = matplotlib.pyplot.plot(x, y, color='black', linewidth=1) # connect points by line in order of apperiance
matplotlib.pyplot.show()
def main(self, plot = False):
'First output is random polygon coordinates array (other stuff for ploting)'
print(self.array)
if self.array == None:
if not all(
[isinstance(min_rand_coord, int),
isinstance(max_rand_coord, int),
isinstance(points_num, int),]
):
print('Error! Values must be "integer" type:', 'min_rand_coord =',min_rand_coord, ', max_rand_coord =',max_rand_coord, ', points_num =',points_num)
else:
self.array = self.generate_random_points()
print(self.array)
x_lm, y_lm = self.find_leftmost_point()
x_rm, y_rm = self.find_rightmost_point()
line_points = [(x_lm, y_lm), (x_rm, y_rm)]
A_array, B_array, C_array = self.sort_array_into_A_B_C(line_points)
self.sort_and_merge_A_B_C_arrays(A_array, B_array, C_array)
self.close_line_to_polygon()
if plot:
self.show_image(self.array, line_points, A_array, B_array, C_array)
return self.array
if __name__ == "__main__":
# predefined polygon
array = [
(0, 0),
(2, 2),
(4, 4),
(5, 5),
(0, 5),
(1, 4),
(4, 2),
(3, 3),
(2, 1),
(5, 0),
]
array = None # no predefined polygon
min_rand_coord = 1
max_rand_coord = 10000
points_num = 30
crt = Create_random_polygon(array, min_rand_coord, max_rand_coord, points_num)
polygon_array = crt.main(plot = True)
==========
Я считаю, что вы можете использовать Грэхема алгоритм для решения вашей проблемы.
Edit: в общем, алгоритмы выпуклой оболочки есть на что посмотреть.
