Способ построения равноудаленной кривой
Я написал этот вопрос на mathoverflow, но я хочу знать Ваше мнение об этом также. Я хочу нарисовать кривую, которая всегда находится на определенном расстоянии от нормали к поверхности данной кривой. Я знаю формулу данной кривой (кусочно-кубический сплайн). Проблема, по - видимому, заключается в том, что расстояние отклонения больше радиуса кривой-точки скремблируются. Кто-нибудь сталкивался с такой проблемой. Есть хороший решение?
Спасибо за любые идеи,
Юлиан
позже: проблема прекрасно описана ниже г-ном мастером.
2 ответов
EDIT:Примечание: этот ответ не об избежании угловой обертки (что является особенностью строгих равноудаленных кривых).
по данным Википедия,
кривая с фиксированным смещением от заданной кривой Безье, часто называемая кривой смещения (лежащая "параллельно" исходной кривой, как смещение между рельсами на железнодорожном пути), не может быть точно сформирована кривой Безье (за исключением некоторых тривиальных случаев). Тем не менее, есть эвристические методы, которые обычно дают адекватное приближение для практических целей.
Итак, есть эвристические методы, которые вам придется использовать, чтобы получить приближение. Есть научная статья под названием сравнение методов аппроксимации кривых смещения включая сравнение 9 алгоритмов.
Если вы хотите пропустить исследований и просто получить решение, взгляните на это сообщение в блоге, описывающее реализацию алгоритм де Кастельжо это. EDIT: я должен признать, что я не уверен, как эта реализация ведет себя с резкими поворотами.
Я думаю, вы столкнетесь с проблемой с вашим определением:"... нарисуйте кривую, которая всегда находится на определенном расстоянии от нормали к поверхности заданной кривой."
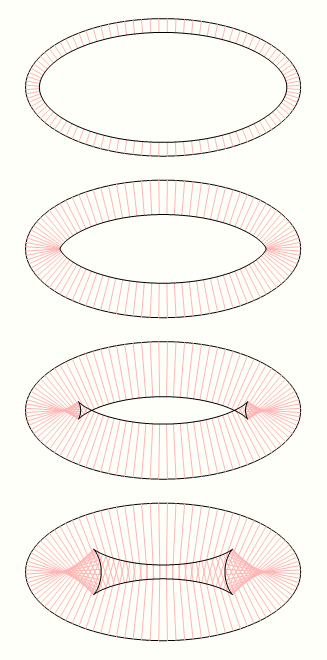
Если вы нарисуете серию линий внутри вогнутой кривой, в какой-то момент линия будет складываться обратно на себя, в конечном итоге создавая геометрическую инверсию.
применяется к эллипсу, например: