Способ равномерного случайного заполнения диска точками в python
У меня есть приложение, которое требует диска, заполненного точками " n " квази-случайным образом. Я хочу, чтобы точки были несколько случайными, но все же имели более или менее регулярную плотность над диском.
мой текущий метод-разместить точку, проверить, находится ли она внутри диска, а затем проверить, достаточно ли она удалена от всех других точек, которые уже сохранены. Мой код ниже:
import os
import random
import math
# ------------------------------------------------ #
# geometric constants
center_x = -1188.2
center_y = -576.9
center_z = -3638.3
disk_distance = 2.0*5465.6
disk_diam = 5465.6
# ------------------------------------------------ #
pts_per_disk = 256
closeness_criteria = 200.0
min_closeness_criteria = disk_diam/closeness_criteria
disk_center = [(center_x-disk_distance),center_y,center_z]
pts_in_disk = []
while len(pts_in_disk) < (pts_per_disk):
potential_pt_x = disk_center[0]
potential_pt_dy = random.uniform(-disk_diam/2.0, disk_diam/2.0)
potential_pt_y = disk_center[1]+potential_pt_dy
potential_pt_dz = random.uniform(-disk_diam/2.0, disk_diam/2.0)
potential_pt_z = disk_center[2]+potential_pt_dz
potential_pt_rad = math.sqrt((potential_pt_dy)**2+(potential_pt_dz)**2)
if potential_pt_rad < (disk_diam/2.0):
far_enough_away = True
for pt in pts_in_disk:
if math.sqrt((potential_pt_x - pt[0])**2+(potential_pt_y - pt[1])**2+(potential_pt_z - pt[2])**2) > min_closeness_criteria:
pass
else:
far_enough_away = False
break
if far_enough_away:
pts_in_disk.append([potential_pt_x,potential_pt_y,potential_pt_z])
outfile_name = "pt_locs_x_lo_"+str(pts_per_disk)+"_pts.txt"
outfile = open(outfile_name,'w')
for pt in pts_in_disk:
outfile.write(" ".join([("%.5f" % (pt[0]/1000.0)),("%.5f" % (pt[1]/1000.0)),("%.5f" % (pt[2]/1000.0))])+'n')
outfile.close()
чтобы получить самую четную плотность точек, то, что я делаю, в основном итеративно запустите этот сценарий, используя другой сценарий, с критериями "близости", уменьшенными для каждой последующей итерации. В какой-то момент скрипт не может закончиться, и я просто использую точки последней успешной итерации.
Итак, мой вопрос довольно широк: есть ли лучший способ сделать это? Мой метод пока в порядке, но моя интуиция говорит, что есть лучший способ создать такое поле точек.
иллюстрация выхода показана ниже, одна с высокой близостью критерии, а другой с "самым низким найденным" критерием близости (то, что я хочу).


5 ответов
если у вас есть определенная область, такая как диск (круг), который вы хотите генерировать случайные точки внутри вас, лучше использовать уравнение для круга и ограничить радиус:
x^2 + y^2 = r^2 (0 < r < R)
или параметризовано до двух переменных
cos(a) = x/r
sin(a) = y/r
sin^2(a) + cos^2(a) = 1
чтобы создать что-то вроде псевдослучайного распределения с низкой плотностью, вы должны принять следующий подход:
для случайно распределенных диапазонов r и a выберите n точки.
это позволяет вам генерировать распределение, чтобы примерно соответствовать вашим критериям плотности.
чтобы понять, почему это работает, представьте, что ваш круг сначала разделить на небольшие кольца длиной dr, теперь представьте, что ваш круг разделен на кусочки пирога угла da. Ваша случайность теперь имеет равную вероятность по всей коробчатой области вокруг круга. Если вы разделите области допустимой случайности по всему кругу, вы получите более равномерное распределение вокруг общего круга и небольшого случайного изменения для отдельных областей, дающих вам psudo-случайный взгляд и ощущение, что вы после.
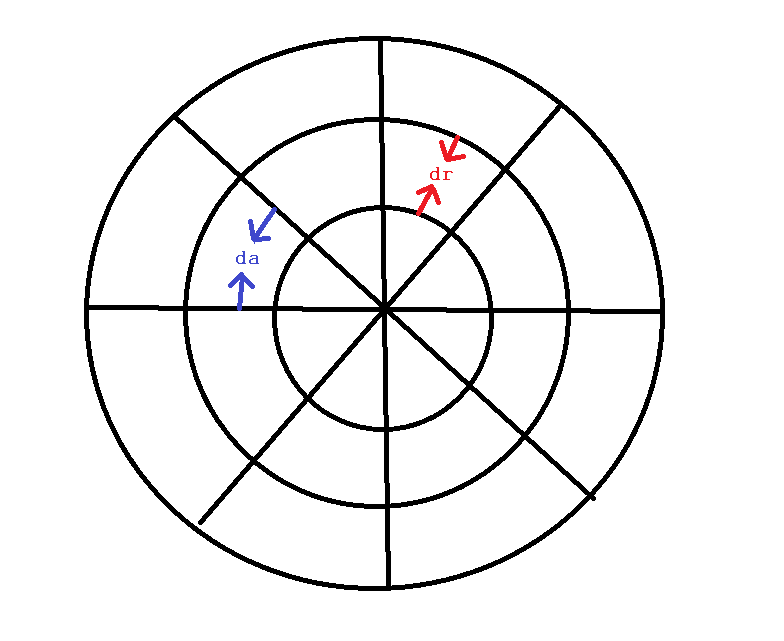
теперь ваша задача просто создать n точки для каждой конкретной территории. Вы захотите иметь n зависит от r как площадь каждого деления изменяется, как вы выходите из круга. Вы можете соразмерить это с точным изменением площади, которое приносит каждое пространство:
для n-го на n+1-го кольца:
d(Area,n,n-1) = Area(n) - Area(n-1)
площадь любого данного кольца:
Area = pi*(dr*n)^2 - pi*(dr*(n-1))
так что разница становится:
d(Area,n,n-1) = [pi*(dr*n)^2 - pi*(dr*(n-1))^2] - [pi*(dr*(n-1))^2 - pi*(dr*(n-2))^2]
d(Area,n,n-1) = pi*[(dr*n)^2 - 2*(dr*(n-1))^2 + (dr*(n-2))^2]
вы объясните это, чтобы получить некоторое представление о том, сколько n должно увеличиваться, но может быть быстрее просто угадать какой-то процент увеличения (30%) или что-то еще.
пример, который я привел, является небольшим подмножеством и уменьшается da и dr значительно улучшится ваш результат.
вот примерный код для генерации таких точек:
import random
import math
R = 10.
n_rings = 10.
n_angles = 10.
dr = 10./n_rings
da = 2*math.pi/n_angles
base_points_per_division = 3
increase_per_level = 1.1
points = []
ring = 0
while ring < n_rings:
angle = 0
while angle < n_angles:
for i in xrange(int(base_points_per_division)):
ra = angle*da + da*math.random()
rr = r*dr + dr*random.random()
x = rr*math.cos(ra)
y = rr*math.sin(ra)
points.append((x,y))
angle += 1
base_points_per_division = base_points_per_division*increase_per_level
ring += 1
я протестировал его с параметрами:
n_rings = 20
n_angles = 20
base_points = .9
increase_per_level = 1.1
и получил следующие результаты:
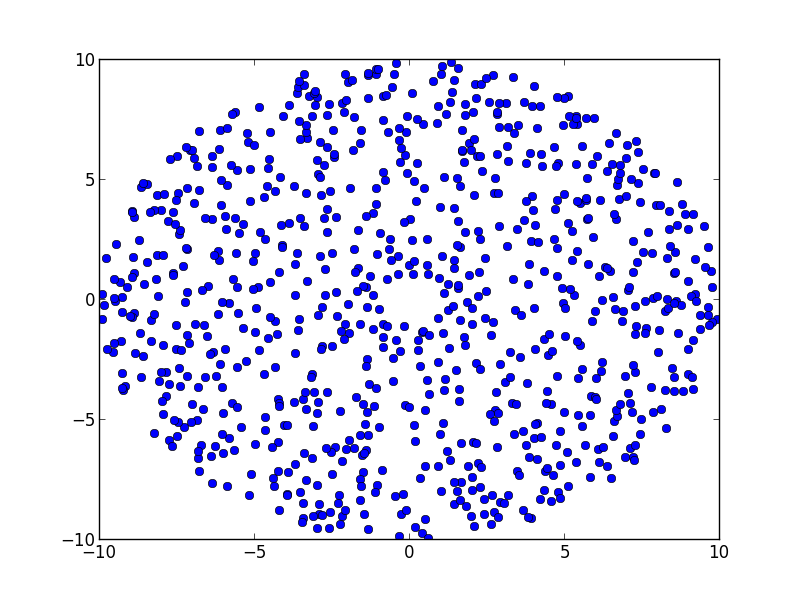
он выглядит более плотным, чем ваше предоставленное изображение, но я полагаю, что дальнейшая настройка этих переменных может быть полезной.
вы можете добавить дополнительную часть для того чтобы масштабировать плотность правильно путем высчитывать число пунктов в кольцо.
points_per_ring = плотностьматематика.Пи(dr* * 2)*(2 * n+1) points_per_division = points_per_ring / n_angles
это обеспечит еще лучшее масштабированное распределение.
density = .03
points = []
ring = 0
while ring < n_rings:
angle = 0
base_points_per_division = density*math.pi*(dr**2)*(2*ring+1)/n_angles
while angle < n_angles:
for i in xrange(int(base_points_per_division)):
ra = angle*da + min(da,da*random.random())
rr = ring*dr + dr*random.random()
x = rr*math.cos(ra)
y = rr*math.sin(ra)
points.append((x,y))
angle += 1
ring += 1
дает лучшие результаты, используя следующие параметры
R = 1.
n_rings = 10.
n_angles = 10.
density = 10/(dr*da) # ~ ten points per unit area
С графиком...
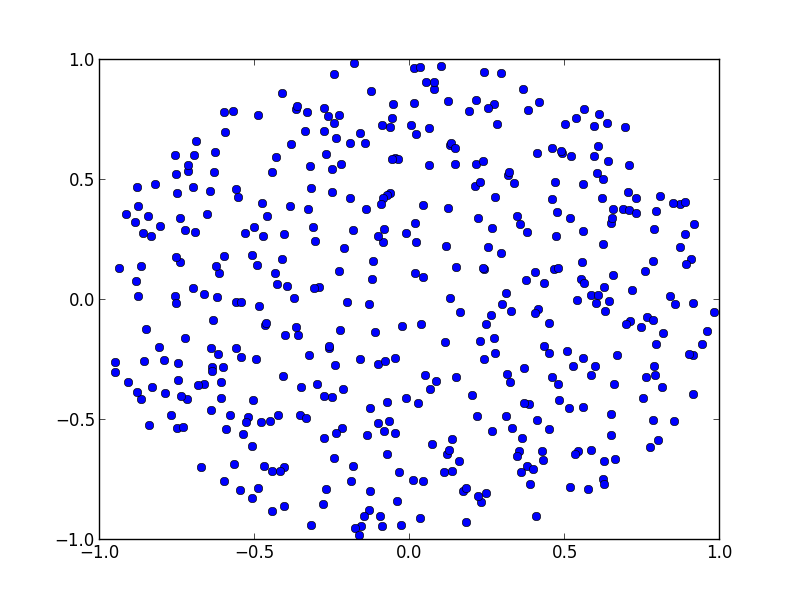
и для удовольствия вы можете изобразить деления, чтобы увидеть, насколько хорошо он соответствует вашему distriubtion и регулировать.
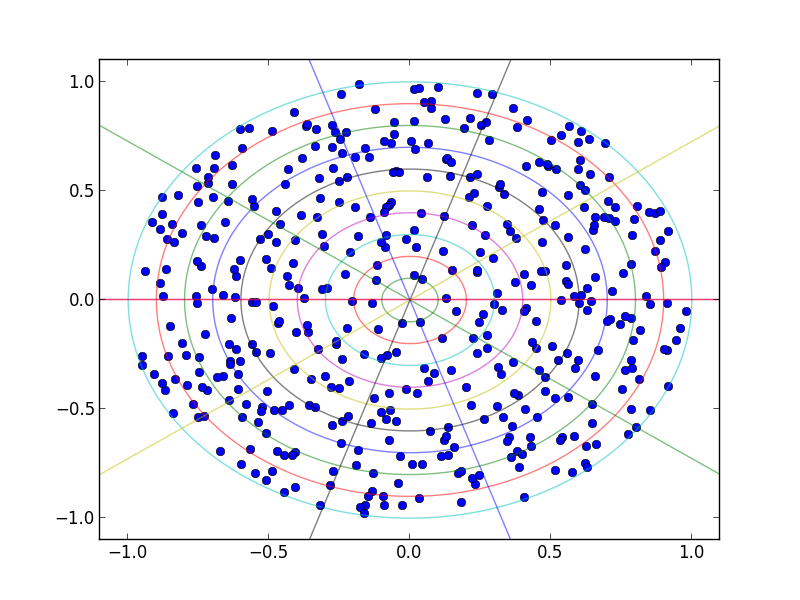
простое решение на основе Выбор Точки Диска от MathWorld:
import numpy as np
import matplotlib.pyplot as plt
n = 1000
r = np.random.uniform(low=0, high=1, size=n) # radius
theta = np.random.uniform(low=0, high=2*np.pi, size=n) # angle
x = np.sqrt(r) * np.cos(theta)
y = np.sqrt(r) * np.sin(theta)
# for plotting circle line:
a = np.linspace(0, 2*np.pi, 500)
cx,cy = np.cos(a), np.sin(a)
fg, ax = plt.subplots(1, 1)
ax.plot(cx, cy,'-', alpha=.5) # draw unit circle line
ax.plot(x, y, '.') # plot random points
ax.axis('equal')
ax.grid(True)
fg.canvas.draw()
plt.show()
дает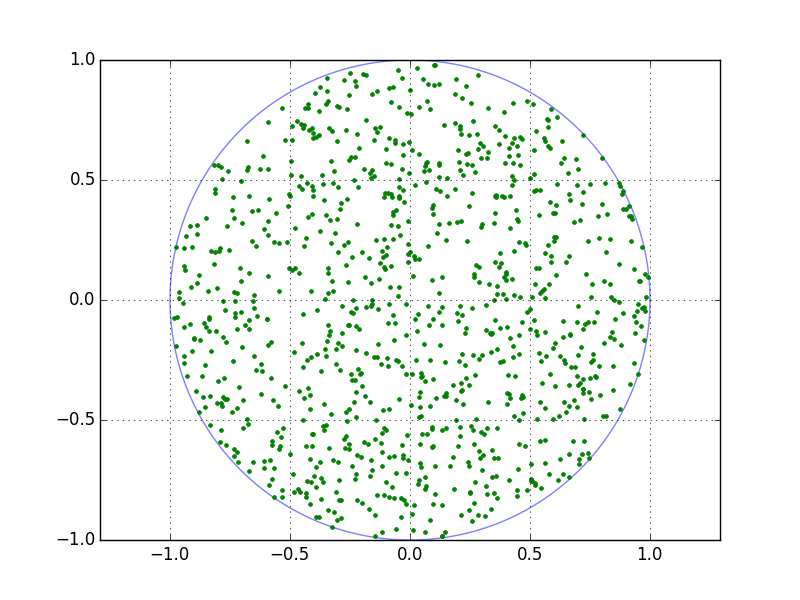 .
.
кроме того, вы также можете создать регулярную сетку и исказить ее случайным образом:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.tri as tri
n = 20
tt = np.linspace(-1, 1, n)
xx, yy = np.meshgrid(tt, tt) # create unit square grid
s_x, s_y = xx.ravel(), yy.ravel()
ii = np.argwhere(s_x**2 + s_y**2 <= 1).ravel() # mask off unwanted points
x, y = s_x[ii], s_y[ii]
triang = tri.Triangulation(x, y) # create triangluar grid
# distort the grid
g = .5 # distortion factor
rx = x + np.random.uniform(low=-g/n, high=g/n, size=x.shape)
ry = y + np.random.uniform(low=-g/n, high=g/n, size=y.shape)
rtri = tri.Triangulation(rx, ry, triang.triangles) # distorted grid
# for circle:
a = np.linspace(0, 2*np.pi, 500)
cx,cy = np.cos(a), np.sin(a)
fg, ax = plt.subplots(1, 1)
ax.plot(cx, cy,'k-', alpha=.2) # circle line
ax.triplot(triang, "g-", alpha=.4)
ax.triplot(rtri, 'b-', alpha=.5)
ax.axis('equal')
ax.grid(True)
fg.canvas.draw()
plt.show()
дает 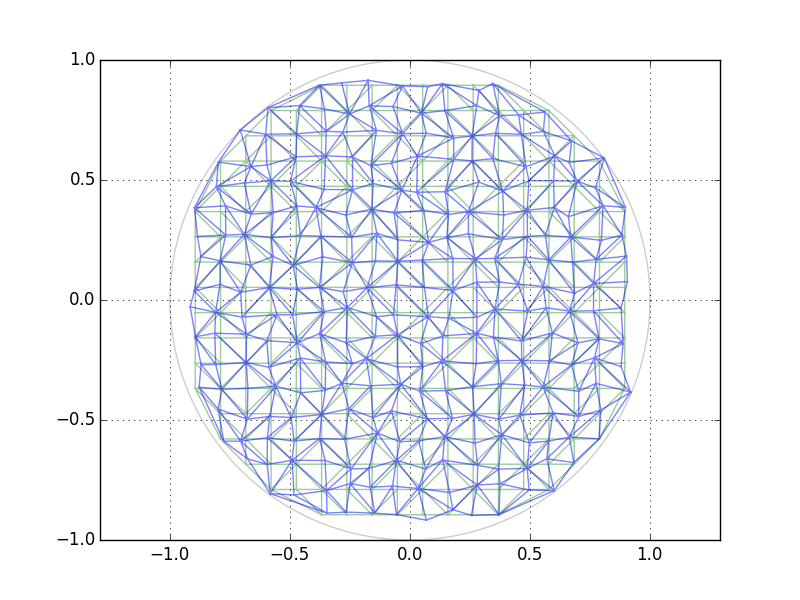
треугольники просто существуют для визуализации. Очевидным недостатком является то, что в зависимости от вашего выбора решетки, либо в центре, либо на границах (как показано здесь), будет больше или менее большие "дыры" из-за дискретизации сетки.
в зависимости от того, насколько случайными должны быть точки, может быть достаточно просто сделать сетку точек внутри диска, а затем переместить каждую точку на некоторую небольшую, но случайную величину.
возможно, вы хотите больше случайности, но если вы просто хотите заполнить свой диск равномерным распределением точек, которые не находятся на очевидной сетке, вы можете попробовать спираль со случайной фазой.
import math
import random
import pylab
n = 300
alpha = math.pi * (3 - math.sqrt(5)) # the "golden angle"
phase = random.random() * 2 * math.pi
points = []
for k in xrange(n):
theta = k * alpha + phase
r = math.sqrt(float(k)/n)
points.append((r * math.cos(theta), r * math.sin(theta)))
pylab.scatter(*zip(*points))
pylab.show()
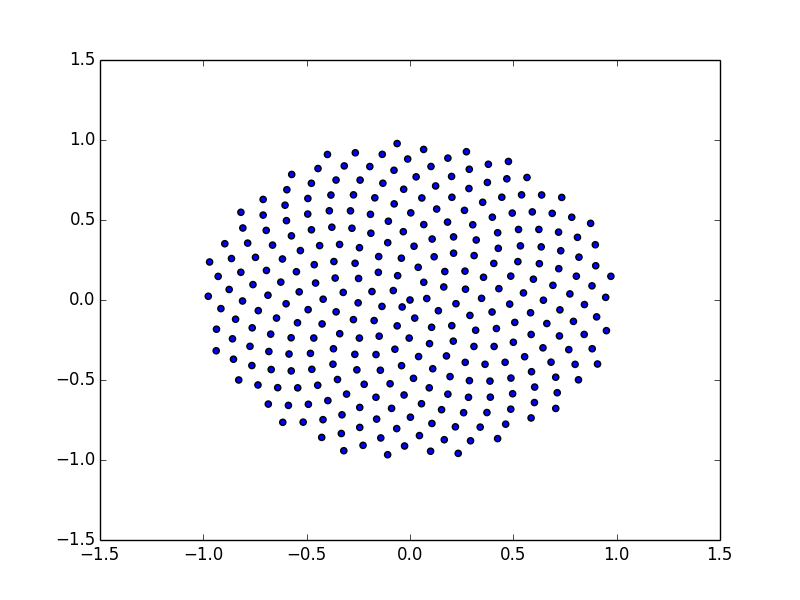
теория вероятностей гарантирует, что метод отбраковки является подходящим методом для создания равномерно распределенных точек внутри диска D (0,r), центрированных в начале координат и радиуса r. А именно, генерируются точки внутри квадрата [- r,r] x [-r, r], пока точка не попадает в диск:
do{
generate P in [-r,r]x[-r,r];
}while(P[0]**2+P[1]**2>r);
return P;
unif_rnd_disk является функцией генератора, реализующей этот метод отклонения:
import matplotlib.pyplot as plt
import numpy as np
import itertools
def unif_rnd_disk(r=1.0):
pt=np.zeros(2)
while True:
yield pt
while True:
pt=-r+2*r*np.random.random(2)
if (pt[0]**2+pt[1]**2<=r):
break
G=unif_rnd_disk()# generator of points in disk D(0,r=1)
X,Y=zip(*[pt for pt in itertools.islice(G, 1, 1000)])
plt.scatter(X, Y, color='r', s=3)
plt.axis('equal')
если мы хотим создать точки на диске с центром в C(a, b), мы должны применить перевод к точкам на диске D (0, r):
C=[2.0, -3.5]
plt.scatter(C[0]+np.array(X), C[1]+np.array(Y), color='r', s=3)
plt.axis('equal')
