Теория пересечений лучей-коробок
Я хочу определить точку пересечения между Лучом и коробкой. Поле определяется его min 3D координатами и max 3D координатами, а Луч определяется его началом и направлением, в котором он указывает.
В настоящее время я формирую плоскость для каждой грани коробки, и я пересекаю луч с плоскостью. Если луч пересекает плоскость, я проверяю, действительно ли точка пересечения находится на поверхности коробки. Если это так, я проверяю, является ли это ближайшее пересечение для этого луча и я возвращаю ближайшее пересечение.
способ, которым я проверяю, находится ли точка пересечения плоскости на самой поверхности коробки, через функцию
bool PointOnBoxFace(R3Point point, R3Point corner1, R3Point corner2)
{
double min_x = min(corner1.X(), corner2.X());
double max_x = max(corner1.X(), corner2.X());
double min_y = min(corner1.Y(), corner2.Y());
double max_y = max(corner1.Y(), corner2.Y());
double min_z = min(corner1.Z(), corner2.Z());
double max_z = max(corner1.Z(), corner2.Z());
if(point.X() >= min_x && point.X() <= max_x &&
point.Y() >= min_y && point.Y() <= max_y &&
point.Z() >= min_z && point.Z() <= max_z)
return true;
return false;
}
здесь corner1 - один угол прямоугольника для этой грани окна и corner2 противоположный угол. Моя реализация работает большую часть времени, но иногда она дает мне неправильное пересечение. Пожалуйста, смотрите изображение:
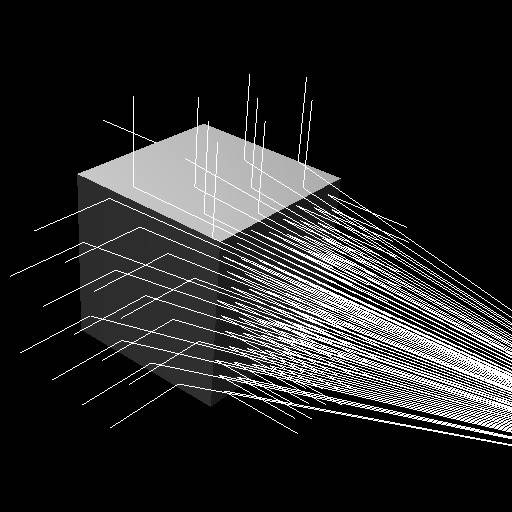
изображение показывает лучи исходящий из глаза камеры и ударяющийся о поверхность коробки. Остальные лучи-нормали к поверхности ящика. Можно видеть, что один луч, в частности (это на самом деле нормальный, который виден), выходит из "задней" части коробки, тогда как нормальный должен подниматься из верхней части коробки. Это кажется странным, так как есть несколько других лучей, которые попадают в верхнюю часть коробки правильно.
мне было интересно, как я проверяю, находится ли точка пересечения на коробке правильно или если я должен использовать какой-то другой алгоритм.
спасибо.
5 ответов
увеличение вещей Эпсилоном на самом деле не является отличным способом сделать это, так как теперь у вас есть граница размера Эпсилона на краю вашего ящика, через который могут проходить лучи. Таким образом, вы избавитесь от этого (относительно распространенного) странного набора ошибок и получите другой (более редкий) набор странных ошибок.
Я предполагаю, что вы уже представляете, что ваш луч движется с некоторой скоростью вдоль своего вектора и находит время пересечения с каждой плоскостью. Так, например, если вы пересечение плоскости на x=x0, и луч идет в направлении (rx,ry,rz) С (0,0,0), тогда время пересечения составляет t = x0/rx. Если t отрицательно, игнорируйте его-вы идете в другую сторону. Если t это ноль, вы должны решить, как обращаться с этим особым случаем-если вы уже находитесь в самолете, вы отскакиваете от него или проходите через него? Вы также можете захотеть обработать rx==0 как особый случай (так что вы можете ударить по краю коробки).
в любом случае, теперь у вас есть точно координаты, по которым вы ударились об эту плоскость: они (t*rx , t*ry , t*rz). Теперь вы можете просто прочитать ли t*ry и t*rz находятся внутри прямоугольника, в котором они должны быть (т. е. между min и max для куба вдоль этих осей). вы не тестируете координату x, потому что вы уже знаете, что попали в нее опять же, вы должны решить, следует ли / как обрабатывать углы удара в качестве особого случая. Кроме того, теперь вы можете заказать столкновений с различными поверхностями по времени и выбрать первый как точка столкновения.
это позволяет вычислять, не прибегая к произвольным Эпсилон-факторам, пересекает ли и где ваш луч ваш куб, с точностью, возможной с арифметикой с плавающей запятой.
таким образом, вам просто нужно три функции, как тот, который у вас уже есть: один для тестирования, попали ли вы в yz предполагая, что вы попали x, и соответствующие для xz и xy предполагая, что вы попали y и z соответственно.
Edit: код добавлен (дословно) показать, как делать тесты по-разному для каждой оси:
#define X_FACE 0
#define Y_FACE 1
#define Z_FACE 2
#define MAX_FACE 4
// true if we hit a box face, false otherwise
bool hit_face(double uhit,double vhit,
double umin,double umax,double vmin,double vmax)
{
return (umin <= uhit && uhit <= umax && vmin <= vhit && vhit <= vmax);
}
// 0.0 if we missed, the time of impact otherwise
double hit_box(double rx,double ry, double rz,
double min_x,double min_y,double min_z,
double max_x,double max_y,double max_z)
{
double times[6];
bool hits[6];
int faces[6];
double t;
if (rx==0) { times[0] = times[1] = 0.0; }
else {
t = min_x/rx;
times[0] = t; faces[0] = X_FACE;
hits[0] = hit_box(t*ry , t*rz , min_y , max_y , min_z , max_z);
t = max_x/rx;
times[1] = t; faces[1] = X_FACE + MAX_FACE;
hits[1] = hit_box(t*ry , t*rz , min_y , max_y , min_z , max_z);
}
if (ry==0) { times[2] = times[3] = 0.0; }
else {
t = min_y/ry;
times[2] = t; faces[2] = Y_FACE;
hits[2] = hit_box(t*rx , t*rz , min_x , max_x , min_z , max_z);
t = max_y/ry;
times[3] = t; faces[3] = Y_FACE + MAX_FACE;
hits[3] = hit_box(t*rx , t*rz , min_x , max_x , min_z , max_z);
}
if (rz==0) { times[4] = times[5] = 0.0; }
else {
t = min_z/rz;
times[4] = t; faces[4] = Z_FACE;
hits[4] = hit_box(t*rx , t*ry , min_x , max_x , min_y , max_y);
t = max_z/rz;
times[5] = t; faces[5] = Z_FACE + MAX_FACE;
hits[5] = hit_box(t*rx , t*ry , min_x , max_x , min_y , max_y);
}
int first = 6;
t = 0.0;
for (int i=0 ; i<6 ; i++) {
if (times[i] > 0.0 && (times[i]<t || t==0.0)) {
first = i;
t = times[i];
}
}
if (first>5) return 0.0; // Found nothing
else return times[first]; // Probably want hits[first] and faces[first] also....
}
(Я только что набрал это, не компилировал его, поэтому остерегайтесь ошибок.)
(Edit: просто исправлено i ->first.)
в любом случае, дело в том, что вы рассматриваете три направления отдельно и проверяете, произошло ли столкновение в правом поле в координатах (u,v), где (u, v) либо (x, y), (x, z), либо (y, z) в зависимости от того, какой самолет вы попали.
PointOnBoxFace должна быть двухмерная проверка вместо трехмерной. Например, если вы тестируете против z = z_min plane, тогда вам нужно только сравнить x и y в соответствующих границах. Вы уже поняли, что z координаты верны. Точность с плавающей запятой, вероятно, спотыкается, когда вы "перепроверяете" третью координату.
z_min это 1.0, вы первый тест против этой плоскости. Вы находите точка пересечения (x, y, 0.999999999). Теперь, хотя x и y в пределах z не совсем верно.может быть, этот луч в конечном итоге проходит точно через край коробки? Ошибки округления с плавающей запятой могут привести к тому, что он будет пропущен как правой, так и задней гранью.
EDIT: игнорировать этот ответ (см. комментарии ниже, где мне довольно убедительно показана ошибка моих способов).
вы проверяете, находится ли точка внутри тома, но точка находится на периферии этого тома, поэтому вы можете обнаружить, что это "бесконечно малое" расстояние вне Тома. Попробуйте вырастить коробку с помощью небольшого Эпсилона, например:
double epsilon = 1e-10; // Depends the scale of things in your code.
double min_x = min(corner1.X(), corner2.X()) - epsilon;
double max_x = max(corner1.X(), corner2.X()) + epsilon;
double min_y = min(corner1.Y(), corner2.Y()) - epsilon;
...
технически правильным способом сравнения почти равных чисел является приведение их битовых представлений к ints и сравните целые числа для некоторого небольшого смещения, например, в C:
#define EPSILON 10 /* some small int; tune to suit */
int almostequal(double a, double b) {
return llabs(*(long long*)&a - *(long long*)&b) < EPSILON;
}
конечно, это не так просто в C#, но, возможно, небезопасная семантика может достичь того же эффекта. (Спасибо @Novox за его комментарии, которые приводят меня к хорошему страница объясняя эту технику подробно.)
