Точка внутри правильного шестиугольника

если вы уменьшите проблему до проверки {x = 0, y = 0, d = 1} в одном квадранте вы можете сделать очень просто.

public boolean IsInsideHexagon(float x0, float y0, float d, float x, float y) {
    float dx = Math.abs(x - x0)/d;
    float dy = Math.abs(y - y0)/d;
    float a = 0.25 * Math.sqrt(3.0);
    return (dy <= a) && (a*dx + 0.25*dy <= 0.5*a);
}

• dy <= a проверяет, что точка находится ниже горизонтального края.
• a*dx + 0.25*dy <= 0.5*a проверяет, что точка находится слева от наклонной правого края.

на {x0 = 0, y0 = 0, d = 1}, угловые точки будут (±0.25, ±0.43) и (±0.5, 0.0).

это то, что я использовал:

public bool InsideHexagon(float x, float y)
{
    // Check length (squared) against inner and outer radius
    float l2 = x * x + y * y;
    if (l2 > 1.0f) return false;
    if (l2 < 0.75f) return true; // (sqrt(3)/2)^2 = 3/4

    // Check against borders
    float px = x * 1.15470053838f; // 2/sqrt(3)
    if (px > 1.0f || px < -1.0f) return false;

    float py = 0.5f * px + y;
    if (py > 1.0f || py < -1.0f) return false;

    if (px - py > 1.0f || px - py < -1.0f) return false;

    return true;
}

px и py координаты x и y проецируется на систему координат, где гораздо проще проверить границы.

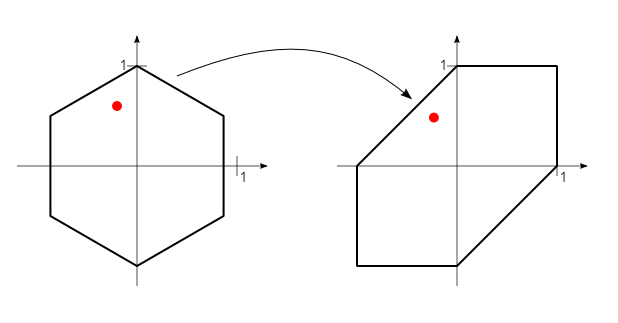
Похоже, вы знаете общее решение: "кажется, это излишне использовать...". Так вот моя идея:

вычислить расстояние от точки до центра и назовем его l.

тогда вы можете сравнить его с inradius (r) и circumradius (R). если l < r затем точка находится внутри шестиугольника, если l > R затем снаружи. Если r < l < R затем вы должны проверить против каждой стороны соответственно, но так как R - r очень мало (13% длины стороны шестигранника), поэтому вероятность что вам придется делать сложные расчеты крошечный.

формулы можно найти здесь:http://mathworld.wolfram.com/Hexagon.html

сначала я бы проверил, находится ли точка внутри вписанного круга (вы можете легко вычислить радиус вписанного круга) или вне описанного круга (который у вас уже есть).

первое означает, что точка находится внутри, последнее означает, что она вне.

статистически, большинство входных точек должны позволить вам принять решение на основе вышеуказанных простых тестов.

для наихудшего сценария (точка находится между вписанными и описанными кругами), я думаю вы можете найти две вершины, которые ближе всего к точке, а затем посмотреть, на какой стороне сегмента V1V2 находится точка (внутренняя или внешняя, относительно центра O). Частный случай: точка равна одной из вершин => она находится внутри.

Если у меня будет более умная идея (или если я когда-нибудь начну действительно изучать тригонометрию), я отредактирую ответ, чтобы сообщить вам :)

вычесть положение центра шестиугольника из вашей точки P, чтобы получить вектор V. Затем возьмите точечное произведение V со следующими векторами, которые соответствуют трем парам противоположных ребер шестиугольника:

[0,1] ; the edges that are flat with the horizontal
[cos(30),sin(30)] ; the upper-right and lower-left edges
[cos(-30),sin(-30)] ; the lower-right and upper-left edges

Если любое из точечных произведений больше по величине, чем расстояние от центра шестиугольника до одного из его краев, то точка не находится внутри шестиугольника.

для справки, точечное произведение векторов [a, b] и [c, d] равно a * c+b * d.

угол "30" выше в градусах ;)

что вы хотите, чтобы код, чтобы выяснить, находится ли точка внутри выпуклого многоугольника, шестиугольник является частным случаем этого.

вот хороший ответ: https://stackoverflow.com/a/34689268/516188

Я изменил эту функцию для своего использования, я нахожу свою версию более ясной. Это typescript (вы просто косите, и это javascript):

function vectorX(v: Vector): number {
    return v[1].x - v[0].x;
}

function vectorY(v: Vector): number {
    return v[1].y - v[0].y;
}

function crossProduct(v1: Vector, v2: Vector): number {
    return vectorX(v1)*vectorY(v2) - vectorY(v1)*vectorX(v2);
}

function isInConvexPolygon(testPoint: Point, polygon: Polygon): boolean {
    // https://stackoverflow.com/a/34689268/516188
    if (polygon.length < 3) {
        throw "Only supporting polygons of length at least 3";
    }
    // going through all the edges around the polygon. compute the
    // vector cross-product http://allenchou.net/2013/07/cross-product-of-2d-vectors/
    // to find out for each edge on which side of the edge is the point.
    // if the point is on the same side for all the edges, it's inside
    let initCrossIsPositive = undefined;
    for (var i=0;i<polygon.length;i++) {
        if (polygon[i].x === testPoint.x &&
            polygon[i].y === testPoint.y) {
            // testPoint is an edge of the polygon
            return true;
        }
        const curPointOnEdge = polygon[i];
        const nextPointOnEdge = polygon[(i+1)%polygon.length];
        const vector1 = <[Point,Point]>[curPointOnEdge, nextPointOnEdge];
        const vector2 = <[Point,Point]>[curPointOnEdge, testPoint];
        const cross = crossProduct(vector1, vector2);
        if (initCrossIsPositive === undefined) {
            initCrossIsPositive = cross > 0;
        } else {
            if (initCrossIsPositive !== (cross > 0)) {
                return false;
            }
        }
    }
    // all the cross-products have the same sign: we're inside
    return true;
}