учитывая график, чтобы определить, является ли он деревом или нет в направленных и неориентированных графах?

Я хотел бы знать быстрый алгоритм, чтобы определить, является ли данный граф деревом или нет. этой post, похоже, имеет дело с этим, но не очень ясно. По этому, если граф ациклический, то это дерево. если вы рассмотрите примеры направленного и неориентированного графа, на мой взгляд, только 1 и 4 являются деревом, но 3 не является ни циклическим, ни деревом, я полагаю.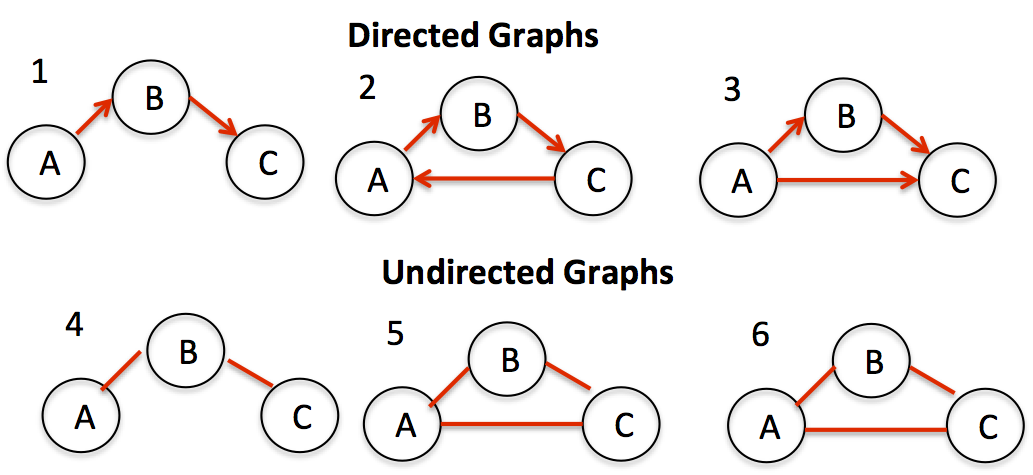enter image description here

Итак, мой вопрос: что нужно проверить, чтобы увидеть, является ли график деревом или нет для обоих направленный и неориентированный граф эффективным образом?

делая один шаг вперед, чтобы увидеть, если существует дерево-это двоичное дерево или нет?

10
algorithm cyclic graph tree

1 ответов

для ориентированного графа:

  • найти вершину только с исходящими ребрами (если таких вершин больше одной или нет, не удается).

  • сделайте BFS или DFS из этой вершины. Если вы столкнулись с уже посещенной вершиной, это не дерево.

  • Если вы закончили и есть неисследованные вершины, это не дерево - граф не связан.

  • в противном случае, это дерево.

  • чтобы проверить наличие двоичного дерева, дополнительно проверьте, имеет ли каждая вершина не более 2 исходящих ребер.

для неориентированного графа:

  • Проверьте цикл с простым поиском глубины (начиная с любой вершины) - " если неисследованное ребро ведет к узлу, посещенному ранее, то график содержит цикл." если есть цикл, это не дерево.

  • Если выше процесс оставляет некоторые вершины неисследованными, это не дерево, потому что оно не связано.

  • в противном случае, это дерево.

  • чтобы проверить наличие двоичного дерева, дополнительно проверьте, что все вершины имеют 1-3 ребра (один для родителя и 2 для детей).

    проверка корня, т. е. содержит ли одна вершина 1-2 ребра, не нужна, так как там до быть вершинами с 1-2 ребрами в ациклическом Связном неориентированном диаграмма.

    обратите внимание, что идентификация корня в общем случае невозможна (это может быть возможно в особых случаях), поскольку во многих неориентированных графах более одного узла можно сделать корнем, если мы сделаем его двоичным деревом.

15