Умножение тензора с tensordot и NumPy

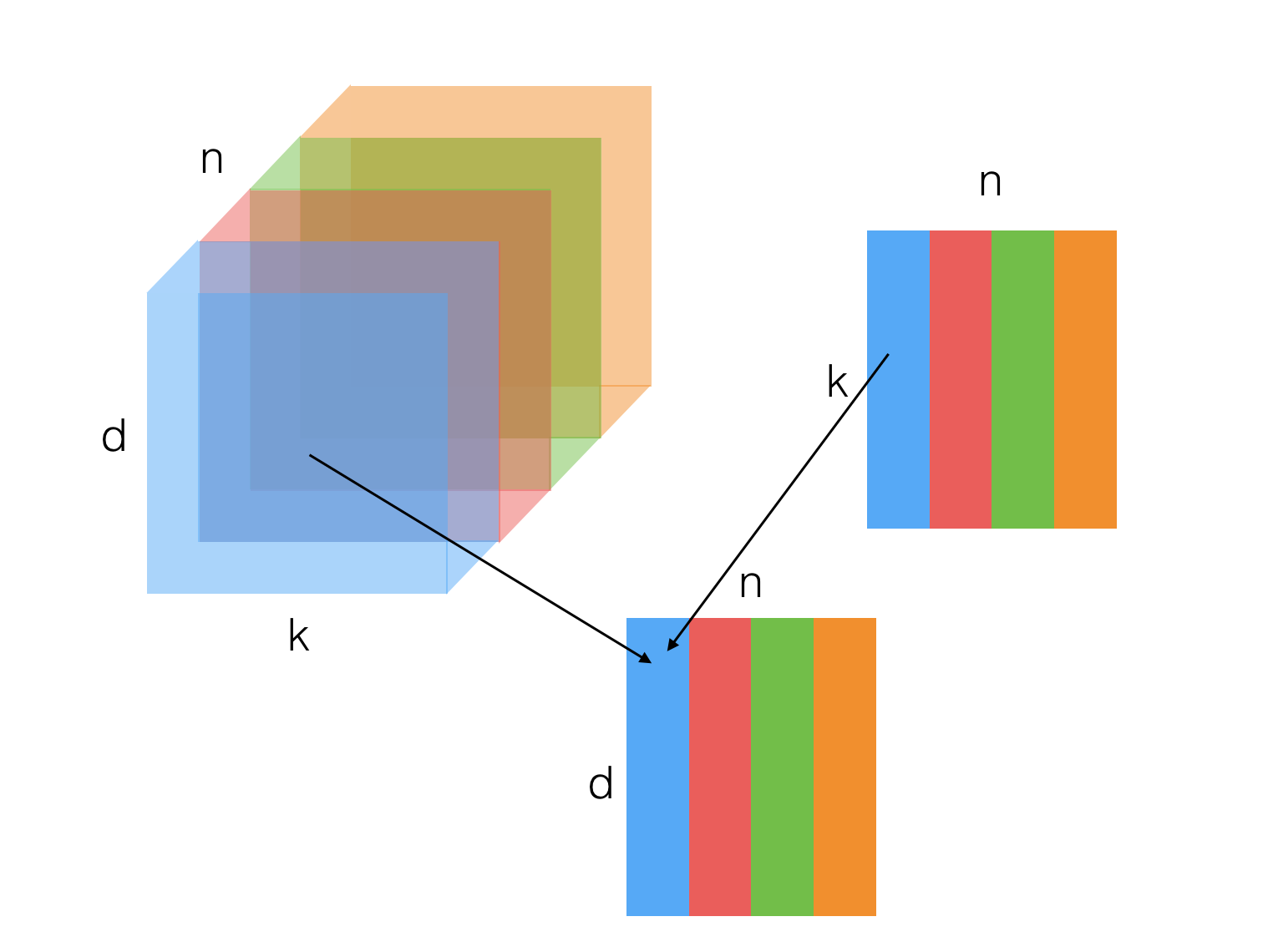
у меня есть тензор U, состоящий из n матриц размерности (d,k) и матрицы V размерности (k,n).

Я хотел бы умножить их так,чтобы результат возвращал матрицу размерности (d, n), в которой столбец j является результатом умножения матрицы между матрицей j из U и столбцом j из V.

enter image description here

один из возможных способов получить это:

for j in range(n):
    res[:,j] = U[:,:,j] * V[:,j]

мне интересно, есть ли более быстрый подход с использованием numpy библиотека. В частности, я думаю о np.tensordot().

этот небольшой фрагмент позволяет мне умножить одну матрицу на скаляр, но очевидное обобщение на вектор не возвращает того, на что я надеялся.

a = np.array(range(1, 17))
a.shape = (4,4)
b = np.array((1,2,3,4,5,6,7))
r1 = np.tensordot(b,a, axes=0)

какие будут предложения?

8
linear-algebra matrix numpy performance python

1 ответов

есть несколько способов сделать это. Первое, что приходит на ум, это np.einsum:

# some fake data
gen = np.random.RandomState(0)
ni, nj, nk = 10, 20, 100
U = gen.randn(ni, nj, nk)
V = gen.randn(nj, nk)

res1 = np.zeros((ni, nk))
for k in range(nk):
    res1[:,k] = U[:,:,k].dot(V[:,k])

res2 = np.einsum('ijk,jk->ik', U, V)

print(np.allclose(res1, res2))
# True

np.einsum использует нотация Эйнштейна выразить тензор схватки. В выражении 'ijk,jk->ik' выше i,j и k - это индексы, соответствующие различным измерениям U и V. Каждая группировка, разделенная запятыми, соответствует одному из операндов, переданных в np.einsum (в данном случае U есть размеры ijk и V имеет размеры jk). The '->ik' part задает размеры выходного массива. Любые измерения с индексами, отсутствующими в выходной строке, суммируются.

np.einsum невероятно полезно для выполнения сложных тензорных сокращений, но может потребоваться некоторое время, чтобы полностью обернуть голову вокруг того, как это работает. Вы должны взглянуть на примеры в документации (ссылка выше).

некоторые другие опции:

  1. умножение по элементам с вещания, с последующим суммированием:

    res3 = (U * V[None, ...]).sum(1)

  2. inner1d С нагрузкой транспонирование:

    from numpy.core.umath_tests import inner1d

res4 = inner1d(U.transpose(0, 2, 1), V.T)

некоторые ориентиры:

In [1]: ni, nj, nk = 100, 200, 1000

In [2]: %%timeit U = gen.randn(ni, nj, nk); V = gen.randn(nj, nk)
   ....: np.einsum('ijk,jk->ik', U, V)
   ....: 
10 loops, best of 3: 23.4 ms per loop

In [3]: %%timeit U = gen.randn(ni, nj, nk); V = gen.randn(nj, nk)
(U * V[None, ...]).sum(1)
   ....: 
10 loops, best of 3: 59.7 ms per loop

In [4]: %%timeit U = gen.randn(ni, nj, nk); V = gen.randn(nj, nk)
inner1d(U.transpose(0, 2, 1), V.T)
   ....: 
10 loops, best of 3: 45.9 ms per loop
7