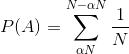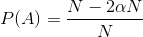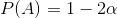Вероятность на основе разбиения quicksort
я столкнулся с этим вопросом:
пусть 0
Its answer is 1-2*α.
кто-нибудь может объяснить мне как это ответ пришел?пожалуйста помочь.
5 ответов
выбор оси элемента является случайным с равномерным распределением.
в массиве есть N элементов, и мы предположим, что N является большим (или мы не получим ответ, который мы хотим).
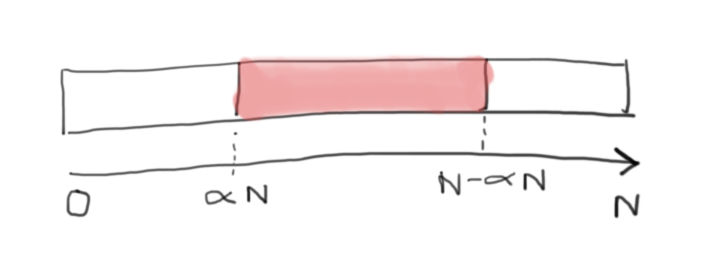
Если 0≤α≤1, то вероятность того, что число элементов меньше оси, меньше, чем aN, равна α. Вероятность того, что количество элементов больше чем ось меньше, чем aN то же самое. Если α≤ 1/2, то эти две возможности эксклюзивный.
сказать, что меньший подмассив имеет длину ≥aN, означает сказать, что ни одно из этих условий не выполняется, поэтому вероятность равна 1-2α.
длина массива равна n. Для меньшей длины массива >= pivot должен быть больше, чем количество элементов. В то же время pivot должен быть меньше, чем количество элементов( иначе меньший размер массива будет меньше требуемого)
Итак, из n элементов мы должны выбрать один из (n-2α)n элементов.
искомая вероятность равна n(1-2α)/Н.
следовательно, 1-2α
еще один подход к решению проблемы (для тех, у кого непросто понять, как у меня).
первый. Так как речь идет о "меньшем из двух подмассивов", то его длина меньше 1/2 * n (n - количество элементов в исходном массиве).
второй. Если 0
третье. Давайте представим себе кости с числами от 1 до 6 на его сторонах. Позволяет выбрать число от 1 до 6, например 4. Теперь бросай кости. Каждое число имеет вероятность 1/6 быть результатом этого броска. Таким образом, для события "результат меньше или равен 4" мы имеем вероятность, равную сумме вероятностей каждого из этих результатов. И у нас есть числа 1, 2, 3 и 4. Всего p (x 4) = 1-p(x
В-четвертых. Вернемся к нашей проблеме. "Выбранное число" теперь a * n. И мы будем бросать кости с числами от 0 до (1/2 * n), чтобы получить k - количество элементов в наименьшем из подмножеств. Вероятность того, что исход ограничен (a * n) в наибольшей степени равна сумме вероятностей всех исходов от 0 до (a * n). И вероятность для любого конкретного результат k равен p (k) = 1 / (1/2 * n).
поэтому p (k
из этого можно легко заключить, что p (k > a * n) = 1 - p(k
вероятность будет, количество желаемых элементов / общее количество элементов. В этом случае ((1-an) - (an))/n Поскольку α лежит между 0 и 0.5, (1-α) должно быть больше α.Следовательно, число элементов, содержащихся между ними, будет, (1-α-α)n=(1-2α)n и так, вероятность была бы, (1-2α)n/n=1-2α
другие ответы не совсем щелкнули со мной, так что вот еще один дубль:
Если хотя бы один из 2 подмассивов должны быть 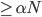
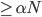
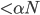
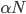
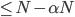
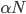
этот значит, что 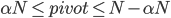
то, что мы хотим вычислить, - это вероятность этого события (назовем его A) i.e 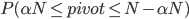
способ вычисления вероятности события заключается в суммировании вероятности составляющих результатов, т. е. что ось приземляется на 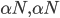
эта сумма выражается так:
что легко упрощает кому:
с некоторой отменой мы получаем: