Выбор рулетки в генетических алгоритмах
может ли кто-нибудь предоставить псевдо-код для функции выбора рулетки? Как бы я это реализовал:
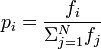
Я не очень понимаю как читать эту математическую нотацию. Я никогда не брал никакой вероятности или статистики.
12 ответов
прошло несколько лет с тех пор как я сделал это сам, однако следующие псевдо-код был найден достаточно легко в гугле.
for all members of population
sum += fitness of this individual
end for
for all members of population
probability = sum of probabilities + (fitness / sum)
sum of probabilities += probability
end for
loop until new population is full
do this twice
number = Random between 0 and 1
for all members of population
if number > probability but less than next probability
then you have been selected
end for
end
create offspring
end loop
сайт, откуда это можно найти здесь если вам нужна дополнительная информация.
уже много правильных решений, но я думаю, что этот код яснее.
def select(fs):
p = random.uniform(0, sum(fs))
for i, f in enumerate(fs):
if p <= 0:
break
p -= f
return i
кроме того, если вы накапливаете fs, вы можете создать более эффективное решение.
cfs = [sum(fs[:i+1]) for i in xrange(len(fs))]
def select(cfs):
return bisect.bisect_left(cfs, random.uniform(0, cfs[-1]))
это и быстрее, и это чрезвычайно сжатый код. STL в C++ имеет аналогичный алгоритм разделения, доступный, если это язык, который вы используете.
опубликованный псевдокод содержал некоторые неясные элементы, и это добавляет сложность генерации потомство вместо выполнения чистого отбора. Вот простая реализация python этого псевдокода:
def roulette_select(population, fitnesses, num):
""" Roulette selection, implemented according to:
<http://stackoverflow.com/questions/177271/roulette
-selection-in-genetic-algorithms/177278#177278>
"""
total_fitness = float(sum(fitnesses))
rel_fitness = [f/total_fitness for f in fitnesses]
# Generate probability intervals for each individual
probs = [sum(rel_fitness[:i+1]) for i in range(len(rel_fitness))]
# Draw new population
new_population = []
for n in xrange(num):
r = rand()
for (i, individual) in enumerate(population):
if r <= probs[i]:
new_population.append(individual)
break
return new_population
это называется выбором колеса рулетки через стохастическое принятие:
/// \param[in] f_max maximum fitness of the population
///
/// \return index of the selected individual
///
/// \note Assuming positive fitness. Greater is better.
unsigned rw_selection(double f_max)
{
for (;;)
{
// Select randomly one of the individuals
unsigned i(random_individual());
// The selection is accepted with probability fitness(i) / f_max
if (uniform_random_01() < fitness(i) / f_max)
return i;
}
}
среднее количество попыток, необходимых для одного выбора:
τ = fМакс / avg (f)
- fМакс это максимальная пригодность населения
- avg (f) - средняя пригодность
τ явно не зависит от количества особей в популяции (N) , но соотношение может меняться с Н.
однако во многих приложениях (где пригодность остается ограниченной и средняя пригодность не уменьшается до 0 для увеличения N) τ не увеличивается неограниченно с N и, следовательно,типичной сложностью этого алгоритма является O (1) (выбор колеса рулетки с помощью алгоритмов поиска имеет сложность O(N) или O(log N)).
распределение вероятностей этой процедуры действительно такое же, как и в классической рулетке.
для более подробную информацию см.:
- выбор колеса рулетки через стохастическое принятие (Адам Liposki, Дорота Lipowska - 2011)
вот некоторый код в C:
// Find the sum of fitnesses. The function fitness(i) should
//return the fitness value for member i**
float sumFitness = 0.0f;
for (int i=0; i < nmembers; i++)
sumFitness += fitness(i);
// Get a floating point number in the interval 0.0 ... sumFitness**
float randomNumber = (float(rand() % 10000) / 9999.0f) * sumFitness;
// Translate this number to the corresponding member**
int memberID=0;
float partialSum=0.0f;
while (randomNumber > partialSum)
{
partialSum += fitness(memberID);
memberID++;
}
**// We have just found the member of the population using the roulette algorithm**
**// It is stored in the "memberID" variable**
**// Repeat this procedure as many times to find random members of the population**
приведу пример:
случайный (сумма):: случайный(12) Повторяя через население, мы проверяем следующее: random
давайте выберем 7 в качестве случайного числа.
Index | Fitness | Sum | 7 < Sum
0 | 2 | 2 | false
1 | 3 | 5 | false
2 | 1 | 6 | false
3 | 4 | 10 | true
4 | 2 | 12 | ...
в этом примере наиболее подходящий (индекс 3) имеет самый высокий процент выбора (33%); поскольку случайное число должно приземлиться только в пределах 6 - >10, и это будет выбранный.
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
}
double rand = (((double)rand() / (double)RAND_MAX) * sum);
sum = 0;
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
if (rand < sum) {
//breed i
break;
}
}
профессор Thrun из Стэнфордской лаборатории AI также представил быстрый (er?) повторная выборка кода в python во время его CS373 Udacity. Результат поиска Google привел к следующей ссылке:
http://www.udacity-forums.com/cs373/questions/20194/fast-resampling-algorithm
надеюсь, что это помогает
вот компактная реализация java, которую я недавно написал для выбора рулетки, надеюсь, использовать.
public static gene rouletteSelection()
{
float totalScore = 0;
float runningScore = 0;
for (gene g : genes)
{
totalScore += g.score;
}
float rnd = (float) (Math.random() * totalScore);
for (gene g : genes)
{
if ( rnd>=runningScore &&
rnd<=runningScore+g.score)
{
return g;
}
runningScore+=g.score;
}
return null;
}
выбор колеса рулетки в MatLab:
TotalFitness=sum(Fitness);
ProbSelection=zeros(PopLength,1);
CumProb=zeros(PopLength,1);
for i=1:PopLength
ProbSelection(i)=Fitness(i)/TotalFitness;
if i==1
CumProb(i)=ProbSelection(i);
else
CumProb(i)=CumProb(i-1)+ProbSelection(i);
end
end
SelectInd=rand(PopLength,1);
for i=1:PopLength
flag=0;
for j=1:PopLength
if(CumProb(j)<SelectInd(i) && CumProb(j+1)>=SelectInd(i))
SelectedPop(i,1:IndLength)=CurrentPop(j+1,1:IndLength);
flag=1;
break;
end
end
if(flag==0)
SelectedPop(i,1:IndLength)=CurrentPop(1,1:IndLength);
end
end
Based on my research ,Here is another implementation in C# if there is a need for it:
//those with higher fitness get selected wit a large probability
//return-->individuals with highest fitness
private int RouletteSelection()
{
double randomFitness = m_random.NextDouble() * m_totalFitness;
int idx = -1;
int mid;
int first = 0;
int last = m_populationSize -1;
mid = (last - first)/2;
// ArrayList's BinarySearch is for exact values only
// so do this by hand.
while (idx == -1 && first <= last)
{
if (randomFitness < (double)m_fitnessTable[mid])
{
last = mid;
}
else if (randomFitness > (double)m_fitnessTable[mid])
{
first = mid;
}
mid = (first + last)/2;
// lies between i and i+1
if ((last - first) == 1)
idx = last;
}
return idx;
}
Итак, существует 2 способа выбор колеса рулетки реализация: обычно и Стохастические Принятии один.
обычно:
# there will be some amount of repeating organisms here.
mating_pool = []
all_organisms_in_population.each do |organism|
organism.fitness.times { mating_pool.push(organism) }
end
# [very_fit_organism, very_fit_organism, very_fit_organism, not_so_fit_organism]
return mating_pool.sample #=> random, likely fit, parent!
Стохастические Принятии:
max_fitness_in_population = all_organisms_in_population.sort_by(:fitness)[0]
loop do
random_parent = all_organisms_in_population.sample
probability = random_parent.fitness/max_fitness_in_population * 100
# if random_parent's fitness is 90%,
# it's very likely that rand(100) is smaller than it.
if rand(100) < probability
return random_parent #=> random, likely fit, parent!
else
next #=> or let's keep on searching for one.
end
end
вы можете выбрать либо, они будут возвращать одинаковые результаты.
полезное ресурсы:
http://natureofcode.com/book/chapter-9-the-evolution-of-code - дружественная для начинающих и ясная глава о генетических алгоритмах. объясняет выбор колеса рулетки как ведро деревянных букв (чем больше, как вы положили в-большой шанс выбрать A,обычно).
https://en.wikipedia.org/wiki/Fitness_proportionate_selection - описывает стохастические Принятие.
Я написал версию на C# и действительно ищу подтверждение того, что это действительно правильно:
(roulette_selector-случайное число, которое будет находиться в диапазоне от 0.0 до 1.0)
private Individual Select_Roulette(double sum_fitness)
{
Individual ret = new Individual();
bool loop = true;
while (loop)
{
//this will give us a double within the range 0.0 to total fitness
double slice = roulette_selector.NextDouble() * sum_fitness;
double curFitness = 0.0;
foreach (Individual ind in _generation)
{
curFitness += ind.Fitness;
if (curFitness >= slice)
{
loop = false;
ret = ind;
break;
}
}
}
return ret;
}
