Выборки равномерно распределенных случайных точек внутри сферического объема

Я ищу возможность генерировать случайную однородную выборку местоположений частиц, которые попадают в сферический объем.

изображение ниже (любезно предоставлено http://nojhan.free.fr/metah/) показывает, что я ищу. Это срез через сферу, показывающий равномерное распределение точек:

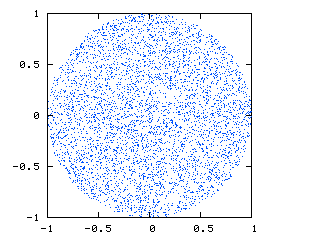
Uniformly distributed circle

это то, что я сейчас получаю:

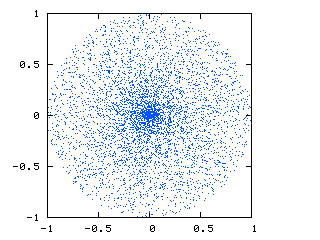
Uniformly Distributed but Cluster Of Points

Вы можете видеть, что есть скопление точки в центре за счет преобразования между сферическими и Декартовыми координатами.

код, который я использую:

def new_positions_spherical_coordinates(self):
   radius = numpy.random.uniform(0.0,1.0, (self.number_of_particles,1)) 
   theta = numpy.random.uniform(0.,1.,(self.number_of_particles,1))*pi
   phi = numpy.arccos(1-2*numpy.random.uniform(0.0,1.,(self.number_of_particles,1)))
   x = radius * numpy.sin( theta ) * numpy.cos( phi )
   y = radius * numpy.sin( theta ) * numpy.sin( phi )
   z = radius * numpy.cos( theta )
   return (x,y,z)

Ниже приведен некоторый код MATLAB, который предположительно создает однородный сферический образец, который похож на уравнение, заданное http://nojhan.free.fr/metah. Я просто не могу расшифровать это или понять, что они сделали. 

function X = randsphere(m,n,r)

% This function returns an m by n array, X, in which 
% each of the m rows has the n Cartesian coordinates 
% of a random point uniformly-distributed over the 
% interior of an n-dimensional hypersphere with 
% radius r and center at the origin.  The function 
% 'randn' is initially used to generate m sets of n 
% random variables with independent multivariate 
% normal distribution, with mean 0 and variance 1.
% Then the incomplete gamma function, 'gammainc', 
% is used to map these points radially to fit in the 
% hypersphere of finite radius r with a uniform % spatial distribution.
% Roger Stafford - 12/23/05

X = randn(m,n);
s2 = sum(X.^2,2);
X = X.*repmat(r*(gammainc(s2/2,n/2).^(1/n))./sqrt(s2),1,n);

Я был бы очень признателен за любые предложения по созданию действительно однородного образца из сферический объем в Python.

Кажется, есть много примеров, показывающих, как пробовать из однородной сферической оболочки, но это, кажется, проще. Проблема связана с масштабированием-должно быть меньше частиц с радиусом 0,1, чем с радиусом 1,0, чтобы генерировать однородный образец из объема сферы.

Edit: исправлено и удалено то, что я просил нормально, и я имел в виду униформу.

30
geometry matlab python random-sample uniform-distribution

8 ответов

в то время как я предпочитаю метод отбрасывания для сфер, для полноты Я предлагаю точное решение.

в сферических координатах, используяправила отбора проб:

phi = random(0,2pi)
costheta = random(-1,1)
u = random(0,1)

theta = arccos( costheta )
r = R * cuberoot( u )

теперь у вас есть (r, theta, phi) группы, которая может быть преобразована в (x, y, z) обычным способом

x = r * sin( theta) * cos( phi )
y = r * sin( theta) * sin( phi )
z = r * cos( theta )
34

создайте набор точек, равномерно распределенных внутри куба, затем отбросьте те, расстояние от центра которых превышает радиус желаемой сферы.

14

есть блестящий способ генерировать равномерно точки На сфере в n-мерном пространстве, и вы указали на это в своем вопросе (я имею в виду код MATLAB).

почему это работает? Ответ: давайте посмотрим на плотность вероятности n-мерного нормального распределения. Он равен (до константы)

exp(-x_1*x_1/2) *exp (- x_2*x_2/2)... = exp (- r*r / 2), так что это не зависит от направления, только от расстояния! Это означает, что после нормализации вектора, в результате плотность распределения будет постоянной по всей сфере.

этот метод должен быть определенно предпочтительным из-за его простоты, общности и эффективности (и красоты). Код, который генерирует 1000 событий on сферы в трех измерениях:

size = 1000
n = 3 # or any positive integer
x = numpy.random.normal(size=(size, n)) 
x /= numpy.linalg.norm(x, axis=1)[:, numpy.newaxis]

кстати, хорошая ссылка для просмотра:http://www-alg.ist.hokudai.ac.jp~jan / randsphere.pdf

Что касается равномерного распределения внутри сфера, вместо нормализации вектора вы должны умножить vercor на некоторый f(r): f (r)*r распределяется с плотностью, пропорциональной r^n на [0,1], что было сделано в коде, который вы разместили

12

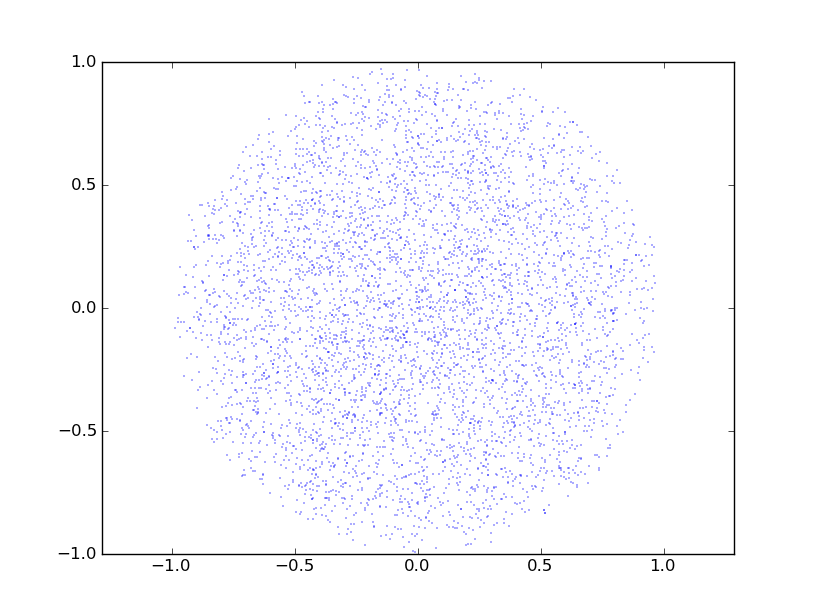
будет ли это достаточно однородным для ваших целей?

In []: p= 2* rand(3, 1e4)- 1
In []: p= p[:, sum(p* p, 0)** .5<= 1]
In []: p.shape
Out[]: (3, 5216)

кусок

In []: plot(p[0], p[2], '.')

похоже,: enter image description here

2

нормированный гауссовский 3d-вектор равномерно распределен по сфере, см. http://mathworld.wolfram.com/SpherePointPicking.html

например:

N = 1000
v = numpy.random.uniform(size=(3,N)) 
vn = v / numpy.sqrt(numpy.sum(v**2, 0))
2

вы можете просто генерировать случайные точки в сферических координатах (предполагая, что вы работаете в 3D): S(r, φ, φ), где r [[0, R), θ ∈ [0, π], φ [[0, 2π), где r-радиус вашей сферы. Это также позволит вам напрямую контролировать, сколько точек генерируется (т. е. вам не нужно отбрасывать какие-либо точки).

чтобы компенсировать потерю плотности радиусом, вы генерируете радиальную координату после распределения по закону мощности (см. ответ dmckee для объяснения того,как это сделать).

Если вашему коду нужны (x,y,z) (т. е. декартовые) координаты, вы просто преобразуете случайно сгенерированные точки в сферических в декартовых координатах, как объяснено здесь.

-1

import numpy as np
import matplotlib.pyplot as plt





r= 30.*np.sqrt(np.random.rand(1000))
#r= 30.*np.random.rand(1000)
phi = 2. * np.pi * np.random.rand(1000)



x = r * np.cos(phi)
y = r * np.sin(phi)


plt.figure()
plt.plot(x,y,'.')
plt.show()

это то, что вы хотите

-1