вычисление точки пересечения квадратичной кривой Безье

Это определенно раздвигает границы моих знаний тригонометрии.

существует ли формула для вычисления точки пересечения между квадратичной кривой Безье и линией?

пример:

на изображении ниже у меня есть P1, P2, C (который является контрольной точкой) и X1, X2 (который для моего конкретного расчета является просто прямой линией на оси X.)

то, что я хотел бы знать, - это положение X, Y T, а также угол касательной в точке T. В точке пересечения между Красной кривой и черной линией.

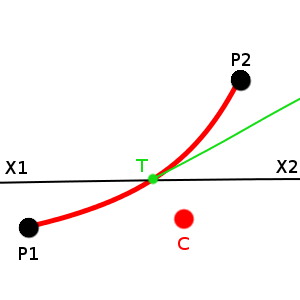
curve example

после небольшого исследования и поиска этой вопрос, я знаю, что могу использовать:

t = 0.5; // given example value
x = (1 - t) * (1 - t) * p[0].x + 2 * (1 - t) * t * p[1].x + t * t * p[2].x;
y = (1 - t) * (1 - t) * p[0].y + 2 * (1 - t) * t * p[1].y + t * t * p[2].y;

для вычисления моего положения X, Y в любой заданной точке вдоль кривой. Таким образом, используя это, я мог бы просто пройти через кучу точек вдоль кривой, проверяя, есть ли они на моей пересекающейся оси X. И оттуда попробуй вычислить мою касательную. угол. Но это действительно не кажется лучшим способом сделать это. Любой математический гуру знает, что лучше всего?

Я думаю, что, возможно, это немного сложнее, чем я хочу быть.

6
canvas html5 javascript trigonometry

2 ответов

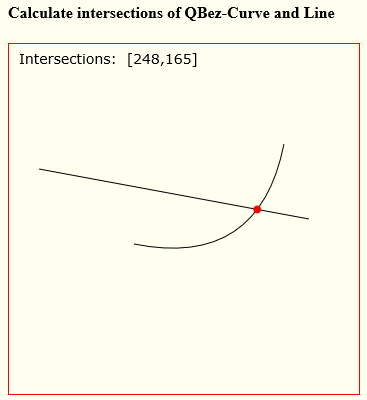
enter image description here

Формула квадратичной кривой:

y=ax^2+bx+c // where a,b,c are known

строка формулы:

// note: this `B` is not the same as the `b` in the quadratic formula ;-)

y=m*x+B  // where m,B are known.

кривая и линия пересекаются, где оба уравнения истинны для одного и того же [x, y]:

вот аннотированный код и демо:

// canvas vars
var canvas=document.getElementById("canvas");
var ctx=canvas.getContext("2d");
var cw=canvas.width;
var ch=canvas.height;

// linear interpolation utility
var lerp=function(a,b,x){ return(a+x*(b-a)); };

// qCurve & line defs
var p1={x:125,y:200};
var p2={x:250,y:225};
var p3={x:275,y:100};
var a1={x:30,y:125};
var a2={x:300,y:175};

// calc the intersections
var points=calcQLintersects(p1,p2,p3,a1,a2);

// plot the curve, line & solution(s)
var textPoints='Intersections: ';
ctx.beginPath();
ctx.moveTo(p1.x,p1.y);
ctx.quadraticCurveTo(p2.x,p2.y,p3.x,p3.y);
ctx.moveTo(a1.x,a1.y);
ctx.lineTo(a2.x,a2.y);
ctx.stroke();
ctx.beginPath();
for(var i=0;i<points.length;i++){
  var p=points[i];
  ctx.moveTo(p.x,p.y);
  ctx.arc(p.x,p.y,4,0,Math.PI*2);
  ctx.closePath();
  textPoints+=' ['+parseInt(p.x)+','+parseInt(p.y)+']';
}
ctx.font='14px verdana';
ctx.fillText(textPoints,10,20);
ctx.fillStyle='red';
ctx.fill();

///////////////////////////////////////////////////

function calcQLintersects(p1, p2, p3, a1, a2) {
  var intersections=[];

  // inverse line normal
  var normal={
    x: a1.y-a2.y,
    y: a2.x-a1.x,
  }

  // Q-coefficients
  var c2={
    x: p1.x + p2.x*-2 + p3.x,
    y: p1.y + p2.y*-2 + p3.y
  }

  var c1={
    x: p1.x*-2 + p2.x*2,
    y: p1.y*-2 + p2.y*2,
  }

  var c0={
    x: p1.x,
    y: p1.y
  }

  // Transform to line 
  var coefficient=a1.x*a2.y-a2.x*a1.y;
  var a=normal.x*c2.x + normal.y*c2.y;
  var b=(normal.x*c1.x + normal.y*c1.y)/a;
  var c=(normal.x*c0.x + normal.y*c0.y + coefficient)/a;

  // solve the roots
  var roots=[];
  d=b*b-4*c;
  if(d>0){
    var e=Math.sqrt(d);
    roots.push((-b+Math.sqrt(d))/2);
    roots.push((-b-Math.sqrt(d))/2);
  }else if(d==0){
    roots.push(-b/2);
  }

  // calc the solution points
  for(var i=0;i<roots.length;i++){
    var minX=Math.min(a1.x,a2.x);
    var minY=Math.min(a1.y,a2.y);
    var maxX=Math.max(a1.x,a2.x);
    var maxY=Math.max(a1.y,a2.y);
    var t = roots[i];
    if (t>=0 && t<=1) {
      // possible point -- pending bounds check
      var point={
        x:lerp(lerp(p1.x,p2.x,t),lerp(p2.x,p3.x,t),t),
        y:lerp(lerp(p1.y,p2.y,t),lerp(p2.y,p3.y,t),t)
      }
      var x=point.x;
      var y=point.y;
      // bounds checks
      if(a1.x==a2.x && y>=minY && y<=maxY){  
        // vertical line
        intersections.push(point);
      }else if(a1.y==a2.y && x>=minX && x<=maxX){
        // horizontal line
        intersections.push(point);
      }else if(x>=minX && y>=minY && x<=maxX && y<=maxY){
        // line passed bounds check
        intersections.push(point);
      }
    }
  }
  return intersections;
}
body{ background-color: ivory; padding:10px; }
#canvas{border:1px solid red;}
<h4>Calculate intersections of QBez-Curve and Line</h4>
<canvas id="canvas" width=350 height=350></canvas>
4

Если вам нужно только пересечение с прямой линией в направлении x, вы уже знаете координату Y пересечения. Чтобы получить координату x, сделайте что-то вроде этого:

  • уравнение для вашей линии просто y = b
  • установив его равным ваше y-уравнение функции beziér y(t) получает вас:
    b = (1 - t) * (1 - t) * p[0].y + 2 * (1 - t) * t * p[1].y + t * t * p[2].y
  • решение* для t получает вас:
    t = (p[0].y - p[1].y - sqrt(b*a + p[1].y*p[1].y - p[0].y*p[2].y)) / a
    с a = p[0].y - 2*p[1].y + p[2].y
  • вставить полученный t на ваш х-уравнение функции beziér x(t) чтобы получить X-координату, и вы сделали.

возможно, вам придется обратить внимание на некоторые особые случаи, например, когда нет решения, потому что аргумент квадратного корня может стать отрицательным или знаменателем (a) может стать нулем или что-то в этом роде.

оставьте комментарий, если вам нужна дополнительная помощь или пересечения с произвольной линии.

(*) я использовал Wolfram alpha для решения уравнение, потому что я ленив:Вольфрам Альфа решение.

4