Вычислить объем любого тетраэдра с учетом 4 точек

Мне нужно рассчитать объем" любого " тетраэдра с учетом 4 точек. Я пишу программу, которая должна найти объем тетраэдра, и я знаю, что: все X, Y, Z расположение 4 точек. Функция должна вернуть объем. Я застрял в этом на 10 часов... Я ни о чем не мог думать. Спасибо!

7
3d geometry math

4 ответов

скажем, если у вас есть 4 вершины a,b,c,d (3-D векторы).

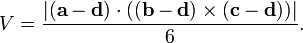
enter image description here

Итак, проблема сводится к написанию кода, который решает векторное произведение и скалярное произведение векторов. Если вы из python, вы можете использовать NumPy или написать код самостоятельно.

ссылка Wikipedia определенно должна вам помочь. ссылке

14

один из способов вычисления этого тома:

     1      [ax bx cx dx]
V = --- det [ay by cy dy]
     6      [az bz cz dz]
            [ 1  1  1  1]

Это включает в себя оценку определителя 4×4. Он хорошо обобщается на симплексы более высоких размеров, причем 6 является частным случаем n!, факториал измерения. Результирующий объем будет ориентацией, т. е. может быть отрицательным в зависимости от заказа очков. Если вы этого не хотите, возьмите абсолютное значение результата.

Если у вас есть математическая библиотека под рукой, вышеуказанная формулировка может быть одной из самых простых для записи, и программное обеспечение может взять ее оттуда. Если нет, вы можете сначала упростить вещи, вычитая d координаты a через c. Это не изменит громкость, но превратит самый правый столбец в (0, 0, 0, 1). В результате вы можете вычислить значение матрицы просто как определитель верхней левой подматрицы 3×3. И используя уравнение

det(a, b, c) = a · (b × c)

вы в конечном итоге с формулой от Сурья ответ.

Если у вас нет координат для точек, но просто расстояния между ними, посмотрите на Формула Тарталья что по существу является квадратной версией вышеизложенного, хотя это не так прямолинейно, как казалось бы на первый взгляд.

7

пример Ивана Зайделя, в Python (ответ 1.3333...)

def determinant_3x3(m):
    return (m[0][0] * (m[1][1] * m[2][2] - m[1][2] * m[2][1]) -
            m[1][0] * (m[0][1] * m[2][2] - m[0][2] * m[2][1]) +
            m[2][0] * (m[0][1] * m[1][2] - m[0][2] * m[1][1]))


def subtract(a, b):
    return (a[0] - b[0],
            a[1] - b[1],
            a[2] - b[2])

def tetrahedron_calc_volume(a, b, c, d):
    return (abs(determinant_3x3((subtract(a, b),
                                 subtract(b, c),
                                 subtract(c, d),
                                 ))) / 6.0)

a = [0.0, 0.0, 0.0]
d = [2.0, 0.0, 0.0]
c = [0.0, 2.0, 0.0]
b = [0.0, 0.0, 2.0]

print(tetrahedron_calc_volume(a, b, c, d))
4

вот код в PHP, который вычисляет объем любого тетраэдра с учетом 4 точек:

class Math{
public static function determinant(array $vals){
    $s = sizeof($vals);
    $sum = 0.0;
    for( $i=0; $i < $s ; $i++ ){
        $mult = 1.0;
        for($j=0; $j < $s ; $j++ ){
            $mult *= $vals[$j][ ($i+$j)%$s ];
        }
        $sum += $mult;
    }
    for( $i=0; $i < $s ; $i++ ){
        $mult = 1;
        for($j=0; $j < $s ; $j++ ){
            $mult *= $vals[$j][ ($i-$j < 0? $s - ($j-$i) :($i-$j)) ];
        }
        $sum -= $mult;
    }
    return $sum;
}

public static function subtract(array $a, array $b){
    for($i = 0; $i < sizeof($a); $i++)
        $a[$i] -= $b[$i];

    return $a;
}
}
// TEST CASE
$a = array(0,0,0);
$d = array(2,0,0);
$c = array(0,2,0);
$b = array(0,0,2);

echo abs(Math::determinant(array(
Math::subtract($a, $b),
Math::subtract($b, $c),
Math::subtract($c, $d),
)))/6;
1