Вычислить PI, используя сумму обратных квадратов
Мне нужно рассчитать PI с предопределенной точностью, используя эту формулу:
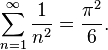
Итак, я закончил с этим решением.
private static double CalculatePIWithPrecision(int presicion)
{
if (presicion == 0)
{
return PI_ZERO_PRECISION;
}
double sum = 0;
double numberOfSumElements = Math.Pow(10, presicion + 2);
for (double i = 1; i < numberOfSumElements; i++)
{
sum += 1 / (i * i);
}
double pi = Math.Sqrt(sum * 6);
return pi;
}
Так что это работает правильно, но я столкнулся с проблемой эффективности. Это очень медленно со значениями точности 8 и выше.
есть ли лучше (и быстрее!) способ вычисления PI с использованием этой формулы?
1 ответов
double numberOfSumElements = Math.Pow(10, presicion + 2);
Я собираюсь говорить об этом строго в практических терминах разработки программного обеспечения, избегая заблудиться в формальной математике. Просто практические советы, которые должен знать любой программист.
Сначала обратите внимание на сложность вашего кода. Время выполнения строго определяется этим выражением. Вы написали экспоненциальный алгоритм, значение вы вычисляете очень быстро идет вверх, как presicion увеличивается. Вы цитируете неудобное число, 8 производит 10^10 или цикл, который делает десять миллиардов расчетов. Да, вы замечаете это, когда компьютеры начинают принимать секунды для получения результата, независимо от того, насколько они быстры.
экспоненциальные алгоритмы плохо, они работают очень плохо. Вы можете сделать только хуже, имеющего факторный сложность, O (n!), что идет еще быстрее. В противном случае сложность многих реальных проблемы.
теперь, это выражение действительно точно? Вы можете сделать это с помощью "теста локтя", используя практический пример задней части конверта. Давайте выберем точность 5 цифр в качестве цели и запишем ее:
1.0000 + 0.2500 + 0.1111 + 0.0625 + 0.0400 + 0.0278 + ... = 1.6433
вы можете сказать, что дополнения быстро становятся меньше, это сходится быстро. Вы можете рассудить, что, как только следующее число, которое вы добавляете, становится достаточно маленьким, оно делает очень мало, чтобы сделать результат более точным. Скажем так, когда следующее число меньше 0.00001, тогда пришло время прекратить попытки улучшить результат.
таким образом, вы остановитесь на 1 / (n * n) = 0.00001 => n * n = 100000 => n = sqrt(100000) => n ~= 316
ваше выражение говорит остановится 10^(5+2) = 10,000,000
Вы можете сказать, что вы путь выкл, зацикливаясь слишком часто и не улучшая точность результата с последними 9.999 миллионами итераций.
время поговорить о реальных проблема, жаль, что вы не объяснили, как вы попали в такой радикально неправильный алгоритм. Но, конечно, вы обнаружили при тестировании своего кода, что он просто не очень хорошо вычисляет более точное значение для pi. Поэтому вы решили, что, повторяя чаще, вы получите лучший результат.
обратите внимание, что в этом локтевом тесте также очень важно, чтобы вы могли рассчитать дополнения с достаточной точностью. Я намеренно округлил цифры, как будто это был высчитано на машине способной выполнять дополнения с 5 числами точности. Что бы вы ни делали, результат никогда не может быть больше точный чем 5 чисел.
вы используете двойной вводите свой код. Непосредственно поддерживается процессором, он не имеет бесконечной точности. Единственное правило, которое вам когда-либо нужно иметь в виду, - это расчеты с двойной никогда не являются более точными, чем 15 цифр. Также запомните правило для float, он никогда не бывает более точным, чем 7 цифр.
поэтому независимо от того, какое значение вы прослывете presicion, результат никогда быть более точным, чем 15 цифр. Это совсем не полезно, у вас уже есть значение pi с точностью до 15 цифр. Это математика.Пи
единственное, что вам нужно сделать, чтобы исправить это, это использовать тип, который имеет большую точность, чем двойной. На самом деле, это должен быть тип, который имеет произвольные точность, она должна быть по крайней мере так же точна, как presicion стоимостью вы пройти. Такой тип не существует в .NET framework. Поиск библиотеки, которая может предоставить вам один, - это общий вопрос at SO.
