Алгоритм интерполяции ближайшего соседа в MATLAB

Я пытаюсь написать свою собственную функцию для масштабирования входного изображения с помощью алгоритма ближайшего соседа, интерполяция. Плохо то, что я могу видеть, как он работает, но не могу найти сам алгоритм. Буду благодарен за любую помощь.

вот что я пытался масштабировать входное изображение в 2 раза:

function output = nearest(input)
[x,y]=size(input);
output = repmat(uint8(0),x*2,y*2);
[newwidth,newheight]=size(output);
for i=1:y
    for j=1:x
        xloc = round ((j * (newwidth+1)) / (x+1));
        yloc = round ((i * (newheight+1)) / (y+1));
        output(xloc,yloc) = input(j,i);
    end
end

вот вывод после Марк'предложение з alt text

20
image-processing interpolation matlab nearest-neighbor resize-image

4 ответов

некоторое время назад я прошел через код imresize

19

этот ответ более толковый, чем пытаться быть кратким и эффективным. Я думаю gnoviceрешение лучше всего в этом отношении. Если вы пытаетесь понять, как это работает, продолжайте читать...

теперь проблема с вашим кодом заключается в том, что вы сопоставляете местоположения с входного изображения на выходное изображение, поэтому вы получаете пятнистой выход. Рассмотрим пример, когда входное изображение все белое, а выход инициализирован черным, мы получите следующее:

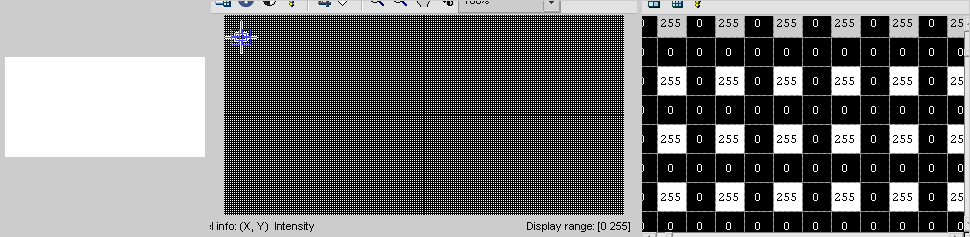
screenshot

то, что вы должны делать, противоположно (от выхода до входа). Для иллюстрации рассмотрим следующие обозначения:

1           c         1                 scaleC*c
+-----------+ 1       +----------------------+ 1
|    |      |         |        |             |
|----o      |   <===  |        |             |
|  (ii,jj)  |         |--------o             |
+-----------+ r       |      (i,j)           |
  inputImage          |                      |
                      |                      |
                      +----------------------+ scaleR*r
                            ouputImage

Note: I am using matrix notation (row/col), so:
  i ranges on [1,scaleR*r] , and j on [1,scaleC*c]
  and ii on [1,r], jj on [1,c]

идея в том, что для каждого местоположения (i,j) в выходном изображении мы хотим сопоставить его с "ближайшим" местоположением во входных координатах изображения. Поскольку это простое отображение, мы используем формулу, которая отображает заданное x to y (учитывая все остальные params):

 x-minX      y-minY
--------- = ---------
maxX-minX   maxY-minY

в нашем случае, x - это i/j координировать и y - это ii/jj координат. Поэтому подстановка для каждого дает нам:

jj = (j-1)*(c-1)/(scaleC*c-1) + 1
ii = (i-1)*(r-1)/(scaleR*r-1) + 1

складывая кусочки вместе, получаем следующий код:

% read a sample image
inputI = imread('coins.png');
[r,c] = size(inputI);
scale = [2 2];        % you could scale each dimension differently

outputI = zeros(scale(1)*r,scale(2)*c, class(inputI));

for i=1:scale(1)*r
    for j=1:scale(2)*c
        % map from output image location to input image location
        ii = round( (i-1)*(r-1)/(scale(1)*r-1)+1 );
        jj = round( (j-1)*(c-1)/(scale(2)*c-1)+1 );

        % assign value
        outputI(i,j) = inputI(ii,jj);
    end
end

figure(1), imshow(inputI)
figure(2), imshow(outputI)
20

MATLAB уже сделал это за вас. Использовать imresize:

output = imresize(input,size(input)*2,'nearest');

или если вы хотите масштабировать оба X и y одинаково,

output = imresize(input,2,'nearest');
2

вам просто нужна более обобщенная формула для вычисления xloc и yloc.

xloc = (j * (newwidth+1)) / (x+1);
yloc = (i * (newheight+1)) / (y+1);

при этом предполагается, что переменные имеют достаточный диапазон для результатов умножения.

0