Алгоритм пикового поиска для Python/SciPy

Я смотрю на аналогичную проблему, и я нашел некоторые из лучших ссылок из химии (от пиков, найденных в данных масс-спецификации). Для хорошего тщательного обзора алгоритмов поиска пиков прочитайте этой. Это один из лучших четких обзоров методов поиска пиков, с которыми я сталкивался. (Вейвлеты являются лучшими для поиска пиков такого рода в шумных данных.).

похоже, что ваши пики четко определены и не скрыты в шуме. Что в этом случае я бы рекомендовал использовать гладкие производные савтизки-голая, чтобы найти пики (если вы просто дифференцируете данные выше, у вас будет беспорядок ложных срабатываний.). Это очень эффективный метод и довольно прост в реализации (вам нужен матричный класс с базовыми операциями). Если вы просто найдете нулевое пересечение первой производной S-G, я думаю, вы будете счастливы.

в scipy есть функция с именем scipy.signal.find_peaks_cwt который звучит как подходит для ваших нужд, однако у меня нет опыта работы с ним, поэтому я не могу рекомендовать..

http://docs.scipy.org/doc/scipy/reference/generated/scipy.signal.find_peaks_cwt.html

для тех, кто не уверен, какие алгоритмы поиска пиков использовать в Python, здесь Быстрый обзор альтернатив:https://github.com/MonsieurV/py-findpeaks

желая себе эквивалент MatLab

обнаружение пиков в спектре надежным способом было изучено совсем немного, например, вся работа по синусоидальному моделированию для музыкальных/звуковых сигналов в 80-х годах. Ищите "синусоидальное моделирование" в литературе.

Если ваши сигналы так же чисты, как пример, простое "дайте мне что-то с амплитудой выше, чем N соседей" должно работать достаточно хорошо. Если у вас есть шумные сигналы, простой, но эффективный способ-посмотреть на ваши пики во времени, отследить их: вы затем обнаружить спектральные линии вместо спектральных пиков. IOW, вы вычисляете БПФ на скользящем окне вашего сигнала, чтобы получить набор спектра во времени (также называемый спектрограммой). Затем вы смотрите на эволюцию спектрального пика во времени (т. е. в последовательных окнах).

функции scipy.signal.find_peaks, как следует из названия, полезно для этого. Но важно хорошо понимать его параметры width, threshold, distance и главное prominence получить хорошее пиковое извлечение.

согласно моим тестам и документации, концепция протуберанец "полезная концепция" для того чтобы держать хорошие пики, и сбрасывает шумные пики.

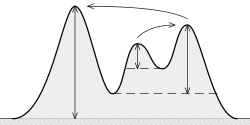
что это (кадастровый) известность? Это "минимальная высота, необходимая для спуска с вершины на любую более высокую местность", как видно здесь:

идея:

чем выше видимость, тем более "важным" является пик.

тест:

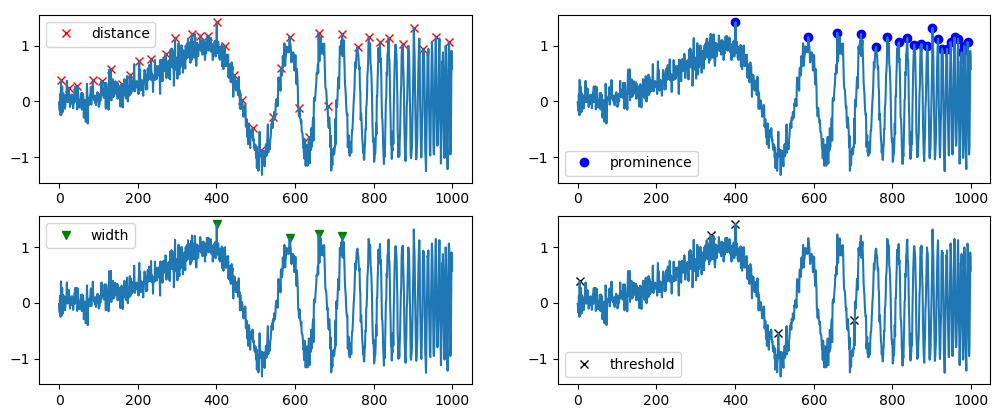
я использовал (шумный) частотно-изменяющийся синусоид специально, потому что он показывает много трудностей. Мы видим, что width параметр здесь не очень полезен, потому что если вы установите минимум width слишком высоко, тогда он не сможет отслеживать очень близкие пики в высокочастотной части. Если вы установите width слишком низко, у вас будет много нежелательных пиков в левой части сигнала. Та же проблема с distance. threshold сравнивает только с прямыми соседями, что здесь не полезно. prominence - это тот, который дает лучшее решение. Обратите внимание, что вы можете объединить многие из эти параметры!

код:

import numpy as np
import matplotlib.pyplot as plt 
from scipy.signal import find_peaks, find_peaks_cwt

x = np.sin(2*np.pi*(2**np.linspace(2,10,1000))*np.arange(1000)/48000) + np.random.normal(0, 1, 1000) * 0.15
peaks, _ = find_peaks(x, distance=20)
peaks2, _ = find_peaks(x, prominence=1)      # BEST!
peaks3, _ = find_peaks(x, width=20)
peaks4, _ = find_peaks(x, threshold=0.4)     # Required vertical distance to its direct neighbouring samples, pretty useless
plt.subplot(2, 2, 1)
plt.plot(peaks, x[peaks], "xr"); plt.plot(x); plt.legend(['distance'])
plt.subplot(2, 2, 2)
plt.plot(peaks2, x[peaks2], "ob"); plt.plot(x); plt.legend(['prominence'])
plt.subplot(2, 2, 3)
plt.plot(peaks3, x[peaks3], "vg"); plt.plot(x); plt.legend(['width'])
plt.subplot(2, 2, 4)
plt.plot(peaks4, x[peaks4], "xk"); plt.plot(x); plt.legend(['threshold'])
plt.show()

существуют стандартные статистические функции и методы для обнаружения выбросов в данные, что, вероятно, вам нужно в первом случае. Использование производных решит вашу вторую. Однако я не уверен в методе, который решает как непрерывные функции, так и выборочные данные.

во-первых, определение "пика" является расплывчатым, если без дополнительных спецификаций. Например, для следующей серии, вы бы назвали 5-4-5 один пик или два?

1-2-1-2-1-1-5-4-5-1-1-5-1

в этом случае вам понадобится как минимум два порога: 1) высокий порог, выше которого экстремальное значение может регистрироваться как пик; и 2) низкий порог, так что экстремальные значения, разделенные небольшими значениями ниже, станут двумя пиками.

пик обнаружение-хорошо изученная тема в литературе по теории экстремальных ценностей, также известная как "декластеризация экстремальных ценностей". Свои типичные применения включают определять события опасности основанные на непрерывных чтениях переменных окружающей среды например анализируя скорости ветра для того чтобы обнаружить события шторма.