Алгоритм "разделяй и властвуй" для подсчета доминирующих точек?
предположим, что точка в координате (x1, y1) возвышается другая точка (x2,y2), если x1 ≤ x2 и y1 ≤ y2;
У меня есть набор точек (x1, y1),....(xn, yn) и я хочу найти общее количество доминирующих пар. Я могу сделать это, используя грубую силу, сравнивая все точки друг с другом, но для этого требуется время O (n2). Вместо этого я хотел бы использовать подход "разделяй и властвуй", чтобы решить это во времени O(n log n).
прямо сейчас у меня есть следующий алгоритм:
нарисуйте вертикальную линию, разделяющую множество точек точек на два равных подмножества Рлевый и Pправо. В качестве базового случая, если осталось всего две точки, я могу сравнить их напрямую.
рекурсивно подсчитайте количество доминирующих пар в Pлевый и Pправо
некоторые покорять шаг?
проблема в том, что я не вижу, какой шаг "завоевать" должен быть здесь. Я хочу подсчитать, сколько доминирующих пар есть, что крест от Pлевый в Pправо, но я не знаю, как это сделать, не сравнивая все точки в обеих частях, что займет время O (n2).
может кто-нибудь дать мне подсказку о том, как сделать завоевание шаг?
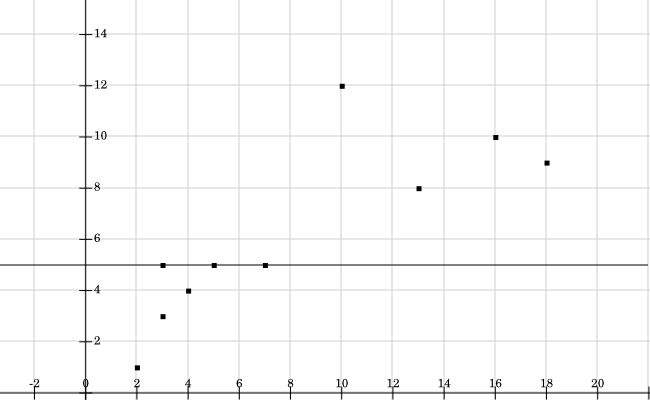
Итак, 2 половины координат y являются : {1,3,4,5,5} и {5,8,9,10,12}
Я провожу линию деления.
3 ответов
Предположим, вы сортируете точки в обеих половинах отдельно в порядке возрастания по их координатам Y. Теперь посмотрите на самую низкую y-значную точку в обеих половинах. Если самая низкая точка слева имеет меньшее значение y, чем самая низкая точка справа, то в этой точке доминируют все точки справа. В противном случае нижняя точка справа не доминирует ни над чем слева.
в любом случае вы можете удалить одну точку из одной из двух половин и повторить процесс с оставшимися отсортированными списками. Это O(1) работает на точку, поэтому, если есть N общих точек, Это O (n) работает (после сортировки), чтобы подсчитать количество доминирующих пар через две половины. Если вы видели это раньше, это похоже на алгоритм подсчета инверсий в массиве).
Факторинг времени, необходимого для сортировки точек (O(N log n)), этот шаг завоевания занимает O (n log n) времени, что дает повторение
T(n) = 2T(n / 2) + O (N log n)
Это решает до O (N log2 n) согласно Главная Теорема.
тем не менее, вы можете ускорить это. Предположим, что перед тем, как начать разделять и покорять, вы заранее задаете точки по их координатам y, выполняя один проход O(N log n). Используя трюки, похожие на ближайшую проблему с парой точек, вы можете получить точки в каждой половине, отсортированной в O (n) раз по каждой подзадаче размера n (см. обсуждение внизу этой страницы) для деталей). Это изменяет повторение на
T(n) = 2T(n / 2) + O (n)
который решает O (N log n), как требуется.
надеюсь, что это помогает!
Ну, таким образом, у вас есть O(n^2) только для деления на подмножества...
Мой подход был бы другим
- сортировать точки по X ... O (n.log (n))
- теперь проверьте Y
- но проверьте только точки с большим X (если вы сортируете их по возрастанию, то с большим индексом)
- Итак, теперь у вас есть O (n.log(n)+(n.n / 2))
вы также можете ускорить процесс, выполнив отдельный тест X и Y и после этого объедините результат, который приведет O (n + 3.n.log (n))
- добавить атрибут индекса к вашим точкам
- где index = 0xyyyyyxxxxh-целочисленный тип без знака
- гггг-индекс точки в y-сортированном массиве
- XXXX-индекс точки в X-сортированном массиве
- если у вас более 2^16 точек, используйте больше, чем 32-битный тип данных.
- сортировать точки по возрастанию X и установить XXXX часть их индекса O1 (n.log (n))
- сортировать точки по возрастанию Y и установить гггг часть их индекса O2 (n.log (n))
- сортировка точек по возрастанию индекса O3(n.log (n))
- теперь точка i доминирует над любой точкой J, Если (i
- но если вам нужно создать фактически все пары для любой точки
- это займет O4 (n.n / 2) таким образом, этот подход сэкономит не мало времени
- если вам нужна только одна пара для любой точки, то простой цикл хватит O4 (n-1)
- Итак, в этом случае O (n-1+3.n.log (n)) - > ~O(n+3.n.log (n))
надеюсь, что это помогло,... конечно, если вы застряли с этим подходом подразделения, чем у меня нет лучшего решения для вас.
PS. для этого вам не нужна дополнительная рекурсия, просто 3x сортировка и только один uint для любой точки, поэтому требования к памяти не так велики и даже должны быть быстрее, чем рекурсивный вызов рекурсии подразделения в целом
этот алгоритм работает в O(N*log (N)) где N-размер списка точек и он использует O (1) дополнительное пространство.
выполните следующие действия:
- сортировка списка точек по координате y (по возрастанию), разрыв связей по X-координата (в порядке возрастания).
- перейдите по отсортированному списку в обратном порядке, чтобы подсчитать доминирующие точки: если текущее значение X-координаты >= max X-координаты встречается так далеко затем увеличьте результат и обновите max.
это работает, так как вы точно знаете, что если все пары с большими координатами y имеют меньшую координату x, чем текущая точка, вы нашли доминирующие точки. Этап сортировки делает его действительно эффективным.
вот код Python:
def my_cmp(p1, p2):
delta_y = p1[1] - p2[1]
if delta_y != 0:
return delta_y
return p1[0] - p2[0]
def count_dom_points(points):
points.sort(cmp = my_cmp)
maxi = float('-inf')
count = 0
for x, y in reversed(points):
if x >= maxi:
count += 1
maxi = x
return count
