Алгоритм решения точек равномерно распределенной / четной спирали?

во-первых, чтобы дать визуальное представление о том, что мне нужно, вот самый близкий результат (но не совсем то, что мне нужно), который я нашел:

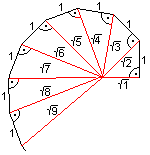
enter image description here

вот весь сайт-ссылка:http://www.mathematische-basteleien.de/spiral.htm

но это не совсем решает проблему, которую я ищу. Я хотел бы сохранить массив точек Очень специфического спирального алгоритма.

  • точки равномерно распределено
  • циклы 360 градусов имеют даже зазор

Если я не ошибаюсь, первые два пункта будут:

  • point[ 0] = новая точка(0,0);
  • point[ 1] = новая точка (1,0);

но куда идти?

единственные аргументы, которые я хотел бы предоставить:

  • количество точек, которые я хочу разрешить (длина массива).
  • расстояние между каждая точка (разрыв пикселей).
  • расстояние между циклами.

Мне почти кажется, что я должен вычислить "спираль-окружность" (если есть такой термин), чтобы построить равномерно распределенные точки вдоль спирали.

Can 2*PI * radius надежно использовать для этого расчета вы думаете?

Если это было сделано раньше, пожалуйста, покажите пример кода!

7
actionscript-3 algorithm math pseudocode spiral

2 ответов

забавная маленькая проблема:)

если вы посмотрите на диаграмму ближе, последовательность четко указана:

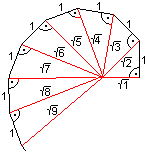
spiral diagram

вероятно, есть много решений для рисования этих, может быть, более элегантных, но вот мой:

вы знаете, гипотенуза равно корню из текущего сегмента+1 а противоположная сторона треугольника всегда равна 1.

также вы знаете, что синус(математика.sin) угла равна противоположной стороне, разделенной на гипотенуза. от старого мненонического SOH (синус, противоположный, гипотенуза),-CAH-TOA.

Math.sin(angle) = opp/hyp

вы знаете значение синуса для угла, вы знаете две стороны, но вы еще не знаете угол, но вы можете использовать функцию синуса дуги(математика.Асин) за это

angle = Math.asin(opp/hyp)

теперь вы знаете угол для каждого сегмента и замечаете, что он увеличивается с каждой линией.

теперь, когда у вас есть угол и радиус (гипотенуза), вы можете использовать для полярный для декартовой формула для преобразования, что угол,радиус пару x, y пара.

x = Math.cos(angle) * radius;
y = Math.sin(angle) * radius;

поскольку вы запросили решение actionscript, класс Point уже предоставляет эту функцию для вас через polar() метод. Вы передаете ему радиус и угол, и он возвращает ваши x и y в точечном объекте.

вот небольшой фрагмент, который строит спираль. Вы можете управлять количеством сегментов, перемещая мышь на y-оси.

var sw:Number = stage.stageWidth,sh:Number = stage.stageHeight;
this.addEventListener(Event.ENTER_FRAME,update);
function update(event:Event):void{
    drawTheodorus(144*(mouseY/sh),sw*.5,sh*.5,20);
}
//draw points
function drawTheodorus(segments:int,x:Number,y:Number,scale:Number):void{
    graphics.clear();
    var points:Array = getTheodorus(segments,scale);
    for(var i:int = 0 ; i < segments; i++){
        points[i].offset(x,y);
        graphics.lineStyle(1,0x990000,1.05-(.05+i/segments));
        graphics.moveTo(x,y);//move to centre
        graphics.lineTo(points[i].x,points[i].y);//draw hypotenuse
        graphics.lineStyle(1+(i*(i/segments)*.05),0,(.05+i/segments));
        if(i > 0) graphics.lineTo(points[i-1].x,points[i-1].y);//draw opposite
    }
}
//calculate points
function getTheodorus(segments:int = 1,scale:Number = 10):Array{
    var result = [];
    var radius:Number = 0;
    var angle:Number = 0;
    for(var i:int = 0 ; i < segments ; i++){
        radius = Math.sqrt(i+1);
        angle += Math.asin(1/radius);//sin(angle) = opposite/hypothenuse => used asin to get angle
        result[i] = Point.polar(radius*scale,angle);//same as new Point(Math.cos(angle)*radius.scale,Math.sin(angle)*radius.scale)
    }
    return result;
}

это могло быть написано меньше строк, но я хотел разделить это на две функции: один занимается только вычислением чисел, а другой-рисованием линий.

вот несколько скриншотов:

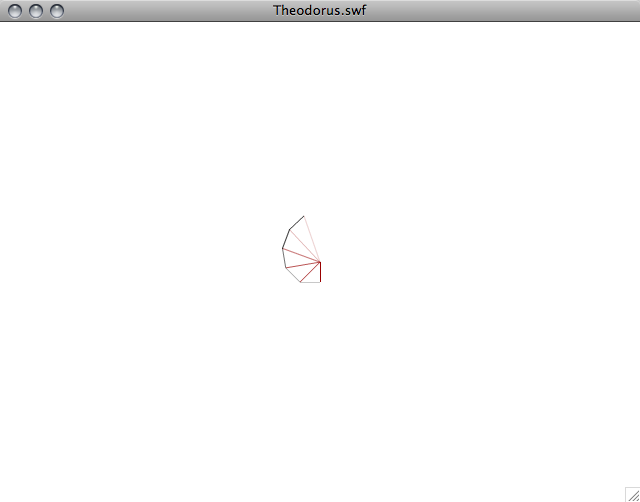
spiral 1

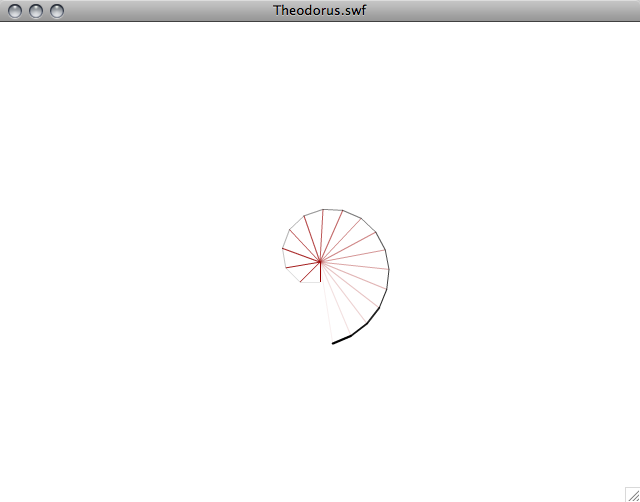
spiral 2

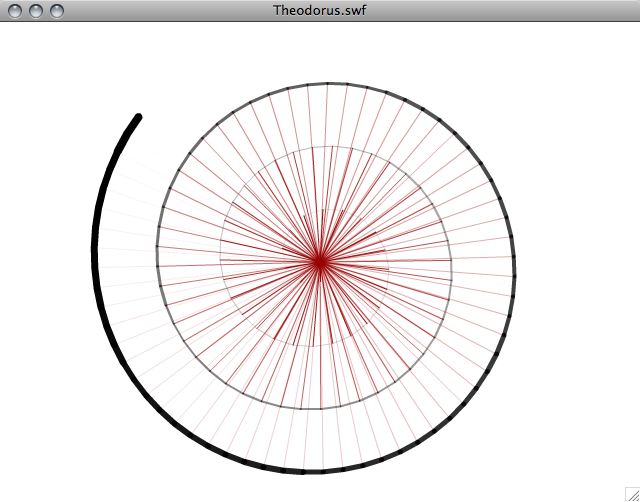
spiral 3

для удовольствия я добавил версию этого с помощью ProcessingJS здесь. Работает немного медленно, поэтому я бы рекомендовал Хром / Хром для этого.

теперь вы можете запустить этот код прямо здесь (переместите мышь вверх и вниз):

var totalSegments = 850,hw = 320,hh = 240,segments;
var len = 10;
points = [];
function setup(){
  createCanvas(640,480);
  smooth();
  colorMode(HSB,255,100,100);
  stroke(0);
  noFill();
  //println("move cursor vertically");
}
function draw(){
  background(0);
  translate(hw,hh);
  segments = floor(totalSegments*(mouseY/height));
  points = getTheodorus(segments,len);
  for(var i = 0 ; i < segments ; i++){
    strokeWeight(1);
    stroke(255-((i/segments) * 255),100,100,260-((i/segments) * 255));
    line(0,0,points[i].x,points[i].y);
    // strokeWeight(1+(i*(i/segments)*.01));
    strokeWeight(2);
    stroke(0,0,100,(20+i/segments));
    if(i > 0) line(points[i].x,points[i].y,points[i-1].x,points[i-1].y);
  }
}
function getTheodorus(segments,len){
  var result = [];
  var radius = 0;
  var angle = 0;
  for(var i = 0 ; i < segments ; i++){
    radius = sqrt(i+1);
    angle += asin(1/radius);
    result[i] = new p5.Vector(cos(angle) * radius*len,sin(angle) * radius*len);
  }
  return result;
}
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/0.4.4/p5.min.js"></script>
18