Библиотека тесселяции C++ 2D?
У меня есть выпуклые многоугольники, хранящиеся как вектор STL точек (более или менее). Я хочу тесселяцию их очень быстро, предпочтительно в довольно равномерно распределенные части, и без "щепок".
Я собираюсь использовать его, чтобы взорвать некоторые объекты на мелкие кусочки. Кто-нибудь знает хорошую библиотеку для мозаики полигонов (разбить их на сетку меньших выпуклых полигонов или треугольников)?
Я посмотрел на некоторые я уже нашел в интернете, но я даже не могу их скомпилировать. Эти академические типы не придают большого значения простоте использования.
7 ответов
CGAL имеет пакеты для решения этой проблемы. Лучше всего было бы, вероятно, использовать 2D полигона разметки. Например, вы можете сгенерировать y-монотонное разбиение многоугольника (работает и для невыпуклых полигонов), и вы получите что-то вроде этого:
y-моноион-разделение http://www.cgal.org/Manual/3.4/doc_html/cgal_manual/Partition_2/Trier_opt_cvx.gif y-моноион-разделение http://www.cgal.org/Manual/3.4/doc_html/cgal_manual/Partition_2/Idar-Oberstein_appx_cvx.gif
время выполнения O (N log n).
С точки зрения простоты использования это небольшой пример кода, генерирующий случайный многоугольник и разделяющий его (на основе этот ручной пример):
typedef CGAL::Exact_predicates_inexact_constructions_kernel K;
typedef CGAL::Partition_traits_2<K> Traits;
typedef Traits::Point_2 Point_2;
typedef Traits::Polygon_2 Polygon_2;
typedef std::list<Polygon_2> Polygon_list;
typedef CGAL::Creator_uniform_2<int, Point_2> Creator;
typedef CGAL::Random_points_in_square_2<Point_2, Creator> Point_generator;
int main( )
{
Polygon_2 polygon;
Polygon_list partition_polys;
CGAL::random_polygon_2(50, std::back_inserter(polygon),
Point_generator(100));
CGAL::y_monotone_partition_2(polygon.vertices_begin(),
polygon.vertices_end(),
std::back_inserter(partition_polys));
// at this point partition_polys contains the partition of the input polygons
return 0;
}
чтобы установить cgal, если вы находитесь в windows, вы можете использовать установщик для получения предварительно скомпилированной библиотеки, и есть руководства по установке для каждой платформы на на этой странице. Возможно, это не самая простая установка, но вы получаете самую используемую и надежную библиотеку вычислительной геометрии, и список рассылки cgal очень полезно отвечать на вопросы...
poly2tri выглядит как очень хорошая легкая библиотека C++ для 2D триангуляции Делоне.
Как Балинт.Миклош упоминал в комментарии выше, Shewchuk это треугольник пакет вполне хорошо. Я сам использовал его много раз; он прекрасно интегрируется в проекты, и есть треугольник++ интерфейс C++. Если вы хотите избежать осколков, то позвольте треугольнику добавить (внутренние) точки Штайнера, чтобы создать качественную сетку (обычно ограниченную соответствующую триангуляцию Делоне).
Если вы не хотите создавать весь GCAL в своем приложении - это, вероятно, проще реализовать.
http://www.flipcode.com/archives/Efficient_Polygon_Triangulation.shtml
Я только начал изучать эту же проблему, и я рассматриваю тесселяцию вороного. Исходный многоугольник получит рассеяние полуслучайных точек, которые будут центрами ячеек вороного, чем более равномерно они распределены, тем более регулярными будут ячейки, но они не должны быть в идеальной сетке, иначе внутренние многоугольники будут выглядеть одинаково. Итак, первое, что нужно сделать, - это сгенерировать эти центральные точки ячейки-сгенерировать их над ограничивающей рамкой исходного полигона и внутреннего/внешнего теста не должно быть слишком сложно.
края вороного являются пунктирными линиями на этом рисунке и являются своего рода дополнением триангуляции Делоне. Все острые точки треугольника притупляются:
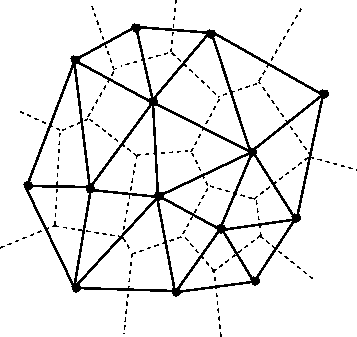
Boost имеет некоторые функции вороного: http://www.boost.org/doc/libs/1_55_0/libs/polygon/doc/voronoi_basic_tutorial.htm
следующим шагом является создание полигонов вороного. Voro++ http://math.lbl.gov/voro++/ ориентирован на 3D, но в другом месте предполагается, что примерно 2d-структура будет работать, но будет намного медленнее, чем программное обеспечение, ориентированное на 2D-вороной. Другой пакет, который выглядит намного лучше, чем случайный проект сироты академической домашней страницы, - этоhttps://github.com/aewallin/openvoronoi.
похоже, что OpenCV использовал для поддержки что-то в этом роде, но он был устаревшим (но c-api все еще работает?). cv:: distTransform по-прежнему поддерживается, но работает с пикселями и генерирует пиксельные выходные данные, а не вершины и структуры данных краевого полигона, но может быть достаточным для моих нужд, если не для ваших.
я обновлю это, как только узнаю больше.
немного более подробно о вашем желаемом входе и выходе может быть полезно.
например, если вы просто пытаетесь получить многоугольники в треугольники, вентилятор треугольника, вероятно, будет работать. Если вы пытаетесь разрезать многоугольник на маленькие кусочки, вы можете реализовать какие-то марширующие квадраты.
хорошо, я сделал плохое предположение - я предположил, что марширующие квадраты будут больше похожи на марширующие Кубы. Оказывается, это совсем другое, и не то, что я имел в виду. все.. :|
в любом случае, чтобы напрямую ответить на ваш вопрос, я не знаю ни одного простого библиотеки, которая делает то, что вы ищете. Я согласен с удобством использования CGAL.
алгоритм, о котором я думал, в основном разделял полигоны с линиями, где линии являются сеткой, поэтому вы в основном получаете квадроциклы. Если бы у вас было пересечение многоугольника с линией, реализация была бы простой. Другим способом постановки этой проблемы является обработка 2d-полигона как функции и наложение сетка точек. Тогда вы просто делаете что-то похожее на марширующие кубики.. если все 4 точки находятся в многоугольнике, сделайте квадрат, если 3 - треугольник,2-прямоугольник и т. д. Наверное, перебор. Если вам нужны слегка нерегулярные полигоны, вы можете рандомизировать местоположения точек сетки.
с другой стороны, вы можете сделать подразделение стиля catmull-clark, но опустить сглаживание. Алгоритм в основном вы добавляете точку в центроиде и в средней точке каждого края. Затем для каждого угла исходного полигона вы создаете новый меньший полигон, который соединяет среднюю точку ребра, предшествующую углу, угол, следующую среднюю точку ребра и центроид. Это плитки пространство, и будет иметь углы, аналогичные вашему входному полигону.
итак, много вариантов, и мне нравятся решения для мозгового штурма, но я все еще не знаю, для чего вы планируете использовать это. Это для создания разрушаемых сеток? Вы делаете какую-то обработку сетки что требует меньших элементов? Пытаясь избежать артефактов затенения Gouraud? Это что-то, что работает как предварительный процесс или в реальном времени? Насколько важна точность? Более подробная информация позволит выработать более эффективные предложения.
Если у вас выпуклые многоугольники, и вы не слишком зациклены на качестве, то это действительно просто-просто сделайте ухо отсечения. Не волнуйтесь, это не O(n^2) для выпуклых многоугольников. Если вы сделаете это наивно (т. е. вы обрезаете уши, как вы их найдете), то вы получите треугольный вентилятор, который немного затягивает, если вы пытаетесь избежать осколков. Две тривиальные эвристики, которые могут улучшить триангуляцию, - это
- Сортировать уши, или, если это слишком медленно
- выберите ухо наугад.
Если вы хотите более надежный триангулятор на основе отсечения ушей, проверьте кулаком.
