Быстрый алгоритм вычисления процентилей для удаления выбросов
У меня есть программа, которая должна повторно вычислить приблизительный процентиль (статистику порядка) набора данных, чтобы удалить выбросы перед дальнейшей обработкой. В настоящее время я делаю это, сортируя массив значений и выбирая соответствующий элемент; это выполнимо, но это заметный всплеск на профилях, несмотря на то, что он является довольно незначительной частью программы.
Подробнее:
- набор данных содержит на заказе до 100000 плавающей запятой числа, и предполагается, что они" разумно " распределены - вряд ли будут дубликаты или огромные всплески плотности вблизи определенных значений; и если по какой-то странной причине распределение нечетное, это нормально для аппроксимации, чтобы быть менее точным, так как данные, вероятно, перепутались и дальнейшая обработка сомнительна. Однако данные не обязательно равномерно или нормально распределены; это просто очень маловероятно, чтобы быть вырожденным.
- приблизительное решение было бы хорошо, но я делаю надо понять как аппроксимация вводит ошибку, чтобы убедиться, что она действительна.
- поскольку целью является удаление выбросов, я вычисляю два процентиля по одним и тем же данным во все времена: например, один на 95% и один на 5%.
- приложение находится на C# с битами тяжелой работы на C++; псевдокод или ранее существовавшая библиотека в любом случае будет в порядке.
- совершенно другой способ удаления выбросов тоже был бы хорош, если это разумный.
- обновление: кажется, я ищу примерную алгоритм выбора.
хотя все это делается в цикле, данные (немного) отличаются каждый раз, поэтому нелегко повторно использовать структуру данных, как это было сделано на этот вопрос.
Решение
используя алгоритм выбора Википедии, предложенный Гронимом, уменьшил эту часть время выполнения Примерно в 20.
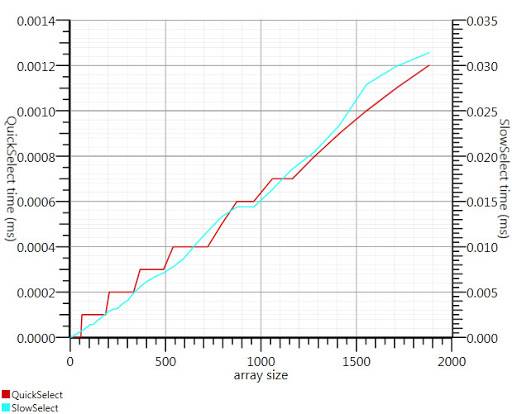
поскольку я не смог найти реализацию C#, вот что я придумал. Это быстрее даже для небольших входов, чем Array.Сортировка; и при 1000 элементах это в 25 раз быстрее.
public static double QuickSelect(double[] list, int k) {
return QuickSelect(list, k, 0, list.Length);
}
public static double QuickSelect(double[] list, int k, int startI, int endI) {
while (true) {
// Assume startI <= k < endI
int pivotI = (startI + endI) / 2; //arbitrary, but good if sorted
int splitI = partition(list, startI, endI, pivotI);
if (k < splitI)
endI = splitI;
else if (k > splitI)
startI = splitI + 1;
else //if (k == splitI)
return list[k];
}
//when this returns, all elements of list[i] <= list[k] iif i <= k
}
static int partition(double[] list, int startI, int endI, int pivotI) {
double pivotValue = list[pivotI];
list[pivotI] = list[startI];
list[startI] = pivotValue;
int storeI = startI + 1;//no need to store @ pivot item, it's good already.
//Invariant: startI < storeI <= endI
while (storeI < endI && list[storeI] <= pivotValue) ++storeI; //fast if sorted
//now storeI == endI || list[storeI] > pivotValue
//so elem @storeI is either irrelevant or too large.
for (int i = storeI + 1; i < endI; ++i)
if (list[i] <= pivotValue) {
list.swap_elems(i, storeI);
++storeI;
}
int newPivotI = storeI - 1;
list[startI] = list[newPivotI];
list[newPivotI] = pivotValue;
//now [startI, newPivotI] are <= to pivotValue && list[newPivotI] == pivotValue.
return newPivotI;
}
static void swap_elems(this double[] list, int i, int j) {
double tmp = list[i];
list[i] = list[j];
list[j] = tmp;
}
спасибо, Гроним, за то, что указал мне в правильном направлении!
10 ответов
решение гистограммы от Хенрика будет работать. Вы также можете использовать алгоритм выбора для эффективного поиска k самых больших или самых маленьких элементов в массиве из n элементов в O(n). Чтобы использовать это для 95-го процентиля, установите k=0.05 n и найдите k самых больших элементов.
ссылки:
http://en.wikipedia.org/wiki/Selection_algorithm#Selecting_k_smallest_or_largest_elements
вы можете оценить свои процентили только из части вашего набора данных, например, из первых нескольких тысяч точек.
на Glivenko–Кантелли теорема гарантирует, что это будет довольно хорошая оценка, если вы можете предположить, что ваши точки данных независимы.
Я использовал для идентификации выбросов, вычисляя стандартное отклонение. Все, что имеет расстояние более 2 (или 3) раз стандартное отклонение от среднего, является выбросом. 2 раза = около 95%.
поскольку вы вычисляете среднее значение, его также очень легко рассчитать стандартное отклонение очень быстро.
вы также можете использовать только подмножество данных для расчета цифры.
разделите интервал между минимумом и максимумом ваших данных на (скажем) 1000 ячеек и вычислите гистограмму. Затем постройте частичные суммы и посмотрите, где они сначала превышают 5000 или 95000.
есть несколько основных подходов, которые я могу думать. Во - первых, вычислить диапазон (найдя самые высокие и самые низкие значения), проецировать каждый элемент на процентиль ((x-min) / диапазон) и выбросить любой, который оценивается ниже .05 или выше .95.
второе-вычислить среднее и стандартное отклонение. Диапазон 2 стандартных отклонений от среднего (в обоих направлениях) будет заключать 95% нормально распределенного пространства выборки, что означает, что ваши выбросы будут в процентили 97.5. Вычисление среднего ряда является линейным, как и стандартный dev (квадратный корень из суммы разности каждого элемента и среднего). Затем вычтите 2 Сигмы из среднего и добавьте 2 Сигмы к среднему, и у вас есть свои пределы выбросов.
оба они будут вычисляться примерно в линейное время; первый требует двух проходов, второй занимает три (как только у вас есть свои пределы, вам все равно придется отбросить выбросы). Так как это операция на основе списка, я не думаю, что вы найдете что-либо с логарифмической или постоянной сложностью; любой дальнейший прирост производительности потребует либо оптимизации итерации и вычисления, либо введения ошибки путем выполнения вычислений на под-образце (например, каждый третий элемент).
хороший общий ответ на вашу проблему, кажется,RANSAC.
Учитывая модель и некоторые шумные данные, алгоритм эффективно восстанавливает параметры модели.
Вам нужно будет выбрать простую модель, которая может отображать ваши данные. Все гладкое должно быть в порядке. Скажем, смесь нескольких гауссов. RANSAC установит параметры вашей модели и оценит набор вкладышей одновременно. Затем выбросьте все, что не соответствует модели должным образом.
вы можете отфильтровать 2 или 3 стандартных отклонений, даже если данные не распределены нормально; по крайней мере, это будет сделано последовательно, что должно быть важно.
по мере удаления выбросов std dev изменится, вы можете сделать это в цикле, пока изменение std dev не будет минимальным. Хотите вы этого или нет, зависит от того, почему вы манипулируете данными таким образом. Некоторые статистики высказывают серьезные оговорки в отношении исключения выбросов. Но некоторые удаляют выбросы, чтобы доказать, что данные довольно нормально распределены.
не эксперт, но моя память подсказывает:
- чтобы точно определить процентильные точки, вам нужно отсортировать и подсчитать
- взятие выборки из данных и вычисление значений процентилей звучит как хороший план для достойного приближения, если вы можете получить хорошую выборку
- если нет, как предложил Хенрик, вы можете избежать полной сортировки, если вы делаете ведра и подсчитываете их
один набор данных из 100k элементов занимает почти нет времени для сортировки, поэтому я предполагаю, что вам придется делать это неоднократно. Если набор данных тот же набор, только немного обновлен, вам лучше всего построить дерево (O(N log N)), а затем удаление и добавление новых точек по мере их поступления (O(K log N) здесь K - количество измененных точек). В противном случае kth самый большой элемент решение уже упоминалось дает вам O(N) для каждого набора данных.
