Быстрый способ нормализации матрицы в MATLAB

Я хочу нормализовать каждый столбец матрицы в Matlab. Я пробовал две реализации:

Вариант A:

mx=max(x);
mn=min(x);
mmd=mx-mn;
for i=1:size(x,1)
    xn(i,:)=((x(i,:)-mn+(mmd==0))./(mmd+(mmd==0)*2))*2-1; 
end

Вариант B:

mn=mean(x);
sdx=std(x);
for i=1:size(x,1)
    xn(i,:)=(x(i,:)-mn)./(sdx+(sdx==0));
end

однако эти параметры занимают слишком много времени для моих данных, например 3-4 секунды на матрице 5000x53. Таким образом, есть ли лучшее решение?

9
matlab normalization performance

7 ответов

помните, что в MATLAB векторизация = скорость.

Если A является матрицей M x N,

A = rand(m,n);
minA = repmat(min(A), [size(A, 1), 1]);
normA = max(A) - min(A);               % this is a vector
normA = repmat(normA, [length(normA) 1]);  % this makes it a matrix
                                       % of the same size as A
normalizedA = (A - minA)./normA;  % your normalized matrix
8

использовать bsxfun вместо петли. Это может быть немного быстрее; однако, он также может использовать больше памяти (который может быть проблемой в вашем случае, если вы подкачки, все будет очень медленно).

чтобы нормализовать со средним и std, вы напишете

mn = mean(x);
sd = std(x);
sd(sd==0) = 1;

xn = bsxfun(@minus,x,mn);
xn = bsxfun(@rdivide,xn,sd);
15

примечание: Я не предоставляю новый ответ, но я сравниваю предлагаемые ответы.

Вариант A: Использование bsxfun()

function xn = normalizeBsxfun(x)

    mn = mean(x);
    sd = std(x);
    sd(sd==0) = eps;

    xn = bsxfun(@minus,x,mn);
    xn = bsxfun(@rdivide,xn,sd);

end

вариант B: использование for-loop

function xn = normalizeLoop(x)

    xn = zeros(size(x));

    for ii=1:size(x,2)
        xaux = x(:,ii);
        xn(:,ii) = (xaux - mean(xaux))./mean(xaux);
    end

end

мы сравниваем обе реализации для разных размеров матрицы:

expList = 2:0.5:5;
for ii=1:numel(expList)
    expNum = round(10^expList(ii));
    x = rand(expNum,expNum); 
    tic;
    xn = normalizeBsxfun(x);
    ts(ii) = toc; 
    tic;
    xn = normalizeLoop(x);
    tl(ii) = toc; 
end

figure;
hold on;
plot(round(10.^expList),ts,'b');
plot(round(10.^expList),tl,'r');
legend('bsxfun','loop');
set(gca,'YScale','log')

результаты показывают, что для малых матриц,bsxfun быстрее. Но, разница в пренебрежении способна для более высоких измерений, как это было также найдено в других в должности.

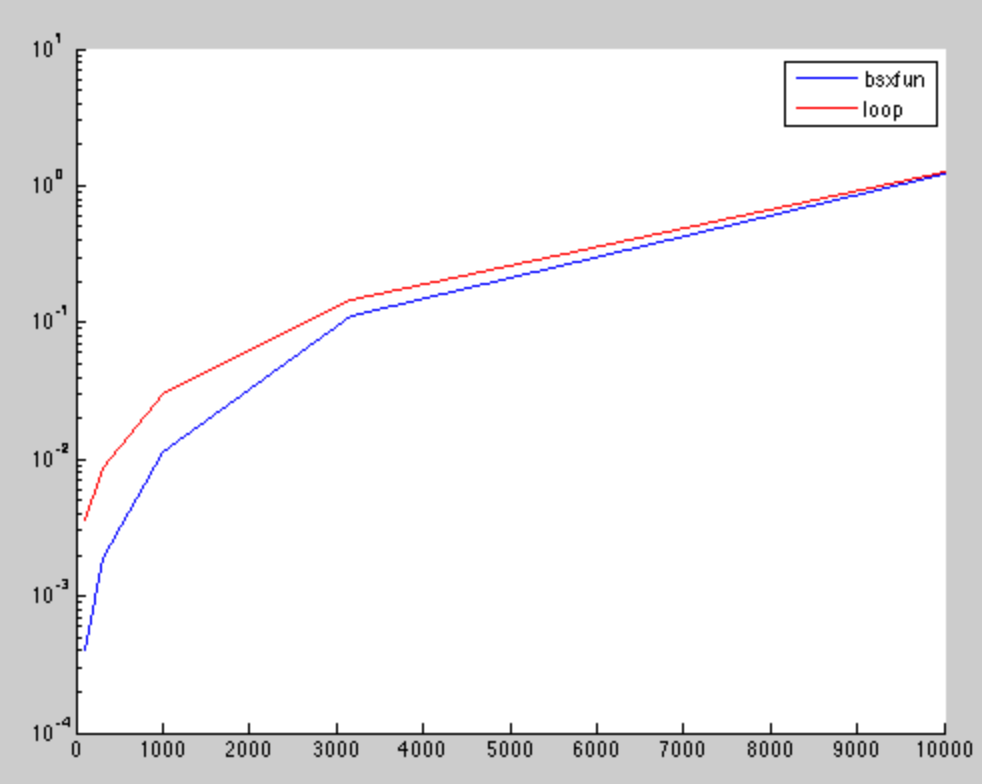
enter image description here

ось x-это квадратное корневое число элементов матрицы, а ось y-время вычисления в секундах.

3

пусть X быть m x n матрица и вы хотите нормализовать столбец мудрый.

следующий код matlab делает это

XMean = repmat(mean(X),m,1);
XStd = repmat(std(X),m,1);
X_norm = (X - XMean)./(XStd);

элемент мудрый ./ оператор объясняется здесь:http://www.mathworks.in/help/matlab/ref/arithmeticoperators.html

Примечание: Как упоминалось в op, это просто более быстрое решение и выполняет ту же задачу, что и цикл через матрицу. Базовая реализация этой встроенной функции делает его работать быстрее

3

Примечание: этот код работает в версиях Octave и MATLAB R2016b или выше.

function X_norm = normalizeMatrix(X)      
      mu = mean(X); %mean    
      sigma = std(X); %standard deviation   
      X_norm = (X - mu)./sigma;    
end
3

Как насчет использования

normc(X)

что бы нормализовать матрицу X columnwise. Однако вам нужно включить набор инструментов нейронной сети в свою установку.

1

Как насчет этого?

A = [7, 2, 6; 3, 8, 4]; % матрица 2x3

Asum = sum (A); % sum столбцы

Anorm = A. / Asum (единицы (размер (A, 1), 1), :); % нормализовать колонки

-3