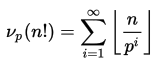Быстрый способ рассчитать n! mod m где m-простое число?
мне было любопытно, есть ли хороший способ сделать это. Мой текущий код что-то вроде:
def factorialMod(n, modulus):
ans=1
for i in range(1,n+1):
ans = ans * i % modulus
return ans % modulus
но это, кажется, довольно медленно!
Я также не могу вычислить n! а затем примените простой модуль, потому что иногда n настолько велико, что n! просто невозможно вычислить явно.
Я тоже наткнулся http://en.wikipedia.org/wiki/Stirling%27s_approximation и интересно, можно ли это вообще использовать здесь каким-то образом?
или, как я могу создать рекурсивную, memoized функцию в C++?
9 ответов
расширение моего комментария до ответа:
Да, есть более эффективные способы сделать это. но они очень грязные.
поэтому, если вам действительно не нужна дополнительная производительность, я не предлагаю пытаться реализовать их.
ключ должен отметить, что модуль (который по существу является делением) будет операцией узкого места. К счастью, есть очень быстрые алгоритмы, которые позволяют выполнить модуль над таким же числом много времен.
эти методы быстры, потому что они по существу устраняют модуль.
n может быть сколь угодно большим
Ну n не может быть угодно большой - если n >= m, потом n! ≡ 0 (mod m) (поскольку m является одним из факторов, по определению факториала).
предполагая, что n << m и вам нужен точно значение, ваш алгоритм не может получить быстрее, насколько мне известно. Однако, если n > m/2, вы можете использовать следующие личности (Уилсон теорема - Спасибо @Daniel Fischer!)
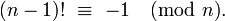
ограничить количество умножений примерно в m-n
(m-1)! ≡ -1 (mod m) 1 * 2 * 3 * ... * (n-1) * n * (n+1) * ... * (m-2) * (m-1) ≡ -1 (mod m) n! * (n+1) * ... * (m-2) * (m-1) ≡ -1 (mod m) n! ≡ -[(n+1) * ... * (m-2) * (m-1)]-1 (mod m)
это дает нам простой способ, чтобы вычислить n! (mod m) на m-n-1 умножений, плюс модульный инверсный:
def factorialMod(n, modulus):
ans=1
if n <= modulus//2:
#calculate the factorial normally (right argument of range() is exclusive)
for i in range(1,n+1):
ans = (ans * i) % modulus
else:
#Fancypants method for large n
for i in range(n+1,modulus):
ans = (ans * i) % modulus
ans = modinv(ans, modulus)
ans = -1*ans + modulus
return ans % modulus
мы можем перефразировать приведенное выше уравнение по-другому, что может или не может работать немного быстрее. Используя следующее личность:
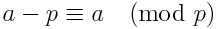
мы можем перефразировать уравнение как
n! ≡ -[(n+1) * ... * (m-2) * (m-1)]-1 (mod m)
n! ≡ -[(n+1-m) * ... * (m-2-m) * (m-1-m)]-1 (mod m)
(reverse order of terms)
n! ≡ -[(-1) * (-2) * ... * -(m-n-2) * -(m-n-1)]-1 (mod m)
n! ≡ -[(1) * (2) * ... * (m-n-2) * (m-n-1) * (-1)(m-n-1)]-1 (mod m)
n! ≡ [(m-n-1)!]-1 * (-1)(m-n) (mod m)
это может быть написано на Python следующим образом:
def factorialMod(n, modulus):
ans=1
if n <= modulus//2:
#calculate the factorial normally (right argument of range() is exclusive)
for i in range(1,n+1):
ans = (ans * i) % modulus
else:
#Fancypants method for large n
for i in range(1,modulus-n):
ans = (ans * i) % modulus
ans = modinv(ans, modulus)
#Since m is an odd-prime, (-1)^(m-n) = -1 if n is even, +1 if n is odd
if n % 2 == 0:
ans = -1*ans + modulus
return ans % modulus
Если вам не нужен точно значением, жизнь становится немного проще - вы можете использовать приближение Стирлинга для расчета приблизительного значения в O(log n) времени (через возведение в квадрат).
Наконец, Я следует отметить, что если это критично по времени и вы используете Python, попробуйте переключиться на C++. Исходя из личного опыта, вы должны ожидать увеличения скорости на порядок или больше, просто потому, что это именно тот тип связанного с процессором жесткого цикла, который изначально скомпилирован code превосходит at (кроме того, по какой-то причине GMP кажется гораздо более тонко настроенным, чем Bignum Python).
n! mod m можно вычислить в O (n1/2 + ε) операции вместо наивного O (n). Это требует использования полиномиального умножения FFT и стоит только для очень большого n, например n > 104.
контур алгоритма и некоторые тайминги можно увидеть здесь:http://fredrikj.net/blog/2012/03/factorials-mod-n-and-wilsons-theorem/
если мы хотим вычислить M = a*(a+1) * ... * (b-1) * b (mod p), мы можем использовать следующий подход, если предположим, что мы можем быстро добавлять, вычитать и умножать (mod p) и получить сложность времени выполнения O( sqrt(b-a) * polylog(b-a) ).
для простоты предположим,(b-a+1) = k^2, является квадратом. Теперь мы можем разделить наш продукт на k частей, т. е. M = [a*..*(a+k-1)] *...* [(b-k+1)*..*b]. Каждый из факторов в этом продукте имеет вид p(x)=x*..*(x+k-1), соответствующей x.
С помощью алгоритма быстрого умножения многочленов, таких как Schönhage–Штрассен, в divide & conquer образом, можно найти коэффициенты многочлена p(x) in O( k * polylog(k) ). Теперь, по-видимому, существует алгоритм замены k точек в той же степени-K полинома в O( k * polylog(k) ), что означает, что мы можем вычислить p(a), p(a+k), ..., p(b-k+1) быстро.
этот алгоритм подстановки многих точек в один многочлен описан в книге "простые числа" К. Померансом и Р. Крэндаллом. В конце концов, когда у вас есть эти k значения, вы можете умножить их в O(k) и получаем нужное значение.
обратите внимание, что все наши операции, где взят (mod p).
Точное время работы O(sqrt(b-a) * log(b-a)^2 * log(log(b-a))).
расширяя мой комментарий, это занимает около 50% времени для всех n в [100, 100007], где m=(117 | 1117):
Function facmod(n As Integer, m As Integer) As Integer
Dim f As Integer = 1
For i As Integer = 2 To n
f = f * i
If f > m Then
f = f Mod m
End If
Next
Return f
End Function
Если n = (m - 1) для простого m, то по http://en.wikipedia.org/wiki/Wilson ' s_theorem n! mod m = (m - 1)
также, как уже было указано! mod m = 0, если n > m
Я нашел эту следующую функцию на quora:
С f (n,m) = n! mod m;
function f(n,m:int64):int64;
begin
if n = 1 then f:= 1
else f:= ((n mod m)*(f(n-1,m) mod m)) mod m;
end;
вероятно, избили, используя трудоемкий цикл и умножение большого числа, хранящегося в строке. Кроме того, он применим к любому целому числу m.
Ссылку, где я нашел эту функцию : https://www.quora.com/How-do-you-calculate-n-mod-m-where-n-is-in-the-1000s-and-m-is-a-very-large-prime-number-eg-n-1000-m-10-9+7
этот алгоритм имеет O(n log log(n)) сложность времени предварительной обработки (из-за сита) и o(r(n)) сложность пространства, где r(n) - это простая функция подсчета. После предварительной обработки, запрос x! где x <= N is O(r(x) * log(x)).
к сожалению, это становится невозможным для 1010 так как r (1e9) составляет 455,052,511, для хранения простых чисел требуется почти 2 ГБ памяти. Для 109 однако, нам нужно было только около 300MB память.
предположим, что mod-1e9+7, чтобы избежать переполнения в C++, но это может быть что угодно.
способ вычисления N! mod m быстро
вычислить N! быстро, мы можем разложить N на его простые множители. Можно заметить, что если p-простой фактор N!, p должно быть Википедия там являются 50,847,534 примерно (~5 * 10^7) простыми числами меньше или равны 109. Это будет формула для использования:
vp (N!) наибольшее число такое, что pvp(N!) делит N!. формула Лежандра вычисляет vp(N!) в O (log (N)) времени. Вот формула из Википедии.
int factorial(int n) {
int ans = 1;
for (int i = 0; i < primes.size() && primes[i] <= n; i++) {
int e = 0;
for (int j = n; j > 0; ) {
j /= primes[i];
e += j;
}
ans = ((u64) ans * fast_power(primes[i], e)) % mod;
}
return ans;
}
fast_power(x, y) возвращает xy % mod в O (log (y)) время с помощью exponeniation по квадратуре.
Генерация Простых Чисел
я генерирую простые числа, используя решето Эратосфена. В моей реализации sieve я использую bitset для сохранения памяти. Моя реализация заняла 16-18seconds для генерации простых чисел до 10^9 когда я скомпилировано с -O3 флаг С процессор 2-го поколения i3. Я уверен, что есть лучшие алгоритмы/реализации для генерации простых чисел.
const int LIMIT = 1e9;
bitset<LIMIT+1> sieve;
vector<int> primes;
void go_sieve() {
primes.push_back(2);
int i = 3;
for (int i = 3; i * i <= LIMIT; i+=2) {
if (!sieve.test(i)) {
primes.push_back(i);
for (int j = i * i; j <= LIMIT; j += i) {
sieve.set(j);
}
}
}
while (i <= LIMIT) {
if (!sieve.test(i)) primes.push_back(i);
i+=2;
}
}
Потребление Памяти
по данным Википедия, есть 50,847,534 простых чисел, которые меньше или равны 10^9. Поскольку 32-разрядное целое число составляет 4 байта, простому вектору требуется 203,39 МБ (50,847,534 * 4 байта). Битсет сетки нуждается (125 МБ) 10^9 биты.
производительность
я смог вычислить 1,000,000,000! в 1.17 секунд после обработки.
Примечание: я сделал алгоритм с включенным флагом-O3.
предполагая, что оператор " mod " выбранной вами платформы достаточно быстр, вы ограничены в первую очередь скоростью, с которой вы можете вычислить n! и пространство, в котором вы можете его вычислить.
тогда это по существу 2-ступенчатая операция:
- вычислить n! (есть много быстрых алгоритмов, поэтому я не буду повторять здесь)
- возьмите мод результата
нет необходимости усложнять вещи, особенно если скорость-критический компонент. В общем, выполните как можно меньше операций внутри цикла.
Если вам нужно вычислить n! mod m несколько раз, затем вы можете захотеть запомнить значения, выходящие из функции, выполняющей вычисления. Как всегда, это классический компромисс пространства/времени, но таблицы поиска очень быстро.
наконец, вы можете объединить memoization с рекурсией (и батутами, если это необходимо), чтобы получить вещи действительно быстрый.