Catmull-ROM в Кривой без бугорков и без самопересечений
У меня есть следующий код для вычисления точек между четырьмя контрольными точками для создания кривой catmull-rom:
CGPoint interpolatedPosition(CGPoint p0, CGPoint p1, CGPoint p2, CGPoint p3, float t)
{
float t3 = t * t * t;
float t2 = t * t;
float f1 = -0.5 * t3 + t2 - 0.5 * t;
float f2 = 1.5 * t3 - 2.5 * t2 + 1.0;
float f3 = -1.5 * t3 + 2.0 * t2 + 0.5 * t;
float f4 = 0.5 * t3 - 0.5 * t2;
float x = p0.x * f1 + p1.x * f2 + p2.x * f3 + p3.x * f4;
float y = p0.y * f1 + p1.y * f2 + p2.y * f3 + p3.y * f4;
return CGPointMake(x, y);
}
это отлично работает, но я хочу создать то, что я думаю, называется центростремительной параметризацией. Это означает, что кривая будет иметь никаких бугорков и без самопересечений. Если я перемещаю одну контрольную точку очень близко к другой, кривая должна стать "меньше". Я прогуглил глаза, пытаясь найти способ сделать это. Кто-нибудь знает как это сделать это?
4 ответов
Мне нужно было реализовать это и для работы. Основная концепция, с которой вам нужно начать, заключается в том, что основное различие между обычной реализацией Catmull-Rom и модифицированными версиями заключается в том, как они обрабатывают время.
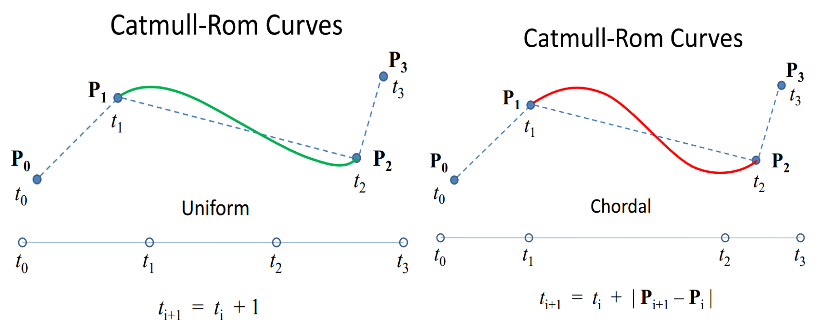
в непараметрированной версии из исходной реализации Catmull-Rom t начинается с 0 и заканчивается на 1 и вычисляет кривую от P1 до P2. В параметризованной реализации времени t начинается с 0 при P0 и сохраняет увеличение по всем четырем точкам. Таким образом, в однородном случае это будет 1 при P1 и 2 при P2, и вы передадите значения в диапазоне от 1 до 2 для своей интерполяции.
хордовый случай показывает |Pi+1-P / как изменение промежутка времени. Это просто означает, что вы можете использовать расстояние прямой линии между точками каждого сегмента для расчета фактической длины. Центростремительный случай просто использует немного другой метод для вычисления оптимального периода времени для каждого сегмент.
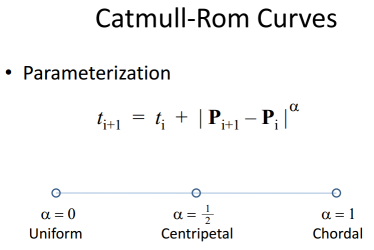
теперь нам просто нужно знать, как придумать уравнения, которые позволят нам подключить наши новые значения времени. Типичное уравнение Catmull-Rom имеет только один t в нем, время, за которое вы пытаетесь вычислить значение. Я нашел лучшую статью для описания того, как эти параметры вычисляются здесь:http://www.cemyuksel.com/research/catmullrom_param/catmullrom.pdf. Они были сосредоточены на математической оценке кривых, но в это важнейшая формула Барри и Голдмана.(1)
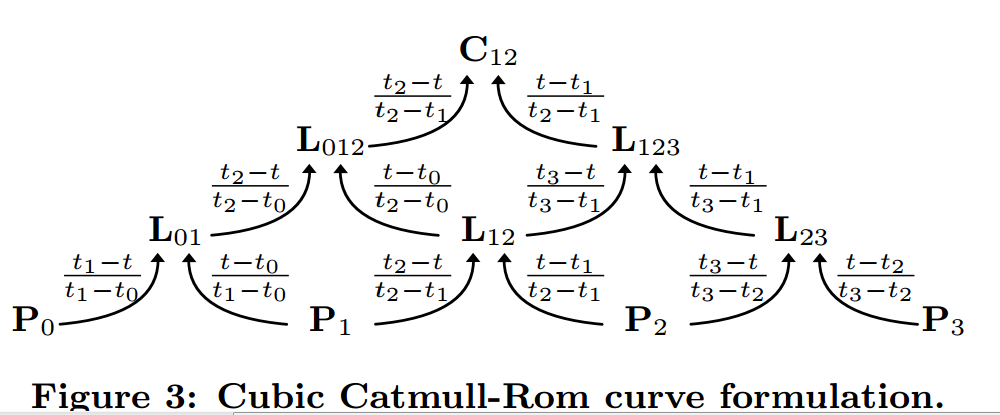
на диаграмме выше стрелки означают "умноженное на" отношение, указанное в Стрелке.
Это дает нам то, что нам нужно на самом деле выполнить расчет, чтобы получить желаемый результат. X и Y вычисляются независимо, хотя я использовал коэффициент "расстояние" для изменения времени на основе 2D-расстояния, а не 1D-расстояния.
существует гораздо более простой и эффективный способ реализовать это, который требует только вычисления касательных с использованием другой формулы, без необходимости реализации рекурсивного алгоритма оценки Барри и Голдмана.
Если вы возьмете параметризацию Барри-Голдмана (на которую ссылается ответ Теда) C (t) для узлов (t0, t1,t2, t3) и контрольных точек (P0,P1,P2,P3), ее замкнутая форма довольно сложна, но в конце концов это все еще кубический полином в t, когда вы ограничьте его интервалом (t1, t2). Поэтому все, что нам нужно для его полного описания, - это значения и касательные в двух конечных точках t1 и t2. Если мы разработаем эти значения (я сделал это в Mathematica), мы найдем
C(t1) = P1
C(t2) = P2
C'(t1) = (P1 - P0) / (t1 - t0) - (P2 - P0) / (t2 - t0) + (P2 - P1) / (t2 - t1)
C'(t2) = (P2 - P1) / (t2 - t1) - (P3 - P1) / (t3 - t1) + (P3 - P2) / (t3 - t2)
мы можем просто подключите его в стандартная формула для вычисления кубического сплайна с заданными значениями и касательными в конечных точках, и у нас есть наш неоднородный сплайн Catmull-Rom. Одно предостережение заключается в том,что вышеуказанные касательные вычисляются для интервала (t1, t2), поэтому если вы хотите оценить кривую в стандартном интервале (0,1), просто масштабируйте касательные, умножая их на коэффициент (t2-t1).
Я поставил рабочий пример C++ на Ideone:http://ideone.com/NoEbVM
Я также вставлю код ниже.
#include <iostream>
#include <cmath>
using namespace std;
struct CubicPoly
{
float c0, c1, c2, c3;
float eval(float t)
{
float t2 = t*t;
float t3 = t2 * t;
return c0 + c1*t + c2*t2 + c3*t3;
}
};
/*
* Compute coefficients for a cubic polynomial
* p(s) = c0 + c1*s + c2*s^2 + c3*s^3
* such that
* p(0) = x0, p(1) = x1
* and
* p'(0) = t0, p'(1) = t1.
*/
void InitCubicPoly(float x0, float x1, float t0, float t1, CubicPoly &p)
{
p.c0 = x0;
p.c1 = t0;
p.c2 = -3*x0 + 3*x1 - 2*t0 - t1;
p.c3 = 2*x0 - 2*x1 + t0 + t1;
}
// standard Catmull-Rom spline: interpolate between x1 and x2 with previous/following points x0/x3
// (we don't need this here, but it's for illustration)
void InitCatmullRom(float x0, float x1, float x2, float x3, CubicPoly &p)
{
// Catmull-Rom with tension 0.5
InitCubicPoly(x1, x2, 0.5f*(x2-x0), 0.5f*(x3-x1), p);
}
// compute coefficients for a nonuniform Catmull-Rom spline
void InitNonuniformCatmullRom(float x0, float x1, float x2, float x3, float dt0, float dt1, float dt2, CubicPoly &p)
{
// compute tangents when parameterized in [t1,t2]
float t1 = (x1 - x0) / dt0 - (x2 - x0) / (dt0 + dt1) + (x2 - x1) / dt1;
float t2 = (x2 - x1) / dt1 - (x3 - x1) / (dt1 + dt2) + (x3 - x2) / dt2;
// rescale tangents for parametrization in [0,1]
t1 *= dt1;
t2 *= dt1;
InitCubicPoly(x1, x2, t1, t2, p);
}
struct Vec2D
{
Vec2D(float _x, float _y) : x(_x), y(_y) {}
float x, y;
};
float VecDistSquared(const Vec2D& p, const Vec2D& q)
{
float dx = q.x - p.x;
float dy = q.y - p.y;
return dx*dx + dy*dy;
}
void InitCentripetalCR(const Vec2D& p0, const Vec2D& p1, const Vec2D& p2, const Vec2D& p3,
CubicPoly &px, CubicPoly &py)
{
float dt0 = powf(VecDistSquared(p0, p1), 0.25f);
float dt1 = powf(VecDistSquared(p1, p2), 0.25f);
float dt2 = powf(VecDistSquared(p2, p3), 0.25f);
// safety check for repeated points
if (dt1 < 1e-4f) dt1 = 1.0f;
if (dt0 < 1e-4f) dt0 = dt1;
if (dt2 < 1e-4f) dt2 = dt1;
InitNonuniformCatmullRom(p0.x, p1.x, p2.x, p3.x, dt0, dt1, dt2, px);
InitNonuniformCatmullRom(p0.y, p1.y, p2.y, p3.y, dt0, dt1, dt2, py);
}
int main()
{
Vec2D p0(0,0), p1(1,1), p2(1.1,1), p3(2,0);
CubicPoly px, py;
InitCentripetalCR(p0, p1, p2, p3, px, py);
for (int i = 0; i <= 10; ++i)
cout << px.eval(0.1f*i) << " " << py.eval(0.1f*i) << endl;
}
вот версия кода Ted для iOS. Я исключил части "z".
.h
typedef enum {
CatmullRomTypeUniform,
CatmullRomTypeChordal,
CatmullRomTypeCentripetal
} CatmullRomType ;
.м
-(NSMutableArray *)interpolate:(NSArray *)coordinates withPointsPerSegment:(NSInteger)pointsPerSegment andType:(CatmullRomType)curveType {
NSMutableArray *vertices = [[NSMutableArray alloc] initWithArray:coordinates copyItems:YES];
if (pointsPerSegment < 3)
return vertices;
//start point
CGPoint pt1 = [vertices[0] CGPointValue];
CGPoint pt2 = [vertices[1] CGPointValue];
double dx = pt2.x - pt1.x;
double dy = pt2.y - pt1.y;
double x1 = pt1.x - dx;
double y1 = pt1.y - dy;
CGPoint start = CGPointMake(x1*.5, y1);
//end point
pt2 = [vertices[vertices.count-1] CGPointValue];
pt1 = [vertices[vertices.count-2] CGPointValue];
dx = pt2.x - pt1.x;
dy = pt2.y - pt1.y;
x1 = pt2.x + dx;
y1 = pt2.y + dy;
CGPoint end = CGPointMake(x1, y1);
[vertices insertObject:[NSValue valueWithCGPoint:start] atIndex:0];
[vertices addObject:[NSValue valueWithCGPoint:end]];
NSMutableArray *result = [[NSMutableArray alloc] init];
for (int i = 0; i < vertices.count - 3; i++) {
NSMutableArray *points = [self interpolate:vertices forIndex:i withPointsPerSegment:pointsPerSegment andType:curveType];
if ([points count] > 0)
[points removeObjectAtIndex:0];
[result addObjectsFromArray:points];
}
return result;
}
-(double)interpolate:(double*)p time:(double*)time t:(double) t {
double L01 = p[0] * (time[1] - t) / (time[1] - time[0]) + p[1] * (t - time[0]) / (time[1] - time[0]);
double L12 = p[1] * (time[2] - t) / (time[2] - time[1]) + p[2] * (t - time[1]) / (time[2] - time[1]);
double L23 = p[2] * (time[3] - t) / (time[3] - time[2]) + p[3] * (t - time[2]) / (time[3] - time[2]);
double L012 = L01 * (time[2] - t) / (time[2] - time[0]) + L12 * (t - time[0]) / (time[2] - time[0]);
double L123 = L12 * (time[3] - t) / (time[3] - time[1]) + L23 * (t - time[1]) / (time[3] - time[1]);
double C12 = L012 * (time[2] - t) / (time[2] - time[1]) + L123 * (t - time[1]) / (time[2] - time[1]);
return C12;
}
-(NSMutableArray*)interpolate:(NSArray *)points forIndex:(NSInteger)index withPointsPerSegment:(NSInteger)pointsPerSegment andType:(CatmullRomType)curveType {
NSMutableArray *result = [[NSMutableArray alloc] init];
double x[4];
double y[4];
double time[4];
for (int i=0; i < 4; i++) {
x[i] = [points[index+i] CGPointValue].x;
y[i] = [points[index+i] CGPointValue].y;
time[i] = i;
}
double tstart = 1;
double tend = 2;
if (curveType != CatmullRomTypeUniform) {
double total = 0;
for (int i=1; i < 4; i++) {
double dx = x[i] - x[i-1];
double dy = y[i] - y[i-1];
if (curveType == CatmullRomTypeCentripetal) {
total += pow(dx * dx + dy * dy, 0.25);
}
else {
total += pow(dx * dx + dy * dy, 0.5); //sqrt
}
time[i] = total;
}
tstart = time[1];
tend = time[2];
}
int segments = pointsPerSegment - 1;
[result addObject:points[index+1]];
for (int i =1; i < segments; i++) {
double xi = [self interpolate:x time:time t:tstart + (i * (tend - tstart)) / segments];
double yi = [self interpolate:y time:time t:tstart + (i * (tend - tstart)) / segments];
NSLog(@"(%f,%f)",xi,yi);
[result addObject:[NSValue valueWithCGPoint:CGPointMake(xi, yi)]];
}
[result addObject:points[index+2]];
return result;
}
кроме того, вот метод превращения массива точек в путь Безье для рисования, используя выше
-(UIBezierPath*)bezierPathFromPoints:(NSArray *)points withGranulaity:(NSInteger)granularity
{
UIBezierPath __block *path = [[UIBezierPath alloc] init];
NSMutableArray *curve = [self interpolate:points withPointsPerSegment:granularity andType:CatmullRomTypeCentripetal];
CGPoint __block p0 = [curve[0] CGPointValue];
[path moveToPoint:p0];
//use this loop to draw lines between all points
for (int idx=1; idx < [curve count]; idx+=1) {
CGPoint c1 = [curve[idx] CGPointValue];
[path addLineToPoint:c1];
};
//or use this loop to use actual control points (less smooth but probably faster)
// for (int idx=0; idx < [curve count]-3; idx+=3) {
// CGPoint c1 = [curve[idx+1] CGPointValue];
// CGPoint c2 = [curve[idx+2] CGPointValue];
// CGPoint p1 = [curve[idx+3] CGPointValue];
//
// [path addCurveToPoint:p1 controlPoint1:c1 controlPoint2:c2];
// };
return path;
}
Я написала что-то на Питоне (в адаптированном виде Catmull-ROM в Википедии страницы), который сравнивает униформа, centripedal, и chordial ЧР сплайнов (хотя вы можете установить альфа как угодно), используя случайные данные (вы можете использовать свои собственные данные и функции работают отлично). Обратите внимание, что для конечных точек я просто застрял в быстром "взломе", который поддерживает наклон от первой и последних 2 точек, хотя расстояние между этой точкой и первой/потерянной известной точкой произвольно (я установил его на 1% от домен... без всякой причины. Поэтому имейте это в виду, прежде чем обращаться к чему-то важному):
# coding: utf-8
# In[1]:
import numpy
import matplotlib.pyplot as plt
get_ipython().magic(u'pylab inline')
# In[2]:
def CatmullRomSpline(P0, P1, P2, P3, a, nPoints=100):
"""
P0, P1, P2, and P3 should be (x,y) point pairs that define the Catmull-Rom spline.
nPoints is the number of points to include in this curve segment.
"""
# Convert the points to numpy so that we can do array multiplication
P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])
# Calculate t0 to t4
alpha = a
def tj(ti, Pi, Pj):
xi, yi = Pi
xj, yj = Pj
return ( ( (xj-xi)**2 + (yj-yi)**2 )**0.5 )**alpha + ti
t0 = 0
t1 = tj(t0, P0, P1)
t2 = tj(t1, P1, P2)
t3 = tj(t2, P2, P3)
# Only calculate points between P1 and P2
t = numpy.linspace(t1,t2,nPoints)
# Reshape so that we can multiply by the points P0 to P3
# and get a point for each value of t.
t = t.reshape(len(t),1)
A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1
A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2
A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3
B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2
B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3
C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2
return C
def CatmullRomChain(P,alpha):
"""
Calculate Catmull Rom for a chain of points and return the combined curve.
"""
sz = len(P)
# The curve C will contain an array of (x,y) points.
C = []
for i in range(sz-3):
c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3],alpha)
C.extend(c)
return C
# In[8]:
# Define a set of points for curve to go through
Points = numpy.random.rand(12,2)
x1=Points[0][0]
x2=Points[1][0]
y1=Points[0][1]
y2=Points[1][1]
x3=Points[-2][0]
x4=Points[-1][0]
y3=Points[-2][1]
y4=Points[-1][1]
dom=max(Points[:,0])-min(Points[:,0])
rng=max(Points[:,1])-min(Points[:,1])
prex=x1+sign(x1-x2)*dom*0.01
prey=(y1-y2)/(x1-x2)*dom*0.01+y1
endx=x4+sign(x4-x3)*dom*0.01
endy=(y4-y3)/(x4-x3)*dom*0.01+y4
print len(Points)
Points=list(Points)
Points.insert(0,array([prex,prey]))
Points.append(array([endx,endy]))
print len(Points)
# In[9]:
#Define alpha
a=0.
# Calculate the Catmull-Rom splines through the points
c = CatmullRomChain(Points,a)
# Convert the Catmull-Rom curve points into x and y arrays and plot
x,y = zip(*c)
plt.plot(x,y,c='green',zorder=10)
# Plot the control points
px, py = zip(*Points)
plt.plot(px,py,'or')
a=0.5
c = CatmullRomChain(Points,a)
x,y = zip(*c)
plt.plot(x,y,c='blue')
a=1.
c = CatmullRomChain(Points,a)
x,y = zip(*c)
plt.plot(x,y,c='red')
plt.grid(b=True)
plt.show()
# In[10]:
Points
# In[ ]:
исходный код:https://en.wikipedia.org/wiki/Centripetal_Catmull%E2%80%93Rom_spline
