Что именно представляет собой Big not notation?

сначала давайте поймем, что такое big O, big Theta и big Omega. Они все наборы функций.

Big O дает верхний асимптотическая граница, в то время как большая Омега дает нижнюю границу. Большая тета дает обоим.

все это Ө(f(n)) тоже O(f(n)), но не наоборот.
T(n) находится в Ө(f(n)) Если это и в O(f(n)) и Omega(f(n)).
в комплекте терминологии, Ө(f(n)) is the пересечение of O(f(n)) и Omega(f(n))

например, худший случай сортировки слияния-это оба O(n*log(n)) и Omega(n*log(n)) - и таким образом также Ө(n*log(n)), а также O(n^2) С n^2 асимптотически "больше", чем он. Однако, это не Ө(n^2), так как алгоритм не Omega(n^2).

немного более глубокое математическое объяснение

O(n) является асимптотической верхней границей. Если T(n) и O(f(n)), это означает, что от некоего n0 постоянно C такое, что T(n) <= C * f(n). С другой стороны, большая Омега говорит, что существует постоянная C2 такое, что T(n) >= C2 * f(n))).

не путай!

не путать с худшим, лучшим и средним анализом случаев: все три (Omega, O, Theta) обозначения не связанные с лучшими, худшими и средними случаями анализа алгоритмов. Каждый из них может быть применен к каждому анализу.

мы обычно используют его для анализа сложности алгоритмов (как пример сортировки слиянием выше). Когда мы говорим: "алгоритм-это O(f(n))", что мы действительно имеем в виду, это " сложность алгоритмов при худшем¹ анализ случая O(f(n)) "- значение-масштабируется "аналогично" (или формально, не хуже) функции f(n).

почему мы заботимся об асимптотической границе алгоритма?

Ну, есть много причин для этого, но я считаю, самое главное них:

1. гораздо труднее определить точно функция сложности, таким образом, мы "компрометируем" на нотациях big-O/big-Theta, которые достаточно информативны теоретически.
2. точное количество операций также зависит от платформы. Например, если у нас есть вектор (список) из 16 цифр. Сколько это займет операций? Ответ: это зависит. Некоторые процессоры позволяют векторные дополнения, в то время как другие нет, поэтому ответ варьируется между различные реализации и разные машины, что является нежелательным свойством. Однако нотация big-O гораздо более постоянна между машинами и реализациями.

чтобы продемонстрировать эту проблему, посмотрите на следующие графики:

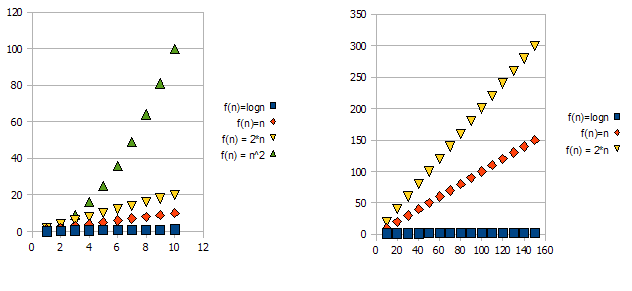
понятно, что f(n) = 2*n "хуже", чем f(n) = n. Но разница не так велика, как от другой функции. Мы видим это f(n)=logn быстро получать гораздо ниже чем другое функции и f(n) = n^2 быстро становится намного выше, чем другие.
So-из-за вышеуказанных причин мы "игнорируем" постоянные факторы (2* в примере графиков) и берем только обозначение big-O.

в приведенном выше примере f(n)=n, f(n)=2*n обоих в O(n) и Omega(n) - и таким образом также будет в Theta(n).
с другой стороны - f(n)=logn будет O(n) (это "лучше", чем f(n)=n), но не будет Omega(n) - и таким образом тоже не будет в Theta(n).
симметрично, f(n)=n^2 будет Omega(n), но не O(n), а значит - тоже не Theta(n).

¹обычно, хотя и не всегда. когда класс анализа (худший, средний и лучший) отсутствует, мы действительно имеем в виду худшем случае.

чтобы ответить на ваш вопрос, асимптотическая нотация и функции в асимптотической нотации также должны быть объяснены. Если у вас есть терпение, чтобы прочитать все это, все будет очень понятно в конце.

1. Асимптотическая нотация

думать об алгоритмах вы можете использовать 2 основные идеи:

1. определите, сколько времени занимает алгоритм с точки зрения его ввода.
2. фокус на как быстро функция растет с размером входного сигнала; ака темп роста хода время. Пример: предположим, что алгоритм, работающий на входе размера n, принимает 6N^2 + 100n + 300 машинных инструкций. Член 6n^2 становится больше остальных членов, 100 n + 300, как только n становится достаточно большим, в этом случае 20.

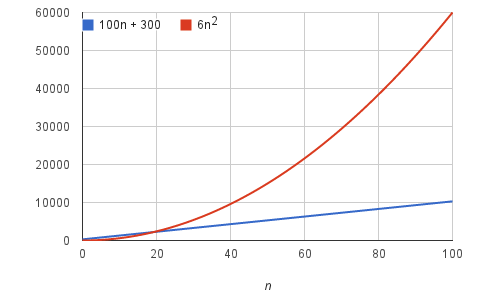
мы бы сказали, что время работы этого алгоритма растет как n^2, отбрасывая коэффициент 6 и остальные члены 100n + 300. На самом деле не имеет значения, какие коэффициенты мы используем; пока работает времениn^2 + bn + c, для некоторых чисел a > 0, b и c всегда будет значение n, для которого an^2 больше, чем bn + c, и эта разница увеличивается по мере увеличения n. Отбросив постоянные коэффициенты и менее значимые члены, мы используем асимптотическую нотацию.

2. Большая Тета!--4-->

вот простая реализация линейного поиска

var doLinearSearch = function(array) {
  for (var guess = 0; guess < array.length; guess++) {
    if (array[guess] === targetValue) { 
        return guess;  // found it!
    }
  }
  return -1;  // didn't find it
};

• каждый из этих вычислений требует постоянного количество времени при каждом выполнении. Если цикл for повторяется n раз, то время для всех n итераций равно c1 * n, где c1-сумма времен для вычислений в одной итерации цикла. Этот код имеет немного дополнительных накладных расходов для настройки for-loop (включая инициализацию guess до 0) и, возможно, возвращает -1 в конце. Назовем время для этой накладной c2, которая также является константой. Таким образом, общее время линейного поиска в худшем случае С1*Н+С2.
• постоянный фактор c1 и термин низкого порядка c2 не говорят нам о темпе роста времени выполнения. Важно то, что наихудшее время выполнения линейного поиска растет как размер массива n. Обозначение, которое мы используем для этого времени работы, - Θ (n). Это греческая буква "тета", и мы говорим" большая тета Н "или просто"тета Н".--9-->

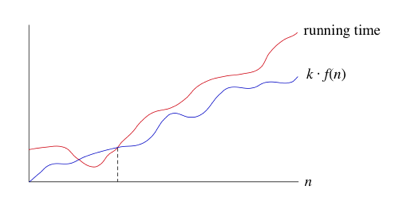
• когда мы говорим, что определенное время работы Θ (n), мы говорим, что как только n становится большим достаточно, что время работы составляет не менее k1*n и не более k2 * n для некоторых констант k1 и k2. Вот как думать о Θ (n)

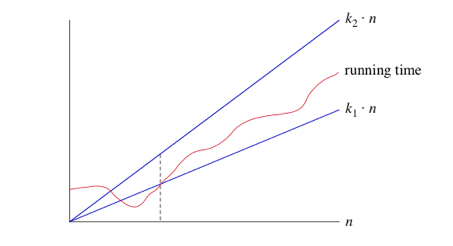
• для малых значений n нам все равно, как время работы сравнивается с k1*n или k2*n. Но как только n становится достаточно большим-На или справа от пунктирной линии-время работы должно быть зажато между k1*n и k2*n. Пока эти константы k1 и k2 существуют, мы говорим, что время выполнения Θ (n).

• когда мы используем большую-not нотацию, мы говорим, что имеем асимптотически туго связан на время работы. "Асимптотически", потому что это имеет значение только для больших значений n. "крепко связаны" потому что мы прибили время работы в пределах постоянного фактора выше и ниже.

3. Функции в асимптотической нотации

• предположим, что алгоритм постоянное количество времени, независимо от размер входного сигнала. Например, если вам дали массив, который уже отсортирован в порядке возрастания, и вам нужно было найти минимальный элемент, это займет постоянное время, так как минимальный элемент должен быть в индексе 0. Поскольку нам нравится использовать функцию n в асимптотической нотации, можно сказать, что этот алгоритм работает в Θ(n^0) времени. Почему? Потому что n^0 = 1, а время работы алгоритма находится в пределах некоторого постоянного коэффициента 1. На практике мы не пишем Θ (n^0), однако; мы пишем Θ(1)
• вот список функций в асимптотической нотации, с которыми мы часто сталкиваемся при анализе алгоритмов, перечисленных от самого медленного до самого быстрорастущего. Этот список не является исчерпывающим; есть много алгоритмов, время работы которых здесь не отображается:
• Θ (1) (он же постоянный поиск)
• Θ (lg n) (он же двоичный поиск)
• Θ (n) (он же линейный поиск)
• Θ (n*lg n)
• Θ (n^2)
• Θ(n^2 * lg n)
• Θ (n^3)

• Θ (2^n)

• обратите внимание, что экспоненциальная функция a^n, где a > 1, растет быстрее, чем любая полиномиальная функция n^b, где b-любая константа.

4. Big-O notation

• мы используем большую-not нотацию, чтобы асимптотически связать рост времени работы с постоянными факторами выше и ниже. Иногда мы хотим прыгнуть только сверху. Было бы удобно иметь форма асимптотической нотации, которая означает, что " время работы растет не более этого, но оно может расти медленнее.- Мы используем обозначение "Биг-О" как раз для таких случаев.
• если время выполнения O(f(n)), то для достаточно большого n время выполнения не более k*f (n) для некоторой постоянной k. Вот как думать о времени выполнения, которое O (f(n)):
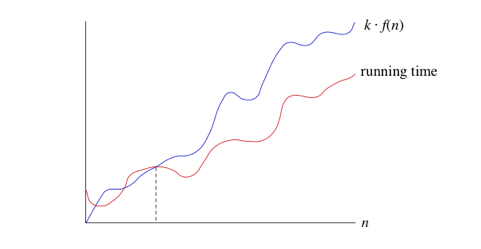
• если вы вернетесь к определению обозначения big-Θ, вы заметите, что оно очень похоже на обозначение big-O, за исключением того, что большая-not нотация ограничивает бег как сверху, так и снизу, а не только сверху. Если мы говорим, что время выполнения Θ(f(n)) в конкретной ситуации, то это также O(f(n)). Например, мы можем сказать, что, поскольку наихудшее время работы двоичного поиска-Θ(lg n), это также O (lg n). Обратное не обязательно верно: как мы видели, мы можем сказать, что двоичный поиск всегда выполняется в o(lg n) времени, но не то, что он всегда работает в Θ(lg n) времени.
• Предположим, у вас есть 10 долларов в кармане. Вы подходите к своему другу и говорите: "у меня в кармане есть деньги, и я гарантирую, что это не более миллиона долларов.- Ваше утверждение абсолютно верно, хотя и не слишком точно. Миллион долларов-это верхняя граница 10 долларов, так же как O(n) - верхняя граница времени выполнения двоичного поиска.
• другие, неточные, верхние границы двоичного поиска будут O(n^2), O(n^3) и O (2^n). Но никто из Θ(N) и Θ(п^2),Θ(П^3), andΘ(2^н​​) было бы правильно описать время работы бинарного поиска в любом случае.

5. Big-Ω (Big-Omega) обозначение

• иногда мы хотим сказать, что алгоритм занимает по крайней мере определенное количество времени, не обеспечивая верхнюю границу. Мы используем обозначение big-Ω; это греческая буква "omega"."
• если время выполнения Ω (f(n)), то для достаточно большого n, время выполнения по крайней мере k*f (n) для некоторой константы k. Вот как думать о беге время, которое Ω (f (n)):
• мы говорим, что время работы "большое-Ω f(n)."Мы используем нотацию big-Ω для асимптотических нижних границ, поскольку она ограничивает рост времени выполнения снизу для достаточно больших входных размеров.
• так же, как Θ(f(n)) автоматически подразумевает O(f(n)), оно также автоматически подразумевает Ω(f(n)). Таким образом, мы можем сказать, что наихудшее время выполнения двоичного поиска-Ω(lg n). Мы также можем делать правильные, но неточные утверждения, используя big-Ω нотация. Например, как если бы у вас действительно был миллион долларов в кармане, вы можете честно сказать: "у меня есть сумма денег в кармане, и это по крайней мере 10 долларов", вы также можете сказать, что наихудшее время работы бинарного поиска-Ω(1), потому что это занимает по крайней мере постоянное время.

ссылка: https://www.khanacademy.org

тета (n): функция f(n) принадлежит Theta(g(n)), если существуют положительные константы c1 и c2 такое, что f(n) можно зажать между c1(g(n)) и c2(g(n)). Я. e он дает как верхнюю, так и нижнюю границу.

Theta(g (n)) = { f (n): существуют положительные константы c1, c2 и n1 такие, что 0=n1 }

когда мы говорим f(n)=c2(g(n)) или f(n)=c1(g(n)) он представляет асимптотически плотно связаны.

O (n): он дает только верхнюю границу (может быть или не быть туго)

O (g (n)) = {f(n): существуют положительные константы c и n1 такие, что 0=n1}

ex: связанный 2*(n^2) = O(n^2) асимптотически плотно, тогда как граница 2*n = O(n^2) не является асимптотически плотным.

o (n): это дает только верхнюю границу (никогда не плотную границу)

заметная разница между O (n) & o (n) f (n) меньше, чем cg(n) для всех n>=n1, но не равно, как в O (n).

ex: 2*n = o(n^2), а 2*(n^2) != o(n^2)