Что использовать для создания flow free-like Game random level?
Мне нужен совет. Я разрабатываю игру, похожую на Flow Free, в которой игровая доска состоит из сетки и цветных точек, и пользователь должен соединить одинаковые цветные точки вместе, не перекрывая другие линии, и использовать все свободные места на доске.
мой вопрос о создании уровня. Я хочу, чтобы уровни генерировались случайным образом (и должны, по крайней мере, быть в состоянии решить себя, чтобы он мог дать игрокам подсказки), и я в тупике относительно того, какой алгоритм использовать. Есть предложения?
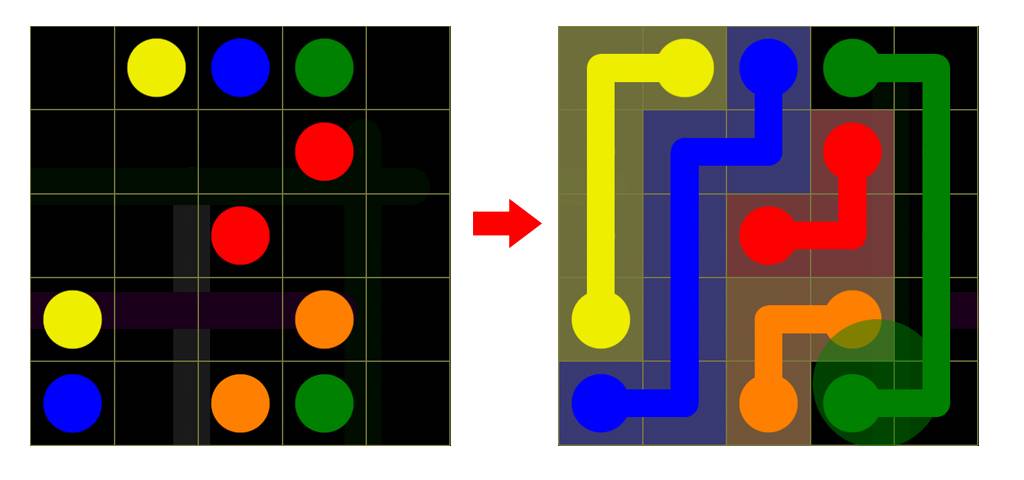
Примечание: изображение показывает цель Flow Free, и это та же цель, что я разрабатываю.
Спасибо за помощь. :)
5 ответов
рассмотрите возможность решения вашей проблемы с помощью пары более простых, более управляемых алгоритмов: один алгоритм, который надежно создает простые, предварительно решенные платы, а другой, который перестраивает потоки, чтобы сделать простые платы более сложными.
первая часть, построение простой предварительно решенной платы, тривиальна (если вы хотите, чтобы это было), если вы используете n потоки на nxn решетки:
- для каждого потока...
- поместите головную точку в верхней части первая открытая колонка.
- поместите хвостовую точку в нижней части этого столбца.
кроме того, вы можете предоставить свои собственные ручные стартовые платы для перехода ко второй части. Единственная цель этого этапа-получить действительную доску, даже если она просто тривиальна или предопределена, поэтому стоит сохранить ее простой.
вторая часть, переставляя потоки, включает в себя петлю над каждым потоком, видя, какой из них может работать с его соседний поток расти и сжиматься:
- для некоторого количества итераций...
- выберите случайный поток
f. - если
fимеет минимальную длину (скажем, 3 квадрата), перейдите к следующей итерации, потому что мы не можем сжатьfпрямо сейчас. - если головная точка
f- это рядом с точкой из другого потокаg(если более одногоgна выбор, наугад)...- движение
f's голова точка один квадрат вдоль его потока (т. е. пройдите его один квадрат к хвосту).fТеперь на один квадрат короче, и есть пустой квадрат. (Загадка теперь не решена.) - переместить соседнюю точку из
gна пустую площадь, освобожденнуюf. Теперь есть пустой квадрат, гдеgточка переместилась. - заполните это пустое место потоком из
g. Теперьgна один квадрат длиннее, чем в начале этой итерации. (Головоломка возвращается к тоже решается.)
- движение
- повторите предыдущий шаг для
f's хвост точка.
- выберите случайный поток
подход в его нынешнем виде ограничен (точки всегда будут соседями), но его легко расширить:
- добавить шаг к петле через тело потока
f, ищу хитрых способов подкачки с других потоков... - добавить шаг, который предотвращает перемещение точки в старый местоположение...
- добавить любые другие идеи, которые вы придумали.
общее решение здесь, вероятно, меньше, чем идеальное, к которому вы стремитесь, но теперь у вас есть два простых алгоритма, которые вы можете конкретизировать дальше, чтобы служить роли одного большого, всеобъемлющего алгоритма. В конце концов, я думаю, что этот подход управляемый, а не загадочный, и его легко настроить, и, если ничего другого, хорошее место для начала.
обновление: Я закодировал доказательство концепции, основанное на шагах выше. Начиная с первой сетки 5x5 ниже, процесс произвел последующие 5 различных плат. Некоторые из них интересны, некоторые нет, но они всегда действительны с одним известным решением.
Точка Отсчета
5 Случайных Результатов (извините за криво скриншоты)




и случайный 8x8 для хорошей меры. Этот отправной точкой был такой же простой подход, как и выше.
самый простой способ создать такой уровень-найти способ его решения. Таким образом, вы можете создать любую случайную начальную конфигурацию и определить, является ли она допустимым уровнем, пытаясь ее решить. Это породит самые разнообразные уровни.
и даже если вы найдете способ генерировать уровни каким-то другим способом, вы все равно захотите применить этот алгоритм решения, чтобы доказать, что сгенерированный уровень хорош ;)
грубой силы перечисление
если плата имеет размер ячеек NxN, а также доступно N цветов, грубая сила, перечисляющая все возможные конфигурации (независимо от того, формируют ли они фактические пути между начальными и конечными узлами), будет принимать:
- N^2 ячейки всего
- 2n ячеек, уже занятых начальными и конечными узлами
- N^2 - 2n ячеек, для которых цвет еще не определен
- N цветов доступный.
- N^(N^2 - 2N) возможные комбинации.
и
- для N=5 это означает 5^15 = 30517578125 комбинаций.
- для N=6 это означает 6^24 = 4738381338321616896 комбинаций.
другими словами, количество возможных комбинаций довольно велико для начала, но также растет смехотворно быстро, как только вы начинаете делать доску больше.
ограничение количества ячеек на цвет
очевидно, мы должны попытаться уменьшить количество конфигураций как можно больше. Один из способов сделать это - рассмотреть минимальное расстояние ("dMin") между начальной и конечной ячейками каждого цвета-мы знаем, что должно быть по крайней мере столько ячеек с этим цветом. Вычисление минимального расстояния может быть сделано с помощью простого заливки или алгоритма Дейкстры. (N. B. обратите внимание, что весь следующий раздел обсуждает только клеток, но не говорит что-нибудь об их мест)
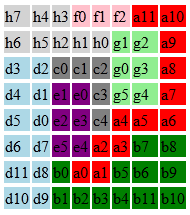
в вашем примере это означает (не считая начальной и конечной ячеек)
dMin(orange) = 1
dMin(red) = 1
dMin(green) = 5
dMin(yellow) = 3
dMin(blue) = 5
это означает, что из 15 клеток, для которых цвет еще не определен, должно быть не менее 1 оранжевой, 1 красной, 5 зеленой, 3 желтой и 5 синей клеток, что также составляет в общей сложности 15 клеток. Для этого конкретного примера это означает, что соединение начальной и конечной ячеек каждого цвета (одним из) кратчайших путей заполняет всю доску - т. е. после заполнения доски кратчайшими путями не остается неокрашенных ячеек. (Это следует считать "удачей", не каждая начальная конфигурация платы приведет к этому).
обычно после этого шага у нас есть несколько ячеек, которые могут быть свободно окрашены, назовем это число U. Для N=5,
U = 15 - (dMin(orange) + dMin(red) + dMin(green) + dMin(yellow) + dMin(blue))
поскольку эти ячейки могут принимать любой цвет, мы также можем определить максимальное количество ячеек, которые могут иметь определенный цвет:
dMax(orange) = dMin(orange) + U
dMax(red) = dMin(red) + U
dMax(green) = dMin(green) + U
dMax(yellow) = dMin(yellow) + U
dMax(blue) = dMin(blue) + U
(в этом конкретном примере U=0, поэтому минимальное количество ячеек на цвет также является максимальным).
поиск пути с использованием ограничений расстояния
если бы мы должны были грубой силой перечислить все возможные комбинации, используя эти ограничения цвета, у нас было бы намного меньше комбинаций, о которых нужно беспокоиться. Более конкретно, в этом конкретном примере мы бы имели:
15! / (1! * 1! * 5! * 3! * 5!)
= 1307674368000 / 86400
= 15135120 combinations left, about a factor 2000 less.
однако, это еще не дает нам собственно пути. поэтому лучше было бы вернуться к поиску, где мы обрабатываем каждый цвет по очереди и пытаемся найти все пути, которые:
- не пересекает уже окрашенную ячейку
- не короче dMin(цвет) и не длиннее dMax (цвет).
второй критерий уменьшит количество путей, сообщаемых на цвет, что приводит к тому, что общее количество путей будет значительно уменьшено (из-за комбинаторного эффект.)
в псевдо-код:
function SolveLevel(initialBoard of size NxN)
{
foreach(colour on initialBoard)
{
Find startCell(colour) and endCell(colour)
minDistance(colour) = Length(ShortestPath(initialBoard, startCell(colour), endCell(colour)))
}
//Determine the number of uncoloured cells remaining after all shortest paths have been applied.
U = N^(N^2 - 2N) - (Sum of all minDistances)
firstColour = GetFirstColour(initialBoard)
ExplorePathsForColour(
initialBoard,
firstColour,
startCell(firstColour),
endCell(firstColour),
minDistance(firstColour),
U)
}
}
function ExplorePathsForColour(board, colour, startCell, endCell, minDistance, nrOfUncolouredCells)
{
maxDistance = minDistance + nrOfUncolouredCells
paths = FindAllPaths(board, colour, startCell, endCell, minDistance, maxDistance)
foreach(path in paths)
{
//Render all cells in 'path' on a copy of the board
boardCopy = Copy(board)
boardCopy = ApplyPath(boardCopy, path)
uRemaining = nrOfUncolouredCells - (Length(path) - minDistance)
//Recursively explore all paths for the next colour.
nextColour = NextColour(board, colour)
if(nextColour exists)
{
ExplorePathsForColour(
boardCopy,
nextColour,
startCell(nextColour),
endCell(nextColour),
minDistance(nextColour),
uRemaining)
}
else
{
//No more colours remaining to draw
if(uRemaining == 0)
{
//No more uncoloured cells remaining
Report boardCopy as a result
}
}
}
}
FindAllPaths
это только оставляет FindAllPaths (доска, цвет, startCell, endCell, minDistance, maxDistance) для реализации. Хитрость здесь в том, что мы ищем не самые короткие пути, а любой пути, которые попадают в диапазон, определяемый minDistance и maxDistance. Следовательно, мы не можем просто использовать Дейкстры или a*, потому что они будут записывать только кратчайший путь к каждой ячейке, а не любой возможные объезды.
один из способов найти эти пути - использовать многомерный массив для платы, где каждая ячейка способна хранить несколько путевых точек, а путевая точка определяется как пара (предыдущая путевая точка, расстояние до начала координат). Предыдущая путевая точка необходима, чтобы иметь возможность восстановить весь путь, как только мы достигли места назначения, и расстояние до начала предотвращает нас от превышения maxDistance.
поиск всех путей может быть выполнен используя заливку, как исследование от startCell наружу, где для данной ячейки каждый неокрашенный или такой же, как текущий цветной сосед рекурсивно исследуется (за исключением тех, которые формируют наш текущий путь к началу), пока мы не достигнем либо endCell, либо превысим maxDistance.
улучшение этой стратегии заключается в том, что мы не исследуем от startCell наружу до endCell, но что мы исследуем от startCell и endCell наружу параллельно, используя Пол (maxDistance / 2) и Ceil(maxDistance / 2) как соответствующие максимальные расстояния. Для больших значений maxDistance это должно уменьшить количество исследованных ячеек с 2 * maxDistance^2 до maxDistance^2.
я реализовал следующий алгоритм в my numberlink решатель и генератор. В enforces правило, что путь никогда не может коснуться себя, что нормально в большинстве "хардкор" numberlink приложений и головоломок
- сначала доска выложена домино 2x1 простым, детерминированным способом. Если это невозможно (на бумаге нечетной области), нижний правый угол ушел как одиночка.
- затем домино случайным образом перемешиваются путем вращения случайные пары соседей. Это не делается в случае ширины или высоты, равной 1.
- теперь, в случае бумаги нечетной области, нижний правый угол прикреплен к одно из соседних домино. Это всегда будет возможно.
- наконец, мы можем начать находить случайные пути через домино, комбинируя их когда мы проезжаем. Особое внимание уделяется не подключать "потоки neighboour" что создало бы головоломки, которые "удваивают себя".
- перед пазл напечатан мы "компактные" диапазон цветов, как можно больше.
- головоломка печатается путем замены всех позиций, которые не являются потоковыми головками с a .
мой формат numberlink использует символы ascii вместо чисел. Вот пример:
$ bin/numberlink --generate=35x20
Warning: Including non-standard characters in puzzle
35 20
....bcd.......efg...i......i......j
.kka........l....hm.n....n.o.......
.b...q..q...l..r.....h.....t..uvvu.
....w.....d.e..xx....m.yy..t.......
..z.w.A....A....r.s....BB.....p....
.D.........E.F..F.G...H.........IC.
.z.D...JKL.......g....G..N.j.......
P...a....L.QQ.RR...N....s.....S.T..
U........K......V...............T..
WW...X.......Z0..M.................
1....X...23..Z0..........M....44...
5.......Y..Y....6.........C.......p
5...P...2..3..6..VH.......O.S..99.I
........E.!!......o...."....O..$$.%
.U..&&..J.\.(.)......8...*.......+
..1.......,..-...(/:.."...;;.%+....
..c<<.==........)./..8>>.*.?......@
.[..[....]........:..........?..^..
..._.._.f...,......-.`..`.7.^......
{{......].....|....|....7.......@..
и здесь я запускаю его через мой решатель (то же семя):
$ bin/numberlink --generate=35x20 | bin/numberlink --tubes
Found a solution!
┌──┐bcd───┐┌──efg┌─┐i──────i┌─────j
│kka│└───┐││l┌─┘│hm│n────n┌o│┌────┐
│b──┘q──q│││l│┌r└┐│└─h┌──┐│t││uvvu│
└──┐w┌───┘d└e││xx│└──m│yy││t││└──┘│
┌─z│w│A────A┌┘└─r│s───┘BB││┌┘└p┌─┐│
│D┐└┐│┌────E│F──F│G──┐H┐┌┘││┌──┘IC│
└z└D│││JKL┌─┘┌──┐g┌─┐└G││N│j│┌─┐└┐│
P──┐a││││L│QQ│RR└┐│N└──┘s││┌┘│S│T││
U─┐│┌┘││└K└─┐└─┐V││└─────┘││┌┘││T││
WW│││X││┌──┐│Z0││M│┌──────┘││┌┘└┐││
1┐│││X│││23││Z0│└┐││┌────M┌┘││44│││
5│││└┐││Y││Y│┌─┘6││││┌───┐C┌┘│┌─┘│p
5││└P│││2┘└3││6─┘VH│││┌─┐│O┘S┘│99└I
┌┘│┌─┘││E┐!!│└───┐o┘│││"│└─┐O─┘$$┌%
│U┘│&&│└J│\│(┐)┐└──┘│8││┌*└┐┌───┘+
└─1└─┐└──┘,┐│-└┐│(/:┌┘"┘││;;│%+───┘
┌─c<<│==┌─┐││└┐│)│/││8>>│*┌?│┌───┐@
│[──[└─┐│]││└┐│└─┘:┘│└──┘┌┘┌┘?┌─^││
└─┐_──_│f││└,│└────-│`──`│7┘^─┘┌─┘│
{{└────┘]┘└──┘|────|└───7└─────┘@─┘
Я тестировал замену шага (4) функцией, которая итеративно случайным образом объединяет два соседних пути. Однако это игра гораздо плотнее головоломки, и я уже думаю, что выше почти слишком плотный, чтобы быть трудным.
вот список проблем, которые я создал разного размера:https://github.com/thomasahle/numberlink/blob/master/puzzles/inputs3
Я думаю, вы захотите сделать это в два шага. Шаг 1) Найдите набор непересекающихся путей, которые соединяют все ваши точки, затем 2) вырастите/сдвиньте эти пути, чтобы заполнить всю доску
мои мысли на Шаге 1 должны по существу выполнять алгоритм Dijkstra как на всех точках одновременно, растя вместе пути. Подобно Dijkstra, я думаю, вы захотите заполнить каждую из своих точек, выбирая, какой узел искать дальше, используя некоторую эвристику (моя интуиция говорит, что выбор точки с наименьшими степенями свободы сначала, затем на расстоянии, могут быть хорошими). Очень отличается от Dijkstra, хотя я думаю, что мы могли бы застрять с тем, чтобы вернуться, когда у нас есть несколько путей, пытающихся вырасти в один узел. (Это, конечно, может быть довольно проблематично на больших картах, но не может быть большой проблемой на небольших картах, таких как у вас выше.)
вы также можете решить для некоторых из более простых путей, прежде чем начать вышеуказанный алгоритм, в основном, чтобы сократить о количестве необходимых обратных путей. В частности, если вы можете сделать трассировку между точками вдоль края доски, вы можете гарантировать, что соединение этих двух точек таким образом никогда не будет мешать другим путям, поэтому вы можете просто заполнить их и вывести этих парней из уравнения. Затем вы можете продолжить итерацию, пока все эти" быстрые и легкие " пути не будут найдены путем трассировки вдоль границ платы или границ существующих путей. Этот алгоритм на самом деле полностью решить приведенный выше пример платы, но, несомненно, потерпит неудачу в другом месте .. тем не менее, это было бы очень дешево выполнить и сократить время поиска для предыдущего алгоритма.
кроме того
вы можете просто сделать реальный алгоритм Дейкстры между каждым набором точек, сначала вычеркивая ближайшие точки (или пробуя их в некоторых случайных порядках несколько раз). Это, вероятно, будет работать для значительного числа случаев, и когда это не удастся просто выбросьте карту и создайте новую.
как только вы решите Шаг 1, Шаг 2 должен быть проще, хотя и не обязательно тривиальным. Чтобы вырастить свои пути, я думаю, вы захотите вырастить свои пути наружу (поэтому сначала пути, ближайшие к стенам, растут к стенам, затем другие внутренние пути наружу и т. д.). Чтобы расти, я думаю, у вас будет две основные операции, переворачивая углы и расширяясь в соседние пары пустых квадратов.. то есть, если у вас есть линия как
.v<<.
v<...
v....
v....
сначала вы хотите перевернуть углы, чтобы заполнить свои краевые пространства
v<<<.
v....
v....
v....
тогда вы захотите расшириться в соседние пары открытого пространства
v<<v.
v.^<.
v....
v....
v<<v.
>v^<.
v<...
v....
etc..
обратите внимание, что то, что я изложил, не гарантирует решение, если оно существует, но я думаю, что вы сможете найти его большую часть времени, если он существует, а затем в случаях, когда карта не имеет решения или алгоритм не может его найти, просто выбросьте карту и попробуйте другой:)
У вас есть два варианта:
- написать собственный решатель
- грубая сила.
Я использовал опцию (2) для создания плат типа Boggle, и это очень успешно. Если вы идете с опцией (2), Вот как вы это делаете:
инструменты:
- напишите a * решатель.
- написать случайный создатель доски
решение:
- генерация случайной платы, состоящей только из конечные точки
- пока доска не решена:
- получите две ближайшие друг к другу конечные точки, которые еще не решены
- запустите* для создания пути
- обновить доску, чтобы следующий* знает новый макет платы с новым путем, отмеченным как не проходимый.
- при выходе из цикла проверьте успех / сбой (используется вся плата/etc) и запустите снова, если это необходимо
A* на 10x10 должен работать в сотых долях секунды. Вы, наверное, можете решить 1к+ советов/секунду. Так что 10 секунд бега должна сделать вам несколько пригодных советов.
бонусные баллы:
- при создании уровней для пакета уровней IAP (в покупке приложения) не забудьте проверить зеркала/вращения/отражения/и т. д., чтобы у вас не было одной платы копии другой (которая просто хромает).
- придумайте метрику, которая выяснит, являются ли две доски "похожими", и если да, выбросьте одну из них.
