Convolve2d просто с помощью Numpy

Я изучаю обработку изображений с помощью Numpy и сталкиваюсь с проблемой фильтрации с сверткой.

Я хотел бы свернуть изображение в сером масштабе. (сверните 2d-массив с меньшим 2d-массивом)

у кого-нибудь есть идея уточнение мой метод ?

Я знаю, что scipy поддерживает convolve2d, но я хочу сделать convolve2d только с помощью Numpy.

что я сделал

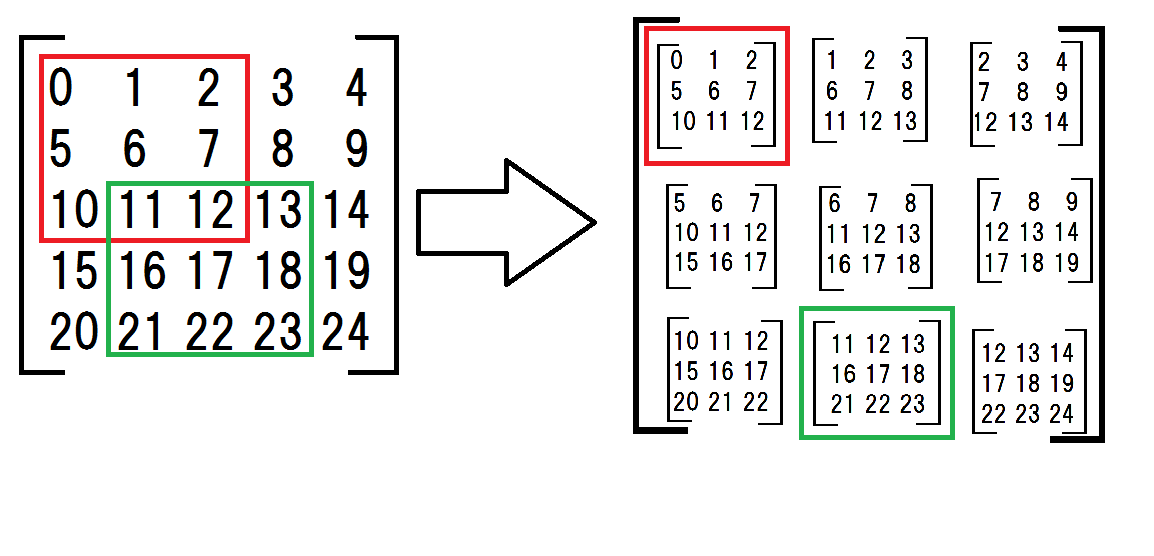
первый, Я сделал 2d-массив подматриц.

a = np.arange(25).reshape(5,5) # original matrix

submatrices = np.array([
     [a[:-2,:-2], a[:-2,1:-1], a[:-2,2:]],
     [a[1:-1,:-2], a[1:-1,1:-1], a[1:-1,2:]],
     [a[2:,:-2], a[2:,1:-1], a[2:,2:]]])

подматрицы кажутся сложными, но то, что я делаю, показано на следующем рисунке.

submatrices

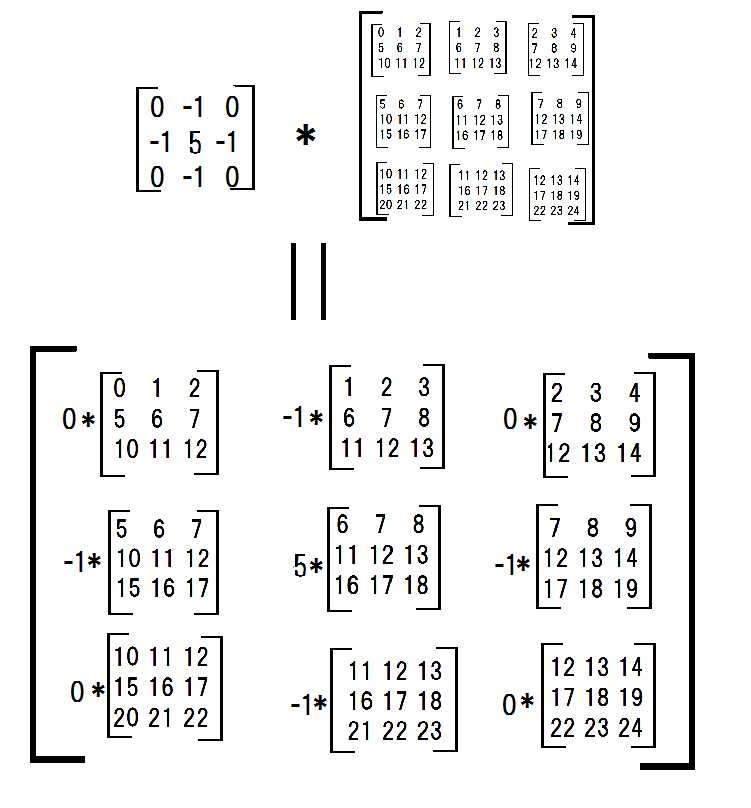
затем я умножил каждую подматрицу с помощью фильтра.

conv_filter = np.array([[0,-1,0],[-1,4,-1],[0,-1,0]])
multiplied_subs = np.einsum('ij,ijkl->ijkl',conv_filter,submatrices)

multiplied_subs

и подвел их.

np.sum(np.sum(multiplied_subs, axis = -3), axis = -3)
#array([[ 6,  7,  8],
#       [11, 12, 13],
#       [16, 17, 18]])

таким образом, этот procudure можно назвать моей convolve2d.

def my_convolve2d(a, conv_filter):
    submatrices = np.array([
         [a[:-2,:-2], a[:-2,1:-1], a[:-2,2:]],
         [a[1:-1,:-2], a[1:-1,1:-1], a[1:-1,2:]],
         [a[2:,:-2], a[2:,1:-1], a[2:,2:]]])
    multiplied_subs = np.einsum('ij,ijkl->ijkl',conv_filter,submatrices)
    return np.sum(np.sum(multiplied_subs, axis = -3), axis = -3)

однако, я нахожу это my_convolve2d хлопотно по 3 причинам.

  1. генерация подматриц слишком неудобна, что трудно читать и может использоваться только тогда, когда фильтр 3*3
  2. размер вариантных подматриц кажется слишком большим, так как он примерно на 9 складок больше исходной матрицы.
  3. суммирование, кажется, немного не понятный. Проще говоря, некрасиво.

Спасибо, что прочитали это далеко.

вид обновления. Я написал conv3d для себя. Я оставлю это как общественное достояние.

def convolve3d(img, kernel):
    # calc the size of the array of submatracies
    sub_shape = tuple(np.subtract(img.shape, kernel.shape) + 1)

    # alias for the function
    strd = np.lib.stride_tricks.as_strided

    # make an array of submatracies
    submatrices = strd(img,kernel.shape + sub_shape,img.strides * 2)

    # sum the submatraces and kernel
    convolved_matrix = np.einsum('hij,hijklm->klm', kernel, submatrices)

    return convolved_matrix
6
convolution image-processing matrix numpy python

3 ответов

вы можете создать подмассивы с помощью as_strided [1]:

import numpy as np

a = np.array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19],
       [20, 21, 22, 23, 24]])

sub_shape = (3,3)
view_shape = tuple(np.subtract(a.shape, sub_shape) + 1) + sub_shape
strides = a.strides + a.strides

sub_matrices = np.lib.stride_tricks.as_strided(a,view_shape,strides)

чтобы избавиться от второй "уродливой" суммы, измените свой einsum Так что выходной массив имеет только j и k. Это подразумевает ваше второе суммирование.

conv_filter = np.array([[0,-1,0],[-1,5,-1],[0,-1,0]])
m = np.einsum('ij,ijkl->kl',conv_filter,sub_matrices)

# [[ 6  7  8]
#  [11 12 13]
#  [16 17 18]]
9

очищены с помощью as_strided и @Crispin ' s einsum трюк сверху. Вводит размер фильтра в расширенную форму. Следует даже разрешить неквадратные входы, если индексы совместимы.

def conv2d(a, f):
    s = f.shape + tuple(np.subtract(a.shape, f.shape) + 1)
    strd = numpy.lib.stride_tricks.as_strided
    subM = strd(a, shape = s, strides = a.strides * 2)
    return np.einsum('ij,ijkl->kl', f, subM)
2

вы также можете использовать fft (один из более быстрых методов для выполнения свертки)

from numpy.fft import fft2, ifft2
import numpy as np

def fft_convolve2d(x,y):
    """ 2D convolution, using FFT"""
    fr = fft2(x)
    fr2 = fft2(np.flipud(np.fliplr(y)))
    m,n = fr.shape
    cc = np.real(ifft2(fr*fr2))
    cc = np.roll(cc, -m/2+1,axis=0)
    cc = np.roll(cc, -n/2+1,axis=1)
    return cc
  • https://gist.github.com/thearn/5424195
  • вы должны поместить фильтр в тот же размер, что и изображение (поместите его в середину мата zeros_like.)

ура, Дэн!--2-->

2