Эффективное получение изометрических позиций сетки в ограничительной рамке
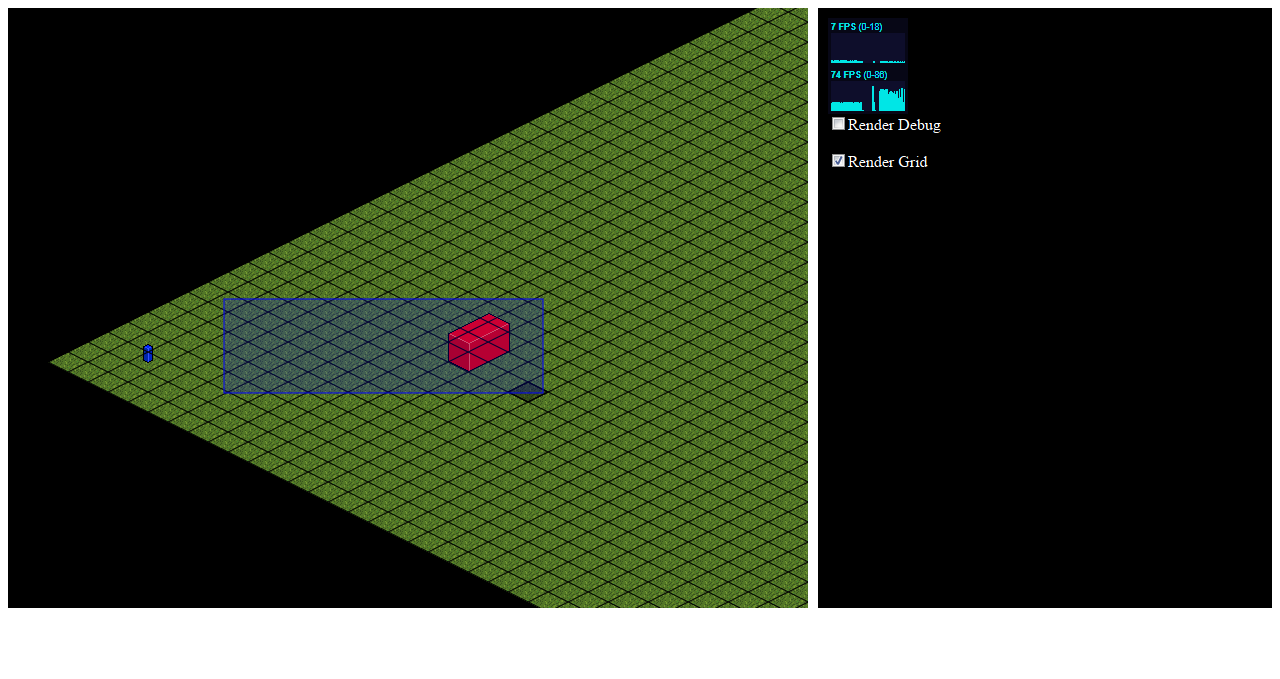
У меня изометрической сетки системы, который координирует с [0,0] в левом углу сетки (угол на рисунке выше) с X приращение к нижней части изображения и y увеличивая к верху (так [0, высота] будет в верхнем углу и [ширина, 0] будет в нижнем углу в виде ромба с ширина и высота-размер сетки, т. е.. 200 х 200 квадратов)
в любом случае, мне нужна помощь в получении массив изометрических позиций сетки, которые содержатся в синем поле, показанном на изображении. За исключением итерации по каждому экрану x,y и получения соответствующей позиции сетки (см. Этот вопрос, который я задал ранее о том, как преобразовать из позиции экрана в позитон сетки получить строку/столбец на изометрической сетке.) Я не уверен, как этого достичь эффективно.
был вопрос, который я нашел ранее, который почти точно такой же Ссылка здесь. в ответ состоял в том, чтобы отобразить сетку на изображение с разными цветами для каждого квадрата сетки, а затем определить, какие цвета присутствовали под квадратом, я реализовал это решение, но это довольно медленно! Я почти думаю, что проверка положения сетки для каждого пикселя в поле выбора будет быстрее. Почему javascript так медленен в цикле!
Мне действительно нужно математическое решение этой проблемы на основе моей системы координат, но я не могу придумать что-то, что работает (и обрабатывает поле выбора, выходящее из сетки)
пожалуйста, дайте мне знать, если вам нужна дополнительная информация.
Edit: к сожалению, поставляемые ответы не работали до сих пор, так как выбор похож на алмазную выбранную область на квадратной сетке, на самом деле нет верхнего левого, нижнего правого угла для итерации, если я не пропустил точку ответов? Я оптимизировал подход рендеринга, но при большом выборе он по-прежнему добавляет заметное падение кадров как он проходит через все пиксельные проверки цвета и получает соответствующий квадрат
6 ответов
линейная алгебра-ответ. Здесь интересны две системы координат: экранные координаты и изометрические координаты. Преобразование углов выбранной области из координат экрана в изометрические координаты очень поможет вам.
пусть тета-угол между осями x и y изометрических координат, измеренный на экране, а единица-длина пикселя одного шага в изометрических координатах. Тогда
var c = Math.cos(theta/2);
var s = Math.sin(theta/2);
var origin = [oX, oY]; //the pixel coordinates of (0, 0)
var unit = 20;
var iso2Screen = function(iso) {
var screenX = origin[0] + unit * (iso[0] * c + iso[1] * c);
var screenY = origin[1] + unit * (iso[0] * -s + iso[1] * s);
return [screenX, screenY];
}
Инвертирование этого отношения, мы получаем
var screen2Iso = function(screen) {
var isoX = ((screen[0] - origin[0]) / c - (screen[1] - origin[1]) / s) / unit;
var isoY = ((screen[0] - origin[0]) / c + (screen[1] - origin[1]) / s) / unit;
теперь преобразуйте координаты экрана каждого угла окна выбора в изометрические координаты и получите минимальные и максимальные x и y.
var cornersScreen = ...//4-element array of 2-element arrays
var cornersIso = [];
for(var i = 0; i < 4; i++) {
cornersIso.push(screen2Iso(cornersScreen[i]));
}
var minX, maxX, minY, maxY;
minX = Math.min(cornersIso[0][0], cornersIso[1][0], cornersIso[2][0], cornersIso[3][0]);
maxX = Math.max(cornersIso[0][0], cornersIso[1][0], cornersIso[2][0], cornersIso[3][0]);
minY = Math.min(cornersIso[0][1], cornersIso[1][1], cornersIso[2][1], cornersIso[3][1]);
maxY = Math.max(cornersIso[0][1], cornersIso[1][1], cornersIso[2][1], cornersIso[3][1]);
все выбранные изометрические точки лежат внутри изометрического поля [minX, maxX] x [minY, maxY], но не все точки в этом поле находятся внутри выделения.
вы могли бы сделать много разных вещей, чтобы отсеять очков в этой коробке, что не в выборе, я бы предложите перебрать целочисленные значения изометрических x и y, преобразовать изометрические координаты в экранные координаты, а затем проверить, находится ли эта экранная координата в поле выбора, а именно:
var sMinX, sMaxX, sMinY, sMaxY;
sMinX = Math.min(cornersScreen[0][0], cornersScreen[1][0], cornersScreen[2][0], cornersScreen[3][0]);
sMaxX = Math.max(cornersScreen[0][0], cornersScreen[1][0], cornersScreen[2][0], cornersScreen[3][0]);
sMinY = Math.min(cornersScreen[0][1], cornersScreen[1][1], cornersScreen[2][1], cornersScreen[3][1]);
sMaxY = Math.max(cornersScreen[0][1], cornersScreen[1][1], cornersScreen[2][1], cornersScreen[3][1]);
var selectedPoints = [];
for(var x = Math.floor(minX); x <= Math.ceil(maxX); x++) {
for(var y = Math.floor(minY); x <= Math.ceil(maxY); y++) {
var iso = [x,y];
var screen = iso2Screen(iso);
if(screen[0] >= sMinX && screen[0] <= sMaxX && screen[1] >= sMinY && screen[1] <= sMaxY) {
selectedPoints.push(iso);
}
}
}
Я студент, делающий XNA игры для хобби. Я работаю над классической 2D-игрой на основе квадратов ( Проект В Квадрате). Ваша игра напомнила мне о моей работе, поэтому я решил помочь вам.
Я думаю, что это должно быть сделано с использованием математики, а не графики, как вы упомянули.
сначала вы должны знать, какой квадрат (позиция на сетке) находится в начале "синего ящика" (возможно, поле выбора) и в конце выбора. Так что теперь ты знаешь начало и конец своего ... список.
поскольку в вашей игре квадраты, вероятно, имеют статический размер (или вы масштабируете камеру, но никогда не увеличиваете ширину/высоту), вы можете легко вычислить, какие квадраты находятся в поле выбора.
теперь вы знаете, что ваши квадраты перемещены на 45° r/l.
(Я говорю о XNA, как coordsys-up слева 0,0)
If ( selectedStartSquare.selectionY <= square.height )
startY = selectedStartSquare.selectionY
else startY = selectedStartSquare.selectionY + 1;
if (selectedEndSquare.selectionY > square.height)
endY = -||-.selectionY
else endY = -||- + 1;
это даст вам начальные и конечные индексы высоты квадратов. То же самое нужно сделать для Х индексов.
теперь у вас есть все вам нужно получить все квадраты. Пройдите через X из selectedStartSquare.X в endX и корыто Y с циклом for от selectedStartSquare.Y для endY, но изменить начало каждый раз ( startYIndex++ каждый цикл)
Это просто близкий пример, так как я никогда не работал с изометрической игры. Это, вероятно, потребуется некоторая настройка, но я " думаю!!- это должно сработать. (Написал это перед сном и даже без бумаги, так как я уже был в постели... удачи)
извините за мой английский, я из Хорватия так...
Я думаю, у Александра есть очень хорошая идея о том, как решить вашу проблему.
вот альтернатива:
простой способ уменьшить количество квадратов сетки для проверки-найти координаты углов синего поля в координатах сетки.
В вашем примере вам нужно будет только проверить квадраты, где 1<x<13 and 3<y<16.
Альваро дает короткий и краткий ответ на как проверить, находится ли точка внутри коробки.
учитывая регулярную компоновку плиток, вы не можете просто начать с верхнего левого угла селектора, hittest, чтобы найти, какая плитка, а затем перейти к следующей плитке в соответствии с тем, как они расположены.
например, если ваши плитки 32x16, вы должны начать с угла и двигаться вдоль 32, а затем, когда вы достигнете конца, перейдите по следующей строке.
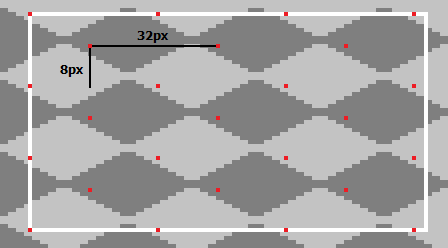
например, в странном псевдокоде...
var altRow = false;
var selectedTiles = [];
for (int y = selectorBox.top; y < selectorBox.top+selectorBox.height; y+=TILE_HEIGHT/2) {
for (int x = selectorBox.left ; x < selectorBox.left+selectorBox.width; x+= TILE_WIDTH) {
selectedTiles.add(tileAtPoint(x + (altRow ? - TILE_WIDTH/2 : 0), y);
}
altRow = !altRow;
}
мой подход, который я не видел, чтобы кто-то еще делал: 1. Преобразуйте выбранный прямоугольник в сетку (получите положение плитки каждого из углов) 2. Теперь у нас есть 2d-задача: найти все точки внутри преобразованного ромба.
Это можно сделать с помощью аналогичного: http://en.wikipedia.org/wiki/Flood_fill
но, может быть, что-то вроде этого лучше:
1. Start at the topmost
2. Go down
3. Go right until we encounter the edge (can be calculated from the rombus line)
4. Do the same thing but go left.
5. Go to 2 until we are at the middle
6. Go right and down.
7. Go right until we encouter the edge
8. Go left and down.
9. Go left until we encouter the edge
10. Go to 6 until we are at the bottom
на каждой плитке, которую мы посещаем, мы добавляем эту.
теперь единственная оставшаяся проблема-определить, столкнулись ли мы с ребром...
Я предполагаю, что вы можете получить координаты углов поля выбора, сопоставленных квадратам сетки iso. Это дает вам задачу построения графика с простым алгебраическим тестом для решения. Если мы начнем с углов в iso-квадратах (x1,y1) и (x2,y2), мы знаем, что нам нужно протестировать вдоль линий с наклоном 1 и -1, которые проходят через эти точки,
Итак, четыре строки: y-y1=x-x1, y-y1=x1-x,y-y2=x-x2,y-y2=x2-x. Они встречаются на iso-квадратах, содержащих углы окна выбора вы начали с ...
Если мы для удобства предположим, что x2 и y2 больше, чем x1 и y1 соответственно, нам нужно только перебирать iso-сетку для значений от x1 до x2 и y1 до y2, принимая только iso-квадраты, координаты y которых меньше обеих "больших" линий и меньше двух "меньших" линий.
