Экспорт нейронной сети, обученной с помощью MATLAB на других языках программирования
я обучил нейронную сеть с помощью набора инструментов нейронной сети MATLAB, и в частности с помощью команды nprtool, который предоставляет простой графический интерфейс для использования функций toolbox и экспорта net объект, содержащий информацию о сгенерированном NN.
таким образом, я создал рабочую нейронную сеть, которую я могу использовать в качестве классификатора, и диаграмма, представляющая ее, следующая:
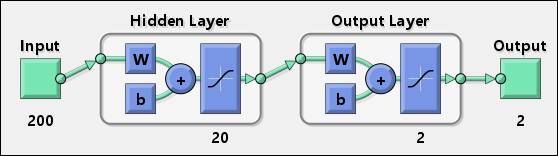
200 входных сигналов, 20 нейронов в первый скрытый слой и 2 нейрона в последнем слое, которые обеспечивают двумерный выход.
то, что я хочу сделать, это использовать сеть на каком-то другом языке программирования (C#, Java, ...).
чтобы решить эту проблему, я пытаюсь использовать следующий код в MATLAB:
y1 = tansig(net.IW{1} * input + net.b{1});
Results = tansig(net.LW{2} * y1 + net.b{2});
предполагая, что input представляет собой одномерный массив из 200 элементов, предыдущий код будет работать, если net.IW{1} является матрицей 20x200 (20 нейронов, 200 Весов).
в проблема в том, что я заметил, что size(net.IW{1}) возвращает неожиданное значение:
>> size(net.IW{1})
ans =
20 199
у меня такая же проблема с сетью с 10000 вход. В этом случае результат был не 20x10000, а что-то вроде 20x9384 (я не помню точное значение).
Итак, вопрос: как я могу получить веса каждого нейрона? И после этого кто-нибудь может объяснить мне, как я могу использовать их для получения того же результата MATLAB?
5 ответов
я решил проблемы, описанные выше, и я думаю, что полезно поделиться тем, что я узнал.
помещения
прежде всего, нам потребуется несколько определений. Рассмотрим следующее изображение, взятое из [1]:
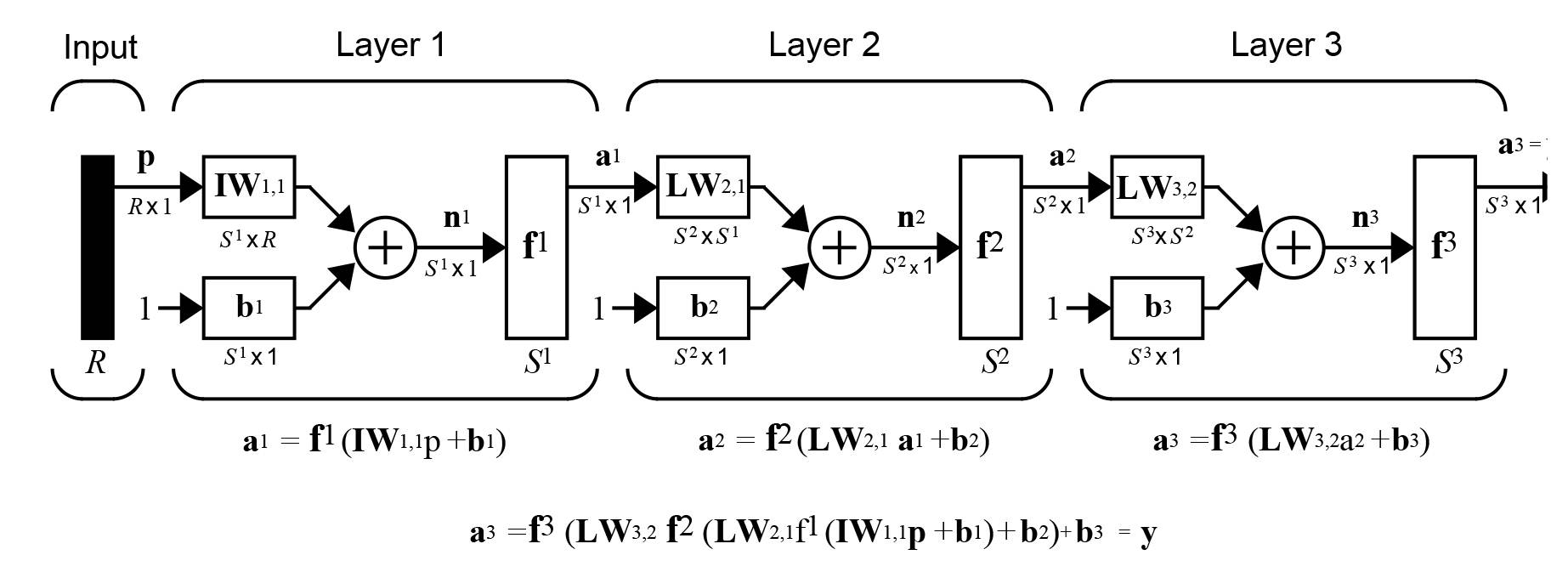
на приведенном выше рисунке,IW расшифровывается как начальные веса: они представляют собой веса нейронов на слое 1, каждый из которых соединен с каждым входом, как показано на следующем рисунке [1]:
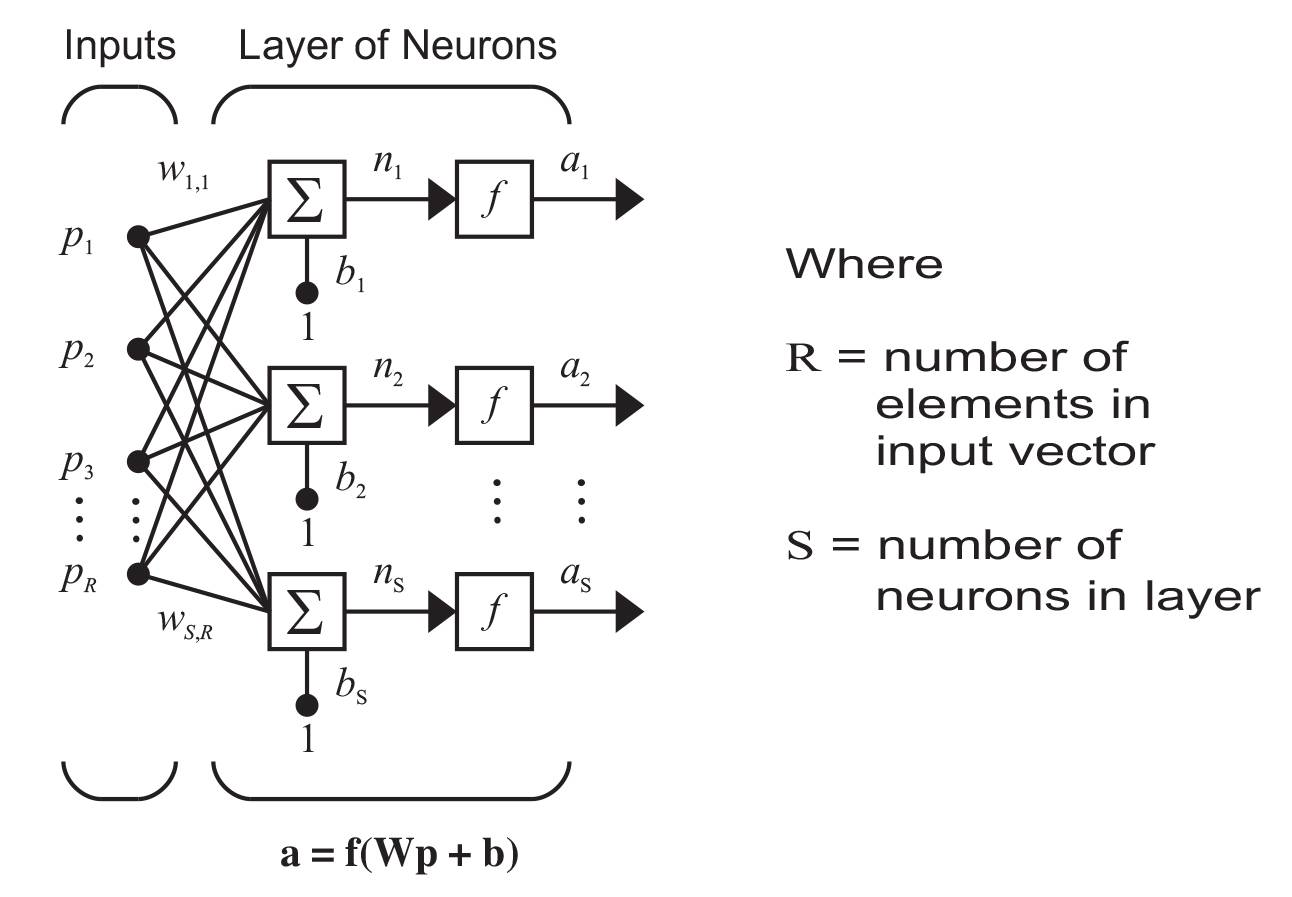
все остальные веса называются Весов слоя (LW на первом рисунке), которые также связаны с каждым выходом предыдущего слоя. В нашем случае мы используем сеть только с двумя слоями, поэтому мы будем использовать только один массив LW для решения наших проблем.
решение проблемы
После выше введение, мы можем продолжить, разделив вопрос в два этапа:
- заставить количество начальных Весов соответствовать длине входного массива
- используйте веса для реализации и использования нейронной сети, только что обученной на других языках программирования
A-принудительное число начальных весов, чтобы соответствовать длине входного массива
С помощью nprtool, мы можем обучать нашу сеть, и в конце процесс, мы также можем экспортировать в рабочей области некоторую информацию обо всем учебном процессе. В частности, нам необходимо экспортировать:
- сетевой объект MATLAB, представляющий созданную нейронную сеть
- входной массив, используемый для обучения сети
- целевой массив, используемый для обучения сети
кроме того, нам нужно создать M-файл, содержащий код, используемый MATLAB для создания нейронной сети, потому что нам нужно измените его и измените некоторые варианты обучения.
на следующем рисунке показано, как выполнять эти операции:
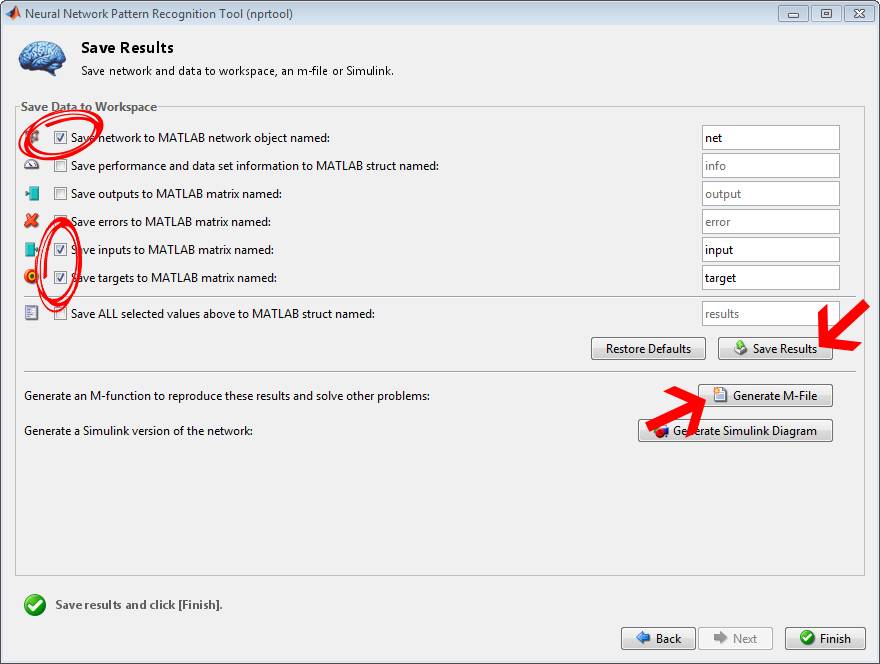
сгенерированный M-код будет похож на следующий:
function net = create_pr_net(inputs,targets)
%CREATE_PR_NET Creates and trains a pattern recognition neural network.
%
% NET = CREATE_PR_NET(INPUTS,TARGETS) takes these arguments:
% INPUTS - RxQ matrix of Q R-element input samples
% TARGETS - SxQ matrix of Q S-element associated target samples, where
% each column contains a single 1, with all other elements set to 0.
% and returns these results:
% NET - The trained neural network
%
% For example, to solve the Iris dataset problem with this function:
%
% load iris_dataset
% net = create_pr_net(irisInputs,irisTargets);
% irisOutputs = sim(net,irisInputs);
%
% To reproduce the results you obtained in NPRTOOL:
%
% net = create_pr_net(trainingSetInput,trainingSetOutput);
% Create Network
numHiddenNeurons = 20; % Adjust as desired
net = newpr(inputs,targets,numHiddenNeurons);
net.divideParam.trainRatio = 75/100; % Adjust as desired
net.divideParam.valRatio = 15/100; % Adjust as desired
net.divideParam.testRatio = 10/100; % Adjust as desired
% Train and Apply Network
[net,tr] = train(net,inputs,targets);
outputs = sim(net,inputs);
% Plot
plotperf(tr)
plotconfusion(targets,outputs)
прежде чем начать тренировочный процесс, нам нужно удалить все функции предварительной и последующей обработки что MATLAB выполняет на входах и выходах. Это можно сделать добавив следующие строки перед % Train and Apply Network строки:
net.inputs{1}.processFcns = {};
net.outputs{2}.processFcns = {};
после этих изменений create_pr_net() функция, просто мы можем использовать ее для создания нашей окончательной нейронной сети:
net = create_pr_net(input, target);
здесь input и target значения, которые мы экспортировали через nprtool.
таким образом, мы уверены, что количество весов равна длине входного массива. Кроме того, этот процесс полезен для упрощения переноса на другие языки программирования.
B-реализовать и использовать нейронные сети обучаются на других языках программирования
С этими изменениями, мы можем определить функцию, как это:
function [ Results ] = classify( net, input )
y1 = tansig(net.IW{1} * input + net.b{1});
Results = tansig(net.LW{2} * y1 + net.b{2});
end
в этом коде мы используем массивы IW и LW, упомянутые выше, но также предубеждения b, используемый в схеме сети nprtool. В этом контексте, мы не заботимся о роль предубеждения; просто, нам нужно использовать их потому что nprtool это делает.
теперь мы можем использовать classify() функция, определенная выше, или sim() функция одинаково, получая те же результаты, как показано в следующем примере:
>> sim(net, input(:, 1))
ans =
0.9759
-0.1867
-0.1891
>> classify(net, input(:, 1))
ans =
0.9759
-0.1867
-0.1891
очевидно, что classify() функция может быть интерпретирована как псевдокод, а затем реализована на всех языках программирования, в которых возможно определить MATLAB tansig() функция [2] и основные операции между массивами.
ссылки
[1] Говард Демут, Марк Бил, Мартин Хаган:Neural Network Toolbox 6-Руководство Пользователя, MATLAB
дополнительная информация
взгляните на robott ответ и ответ Сангун Чи для получения более подробной информации.
благодаря VitoShadow и robott answers я могу экспортировать значения нейронной сети Matlab в другие приложения.
Я очень ценю их, но я нашел некоторые тривиальные ошибки в их кодах и хочу их исправить.
1) в кодах VitoShadow,
Results = tansig(net.LW{2} * y1 + net.b{2});
-> Results = net.LW{2} * y1 + net.b{2};
2) в кодах предварительной обработки robott, Было бы проще извлечь xmax и xmin из переменной net, чем вычислить их.
xmax = net.inputs{1}.processSettings{1}.xmax
xmin = net.inputs{1}.processSettings{1}.xmin
3) в постобработке robott коды
xmax = net.outputs{2}.processSettings{1}.xmax
xmin = net.outputs{2}.processSettings{1}.xmin
Results = (ymax-ymin)*(Results-xmin)/(xmax-xmin) + ymin;
-> Results = (Results-ymin)*(xmax-xmin)/(ymax-ymin) + xmin;
вы можете вручную проверить и подтвердить значения следующим образом:
p2 = mapminmax('apply', net(:, 1), net.inputs{1}.processSettings{1})
-> обработанные данные
y1 = purelin ( net.LW{2} * tansig(net.iw{1}* p2 + net.b{1}) + net.b{2})
-> обработанные данные нейронной сети
y2 = mapminmax( 'reverse' , y1, net.outputs{2}.processSettings{1})
-> постобработки данных
ссылка: http://www.mathworks.com/matlabcentral/answers/14517-processing-of-i-p-data
Это небольшое улучшение к ответу великого Вито нееврея.
Если вы хотите используйте предварительную обработку и постобработку 'mapminmax' функции, вы должны обратить внимание, потому что "mapminmax" в Matlab нормализуется по строке, а не по столбцу!
это то, что вам нужно добавить в верхнюю функцию "классифицировать", чтобы сохранить когерентную предварительную/постобработку:
[m n] = size(input);
ymax = 1;
ymin = -1;
for i=1:m
xmax = max(input(i,:));
xmin = min(input(i,:));
for j=1:n
input(i,j) = (ymax-ymin)*(input(i,j)-xmin)/(xmax-xmin) + ymin;
end
end
и это в конце функция:
ymax = 1;
ymin = 0;
xmax = 1;
xmin = -1;
Results = (ymax-ymin)*(Results-xmin)/(xmax-xmin) + ymin;
это код Matlab, но его можно легко прочитать как псевдокод. Надеюсь, это будет полезно!
Я попытался реализовать просто 2-слойный NN в C++ с помощью OpenCV, а затем экспортировал веса в Android,который работал спокойно. Я написал небольшой скрипт, который генерирует файл заголовка с изученными весами,и это используется в следующем коде.
// Map Minimum and Maximum Input Processing Function
Mat mapminmax_apply(Mat x, Mat settings_gain, Mat settings_xoffset, double settings_ymin){
Mat y;
subtract(x, settings_xoffset, y);
multiply(y, settings_gain, y);
add(y, settings_ymin, y);
return y;
/* MATLAB CODE
y = x - settings_xoffset;
y = y .* settings_gain;
y = y + settings_ymin;
*/
}
// Sigmoid Symmetric Transfer Function
Mat transig_apply(Mat n){
Mat tempexp;
exp(-2*n, tempexp);
Mat transig_apply_result = 2 /(1 + tempexp) - 1;
return transig_apply_result;
}
// Map Minimum and Maximum Output Reverse-Processing Function
Mat mapminmax_reverse(Mat y, Mat settings_gain, Mat settings_xoffset, double settings_ymin){
Mat x;
subtract(y, settings_ymin, x);
divide(x, settings_gain, x);
add(x, settings_xoffset, x);
return x;
/* MATLAB CODE
function x = mapminmax_reverse(y,settings_gain,settings_xoffset,settings_ymin)
x = y - settings_ymin;
x = x ./ settings_gain;
x = x + settings_xoffset;
end
*/
}
Mat getNNParameter (Mat x1)
{
// convert double array to MAT
// input 1
Mat x1_step1_xoffsetM = Mat(1, 48, CV_64FC1, x1_step1_xoffset).t();
Mat x1_step1_gainM = Mat(1, 48, CV_64FC1, x1_step1_gain).t();
double x1_step1_ymin = -1;
// Layer 1
Mat b1M = Mat(1, 25, CV_64FC1, b1).t();
Mat IW1_1M = Mat(48, 25, CV_64FC1, IW1_1).t();
// Layer 2
Mat b2M = Mat(1, 48, CV_64FC1, b2).t();
Mat LW2_1M = Mat(25, 48, CV_64FC1, LW2_1).t();
// input 1
Mat y1_step1_gainM = Mat(1, 48, CV_64FC1, y1_step1_gain).t();
Mat y1_step1_xoffsetM = Mat(1, 48, CV_64FC1, y1_step1_xoffset).t();
double y1_step1_ymin = -1;
// ===== SIMULATION ========
// Input 1
Mat xp1 = mapminmax_apply(x1, x1_step1_gainM, x1_step1_xoffsetM, x1_step1_ymin);
Mat temp = b1M + IW1_1M*xp1;
// Layer 1
Mat a1M = transig_apply(temp);
// Layer 2
Mat a2M = b2M + LW2_1M*a1M;
// Output 1
Mat y1M = mapminmax_reverse(a2M, y1_step1_gainM, y1_step1_xoffsetM, y1_step1_ymin);
return y1M;
}
пример для смещения в заголовке может быть следующим:
static double b2[1][48] = {
{-0.19879, 0.78254, -0.87674, -0.5827, -0.017464, 0.13143, -0.74361, 0.4645, 0.25262, 0.54249, -0.22292, -0.35605, -0.42747, 0.044744, -0.14827, -0.27354, 0.77793, -0.4511, 0.059346, 0.29589, -0.65137, -0.51788, 0.38366, -0.030243, -0.57632, 0.76785, -0.36374, 0.19446, 0.10383, -0.57989, -0.82931, 0.15301, -0.89212, -0.17296, -0.16356, 0.18946, -1.0032, 0.48846, -0.78148, 0.66608, 0.14946, 0.1972, -0.93501, 0.42523, -0.37773, -0.068266, -0.27003, 0.1196}};
теперь, когда Google опубликовал Tensorflow, это стало устаревшим.
следовательно, решение становится (после исправления всех частей)
здесь я даю решение в Matlab, но если у вас есть функция tanh (), вы можете легко преобразовать его на любой язык программирования. Это просто для отображения полей из сетевого объекта и операций, которые вам нужны.
- Предположим, у вас есть обученный ann (сетевой объект), который вы хотите экспортировать
- предположим, что имя обученной Энн trained_ann
здесь скрипт для экспорта и тестирования. Тестовый скрипт сравнивает исходный сетевой результат с результатом my_ann_evaluation ()
% Export IT
exported_ann_structure = my_ann_exporter(trained_ann);
% Run and Compare
% Works only for single INPUT vector
% Please extend it to MATRIX version by yourself
input = [12 3 5 100];
res1 = trained_ann(input')';
res2 = my_ann_evaluation(exported_ann_structure, input')';
где вам нужны следующие две функции
первый my_ann_exporter:
function [ my_ann_structure ] = my_ann_exporter(trained_netw)
% Just for extracting as Structure object
my_ann_structure.input_ymax = trained_netw.inputs{1}.processSettings{1}.ymax;
my_ann_structure.input_ymin = trained_netw.inputs{1}.processSettings{1}.ymin;
my_ann_structure.input_xmax = trained_netw.inputs{1}.processSettings{1}.xmax;
my_ann_structure.input_xmin = trained_netw.inputs{1}.processSettings{1}.xmin;
my_ann_structure.IW = trained_netw.IW{1};
my_ann_structure.b1 = trained_netw.b{1};
my_ann_structure.LW = trained_netw.LW{2};
my_ann_structure.b2 = trained_netw.b{2};
my_ann_structure.output_ymax = trained_netw.outputs{2}.processSettings{1}.ymax;
my_ann_structure.output_ymin = trained_netw.outputs{2}.processSettings{1}.ymin;
my_ann_structure.output_xmax = trained_netw.outputs{2}.processSettings{1}.xmax;
my_ann_structure.output_xmin = trained_netw.outputs{2}.processSettings{1}.xmin;
end
второй my_ann_evaluation:
function [ res ] = my_ann_evaluation(my_ann_structure, input)
% Works with only single INPUT vector
% Matrix version can be implemented
ymax = my_ann_structure.input_ymax;
ymin = my_ann_structure.input_ymin;
xmax = my_ann_structure.input_xmax;
xmin = my_ann_structure.input_xmin;
input_preprocessed = (ymax-ymin) * (input-xmin) ./ (xmax-xmin) + ymin;
% Pass it through the ANN matrix multiplication
y1 = tanh(my_ann_structure.IW * input_preprocessed + my_ann_structure.b1);
y2 = my_ann_structure.LW * y1 + my_ann_structure.b2;
ymax = my_ann_structure.output_ymax;
ymin = my_ann_structure.output_ymin;
xmax = my_ann_structure.output_xmax;
xmin = my_ann_structure.output_xmin;
res = (y2-ymin) .* (xmax-xmin) /(ymax-ymin) + xmin;
end
