Эквивалентности двух автоматов
какой лучший или самый простой метод определения эквивалентности между двумя автоматами?
т. е., если заданы два конечных автомата A и B, как я могу определить, распознают ли они один и тот же язык?
Они оба детерминированы или оба недетерминированы.
3 ответов
два недетерминированных конечных automota (НОП) являются эквивалентными, если они принимают один и тот же язык.
чтобы определить, принимают ли они один и тот же язык, мы рассмотрим тот факт, что каждый NFA имеет минимальный DFA, где нет двух одинаковых состояний. Минимальный DFA также уникален. Таким образом, учитывая два NFA, если вы обнаружите, что их соответствующие минимальные DFA эквивалентны, то два NFA также должны быть эквивалентны.
для углубленного изучения этой темы я настоятельно рекомендую что Вы читаете введение в формальный язык и автоматы.
другой, более простой подход заключается в дополнении и пересечении автоматов. Автоматон A эквивалентно B iff L(A) содержится в L(B) и наоборот, который является iff пересечение между дополнением L(B) и L(A) пусто и наоборот.
вот алгоритм проверки, если L(A) содержится в L(B):
- дополнения: Во-первых, determinize
Bиспользование конструкции подмножества. Затем, пусть каждое принимающее государство отвергает, а каждое отвергающее государство принимает. Вы получаете автомат, который распознает дополнениеL(B). - пересечение: построить автомат, который распознает язык, который является пересечением дополнения
L(B)иL(A). То есть, построить автомат для пересечения автомата из Шага 1 иA. Пересечение двух автоматовUиVвы строите автомат с состояниямиU x V. Этот автомат движется из состояния(u,v)to(u',v')письмоaесли есть переходыu --a--> u'наUиv --a--> v'наV. Принимающие государства-это государства(u,v)здесьuпринимает вUиvпринимает вV. - после построения автомата на Шаге 2, все что нужно, это проверить пустоты. То есть, есть ли слово, которое принимает автомат? Это самая простая часть-найти путь в автомате от исходное состояние в принимающее состояние с использованием алгоритма BFS.
если L(A) содержится в L(B) нужно запустить тот же самый алгоритм, чтобы проверить, если L(B) содержится в L(A).
Я просто перефразирую ответ @Guy.
чтобы сравнить языки, принятые обоими, мы должны выяснить, если L(A) is equal to L(B) или нет.
таким образом, вы должны выяснить, если L(A)-L(B) and L(B)-L(A) имеет значение null или нет. (Reason1)
Часть 1:
чтобы узнать это, мы строим NFA X из NFA A и NFA B,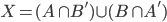
если X пустое множество, то L(A) = L(B) else L(A) != L(B). (Reason2)
Часть 2:
теперь мы должны найти эффективный способ доказать или опровергнуть X is empty set. Когда будет x пустым, как DFA или NFA? Ответ: X будет пустым, если нет пути, ведущего из начального состояния в любое конечное состояние X. Для этого можно использовать BFS или DFS.
Reason1: если оба имеют значение null, то L(A) = L(B).
Reason2: мы можем доказать, что множество регулярных языков замкнут относительно пересечения и союз. Таким образом, мы сможем создать NFA X эффективно.
и для наборов: