Факториал с использованием рекурсии в Java

сначала вы должны понять, как работает factorial.

давайте 4! в качестве примера.

4! = 4 * 3 * 2 * 1 = 24

давайте смоделируем код, используя пример выше:

int fact(int n)
    {
        int result;
       if(n==0 || n==1)
         return 1;

       result = fact(n-1) * n;
       return result;
    }

в большинстве языков программирования у нас есть то, что мы называем function stack. Это похоже на колоду карт, где каждая карта помещается над другой-и каждая карта может рассматриваться как функция, таким образом, передавая метод fact:

уровень стека 1: fact(4) // n = 4 and is not equal to 1. So we call fact(n-1)*n

стек Уровень 2: fact(3)

стек 3-го уровня: fact(2)

уровень стека 4:fact(1) / / теперь, n = 1. таким образом, мы возвращаем 1 из этой функции.

возврат значений...

стек 3-го уровня: 2 * fact(1) = 2 * 1 = 2

уровень стека 2:3 * fact(2) = 3 * 2 = 6

уровень стека 1: 4 * fact(3) = 4 * 6 = 24

Итак, у нас 24.

обратите внимание на эти строки:

result = fact(n-1) * n;
           return result;

или просто:

return fact(n-1) * n;

это вызывает функцию себя. Через 4 например,

в последовательности согласно стогам функции..

return fact(3) * 4;
return fact(2) * 3 * 4
return fact(1) * 2 * 3 * 4

подставляя результаты...

return 1 * 2 * 3 * 4 = return 24

надеюсь, вы поняли.

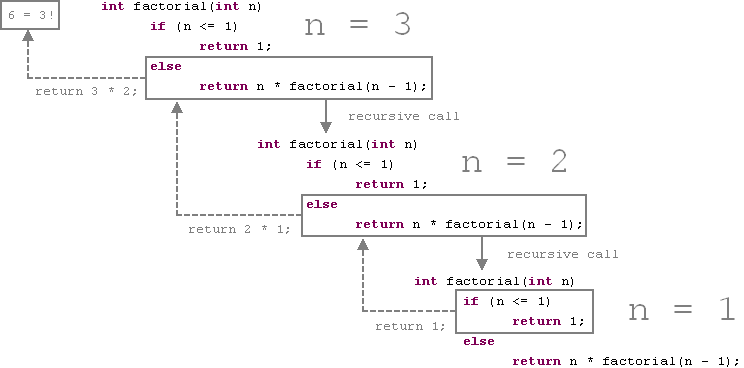
вот еще одно объяснение того, как вычисление факториала с помощью рекурсии строительство.

давайте немного изменим исходный код:

int factorial(int n) {
      if (n <= 1)
            return 1;
      else
            return n * factorial(n - 1);
}

вот расчет 3! подробнее:

источник: рекурсия (Java, C++) / алгоритмы и структуры данных

ваше замешательство, я полагаю, происходит от того, что вы думаете, что есть только один result переменной, тогда как на самом деле есть result переменной для каждого вызова функции. Поэтому старые результаты не заменяются,а возвращаются.

РАЗРАБОТКА:

int fact(int n)
{
    int result;

   if(n==1)
     return 1;

   result = fact(n-1) * n;
   return result;
}

предположим, что вызов fact(2):

int result;
if ( n == 1 ) // false, go to next statement
result = fact(1) * 2; // calls fact(1):
|    
|fact(1)
|    int result;  //different variable
|    if ( n == 1 )  // true
|        return 1;  // this will return 1, i.e. call to fact(1) is 1
result = 1 * 2; // because fact(1) = 1
return 2;

надеюсь, теперь понятнее.

что происходит, так это то, что сам рекурсивный вызов приводит к дальнейшему рекурсивному поведению. Если вы должны были написать его, вы получите:

 fact(4)
 fact(3) * 4;
 (fact(2) * 3) * 4;
 ((fact(1) * 2) * 3) * 4;
 ((1 * 2) * 3) * 4;

public class Factorial {

    public static void main(String[] args) {
        System.out.println(factorial(4));
    }

    private static long factorial(int i) {

        if(i<0)  throw new IllegalArgumentException("x must be >= 0"); 
        return i==0||i==1? 1:i*factorial(i-1);
    }
}

ключевым моментом, который вам не хватает здесь, является то, что переменная " результат "является переменной стека, и как таковая она не"заменяется". Чтобы уточнить, каждый раз, когда вызывается факт, новая переменная под названием "результат" создается внутри интерпретатора и связана с этим вызовом методов. Это в отличие от полей объекта, которые связаны с экземпляром объекта, а не с конкретным вызовом метода

хотя это старый, он по-прежнему довольно хорошо подходит в google. Поэтому я решил упомянуть об этом. Никто не упоминал, чтобы проверить, когда x = 0.

0! и 1! оба = 1.

Это не проверяется с предыдущими ответами и вызовет переполнение стека, если факт(0) был запущен. В любом случае простое исправление:

public static int fact(int x){
    if (x==1 | x==0)
        return 1;
    return fact(x-1) * x;
}// fact

рекурсивное решение с использованием тернарных операторов.

public static int fac(int n) {
    return (n < 1) ? 1 : n*fac(n-1);
}

на мой взгляд, и это мнение кого-то с начальным уровнем знаний java, я бы предложил, чтобы n == 1 было изменено на n

правильный:

int factorial(int n)
{
    if(n==0||n==1)
        return 1;
    else 
        return n*factorial(n-1);
}

это вернет 1 для факториала 0. Сделай это, поверь мне . Я понял это на собственном горьком опыте. Просто за то, что не сохранил условие для 0, не смог очистить интервью.

чтобы понять это, вы должны объявить метод самым простым способом, и Мартинас прибил его на 6 мая сообщение:

int fact(int n) {
    if(n==0) return 1;
    else return n * fact(n-1);
}

прочитайте вышеуказанную реализацию, и вы поймете.

IMHO, ключ для понимания действий, связанных с рекурсией:

1. во-первых, мы погружаемся в стек рекурсивно, и с каждым вызовом мы как изменить значение (например,n-1 на func(n-1);), который определяет, рекурсия должна идти все глубже и глубже.
2. раз recursionStopCondition выполняется (например,n == 0), рекурсии останавливаются, и методы выполняют фактическую работу и возвращают значения методу caller в верхние стога, таким образом клокоча к верхней части стек.
3. Это важно поймать значение, возвращаемое из более глубокого стека, каким-то образом измените его (умножение на n в вашем случае), а затем верните это измененное значение topwards стека. Распространенной ошибкой является то, что значение из самого глубокого кадра стека возвращается прямо наверх стека, так что все вызовы метода игнорируются.

конечно, методы могут выполнять полезную работу, прежде чем они погрузятся в рекурсию (сверху вниз стека) или по пути спина.

Не создавайте еще одну переменную

результат

просто

вернуть факт(n-1) * n;

class Calculation
{
    int fact(int n)
    {
        int result;

       if(n==1)
         return 1;

       return fact(n-1) * n;

    }
}

import java.util.Scanner;

public class Factorial {
    public static void main(String[] args) {
        Scanner keyboard = new Scanner(System.in);
        int n; 
        System.out.println("Enter number: ");
        n = keyboard.nextInt();
        int number = calculatefactorial(n);
        System.out.println("Factorial: " +number);
    }
    public static int calculatefactorial(int n){
        int factorialnumbers=1;
        while(n>0){
         factorialnumbers=(int)(factorialnumbers*n--);   
        }
        return factorialnumbers;
    }
}

public class Factorial2 {
    public static long factorial(long x) {
        if (x < 0) 
            throw new IllegalArgumentException("x must be >= 0");
        if (x <= 1) 
            return 1;  // Stop recursing here
        else 
           return x * factorial(x-1);  // Recurse by calling ourselves
    }
}

public class Factorial {
public static void main(String[] args) {
   int n = 7;
   int result = 1;
   for (int i = 1; i <= n; i++) {
       result = result * i;
   }
   System.out.println("The factorial of 7 is " + result);
}
}

Ну вот логика, чтобы найти факториал числа с помощью рекурсии,

static int factorialFunction(int n)
{
    int result;
    if(n == 1)
    {
       return 1;
    }
    // here we are calling the recursion function
    result = factorialFunction(n - 1) * n;
    return result;
}

между тем вы можете ссылаться этой ресурс для поиска примеров на факториале числа с использованием рекурсии.