Фильтр нижних частот Matlab c использованием fft

я реализовал простой фильтр нижних частот в matlab, используя прямой и обратный БПФ. Он работает в принципе, но минимальное и максимальное значения отличаются от оригинала.

signal = data;
%% fourier spectrum
% number of elements in fft
NFFT = 1024;
% fft of data
Y = fft(signal,NFFT)/L;
% plot(freq_spectrum)

%% apply filter
fullw = zeros(1, numel(Y));
fullw( 1 : 20 ) = 1;
filteredData = Y.*fullw;

%% invers fft
iY = ifft(filteredData,NFFT);
% amplitude is in abs part
fY = abs(iY);
% use only the length of the original data
fY = fY(1:numel(signal));
filteredSignal = fY * NFFT; % correct maximum

clf; hold on;
plot(signal, 'g-')
plot(filteredSignal ,'b-')
hold off;

полученное изображение выглядит следующим образом

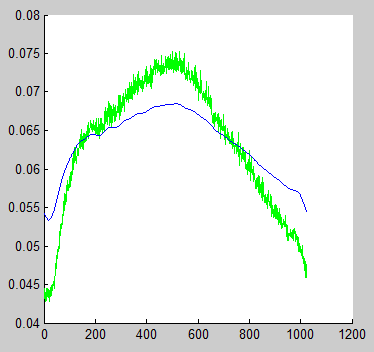
enter image description here

что я делаю не так? Если нормализовать обе данные, отфильтрованный сигнал будет выглядеть правильно.

7
fft filtering lowpass-filter matlab

1 ответов

просто чтобы напомнить себе о том, как MATLAB хранит частотный контент для Y = fft(y,N):

  • Y(1) - постоянное смещение
  • Y(2:N/2 + 1) - это набор положительных частот
  • Y(N/2 + 2:end) - это набор отрицательных частот... (обычно мы планируем это левый вертикальной оси)

для того, чтобы сделать истинный фильтр нижних частот, мы должны сохранить как низкие положительные частоты и низкий отрицательный частот.

вот пример того, как это делается с мультипликативным прямоугольным фильтром в частотной области, как вы это сделали:

% make our noisy function
t = linspace(1,10,1024);
x = -(t-5).^2  + 2;
y = awgn(x,0.5); 
Y = fft(y,1024);

r = 20; % range of frequencies we want to preserve

rectangle = zeros(size(Y));
rectangle(1:r+1) = 1;               % preserve low +ve frequencies
y_half = ifft(Y.*rectangle,1024);   % +ve low-pass filtered signal
rectangle(end-r+1:end) = 1;         % preserve low -ve frequencies
y_rect = ifft(Y.*rectangle,1024);   % full low-pass filtered signal

hold on;
plot(t,y,'g--'); plot(t,x,'k','LineWidth',2); plot(t,y_half,'b','LineWidth',2); plot(t,y_rect,'r','LineWidth',2);
legend('noisy signal','true signal','+ve low-pass','full low-pass','Location','southwest')

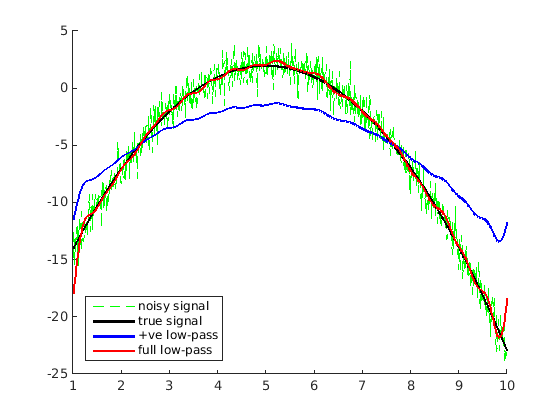
enter image description here

полный низкочастотный монтажник делает лучшую работу, но вы заметите, что реконструкция немного "волнистая". Это связано с тем, что умножение с функцией прямоугольника в частотной области совпадает с свертка с функцией sinc во временной области. Свертка с синкретизмом заменяет каждую точку очень неравномерным средневзвешенным значением ее соседей, отсюда и" волновой " эффект.

гауссовский фильтр имеет более приятные свойства фильтра нижних частот, потому что преобразование Фурье Гаусса является гауссовским. Гауссов распадается до нуля, поэтому он не включает дальних соседей в средневзвешенное значение во время свертки. Вот пример с гауссовым фильтром, сохраняющим положительное и отрицательное частоты:

gauss = zeros(size(Y));
sigma = 8;                           % just a guess for a range of ~20
gauss(1:r+1) = exp(-(1:r+1).^ 2 / (2 * sigma ^ 2));  % +ve frequencies
gauss(end-r+1:end) = fliplr(gauss(2:r+1));           % -ve frequencies
y_gauss = ifft(Y.*gauss,1024);

hold on;
plot(t,x,'k','LineWidth',2); plot(t,y_rect,'r','LineWidth',2); plot(t,y_gauss,'c','LineWidth',2);
legend('true signal','full low-pass','gaussian','Location','southwest')

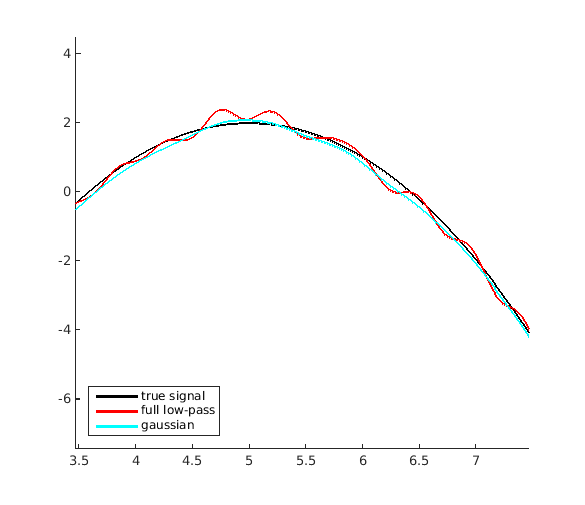
enter image description here

как вы можете видеть, реконструкции намного лучше.

16