Функция рекурсии в Python
рассмотрим эту базовую рекурсию в Python:
def fibonacci(number):
if number == 0: return 0
elif number == 1:
return 1
else:
return fibonacci(number-1) + fibonacci(number-2)
что имеет смысл в соответствии с (n-1) + (n-2) функцией ряда Фибоначчи.
как Python выполняет рекурсию, которая содержит другую рекурсию не внутри, а внутри той же строки кода? Завершает ли "finobacci(number-1)" всю рекурсию, пока не достигнет "1", а затем делает то же самое с "Фибоначчи(number-2)" и добавляет их?
для сравнения, следующий рекурсивный функция для поднятия числа " x "в мощность "y", я могу понять рекурсию, def power , вызывающую себя до y==0, так как в одной строке есть только один рекурсивный вызов. Все же не должны ли все результаты быть "1", так как последняя выполненная команда "возвращает 1", когда y==0, поэтому x не возвращается?
def power(x, y):
if y == 0:
return 1
else:
return x*power(x, y-1)
9 ответов
в выражении fibonacci(number-1) + fibonacci(number-2) первый вызов функции должен быть завершен до вызова второго вызова функции.
таким образом, весь стек рекурсии для первого вызова должен быть завершен до начала второго вызова.
Короткий Ответ:
каждый раз, когда Python "видит"fibonacci() Он делает другой вызов функции и не продвигается дальше, пока не закончит этот вызов функции.
пример
Итак, предположим, что это оценка fibonacci(4).
как только он доберется до строки return fibonacci(number-1) + fibonacci(number-2), он "видит" вызов fibonacci(number-1).
Итак, теперь он работает fibonacci(3) - он не видел fibonacci(number-2) вообще пока. Для запуска fibonacci(3), он должен выяснить fibonacci(2)+fibonacci(1). Опять же, он запускает первый функцию он видит, которая на этот раз fibonacci(2).
теперь он, наконец, попадает в базовый случай, когда fibonacci(2) запускается. Он оценивает fibonacci(1), который возвращает 1, тогда, в первый раз, он может продолжать + fibonacci(number-2) часть fibonacci() звонок. fibonacci(0) возвращает 0, который затем позволяет fibonacci(2) возвращение 1.
теперь fibonacci(3) получил значение, возвращенное из fibonacci(2), он может прогрессировать до оценки fibonacci(number-2) (fibonacci(1)).
этот процесс продолжается до тех пор, пока все не будет оценено и fibonacci(4) может возвратить 3.
чтобы увидеть, как проходит вся оценка, следуйте стрелкам на этой диаграмме:
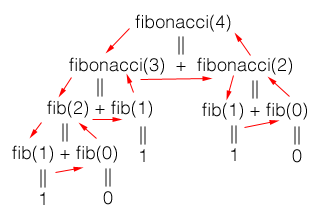
завершает ли "finobacci(число-1)" всю рекурсию, пока не достигнет "1", а затем делает то же самое с "Фибоначчи(число-2)" и добавляет их?
Да, именно так. Другими словами, следующее
return fibonacci(number-1) + fibonacci(number-2)
эквивалентно
f1 = fibonacci(number-1)
f2 = fibonacci(number-2)
return f1 + f2
Я бы очень рекомендовал вам поместить свой код в Python tutor.
вы сможете получить его на лету. См. stackframe, ссылки и т. д.
можно использовать rcviz модуль для визуализации рекурсий, просто добавив декоратор к рекурсивной функции.
вот визуализация для вашего кода выше:
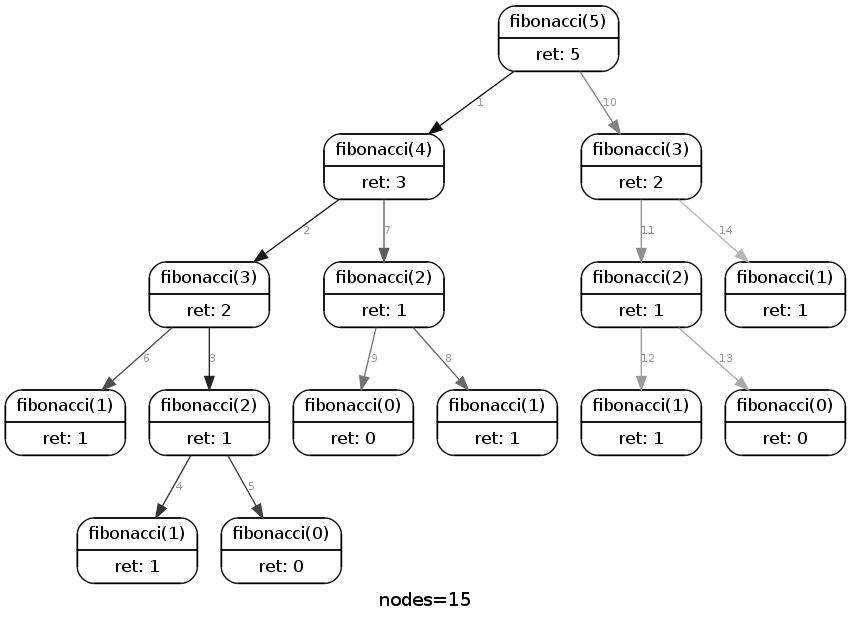
ребра нумеруются по порядку, в котором они были пройдены исполнения. Края выцветают от черного до серого, чтобы указать порядок обхода: сначала черные края, затем серые края.
(Я написал модуль rcviz на GitHub.)
вы можете понять это сами, поместив функцию печати в функцию и добавив глубину, чтобы мы могли распечатать ее красивее:
def fibonacci(number, depth = 0):
print " " * depth, number
if number == 0:
return 0
elif number == 1:
return 1
else:
return fibonacci(number-1, depth + 1) + fibonacci(number-2, depth + 1)
вызов fibonacci(5) дает нам:
5
4
3
2
1
0
1
2
1
0
3
2
1
0
1
мы видим, что 5 звонки 4, который идет к завершению, а затем он вызывает 3, который затем переходит к завершению.
Python делает вещи слева направо, когда это возможно. Исключения из этого правила заключены в квадратные скобки.
на x*power(x, y-1): x оценивается после power оценивается
а в fibonacci(number-1) + fibonacci(number-2), fibonacci(number-1) оценивается (рекурсивно, пока не остановится), а затем fibonacci(number-1) оценивается
ваши вторые функции рекурсии делают это (пример), поэтому 1 не будет возвращен.
power(2, 3)
2 * power(2, 2)
2 * 2 * power(1,2)
2 * 2 * 2 * power(0,2) # Reaching base case
2 * 2 * 2 * 1
8
