Gaussian подходит для Python
Я пытаюсь подогнать Гаусса для моих данных (который уже является грубым Гауссом). Я уже воспользовался советом тех, кто здесь, и попытался curve_fit и leastsq но я думаю, что мне не хватает чего-то более фундаментального (в том, что я понятия не имею, как использовать команду).
Вот посмотрите на сценарий, который у меня есть до сих пор
import pylab as plb
import matplotlib.pyplot as plt
# Read in data -- first 2 rows are header in this example.
data = plb.loadtxt('part 2.csv', skiprows=2, delimiter=',')
x = data[:,2]
y = data[:,3]
mean = sum(x*y)
sigma = sum(y*(x - mean)**2)
def gauss_function(x, a, x0, sigma):
return a*np.exp(-(x-x0)**2/(2*sigma**2))
popt, pcov = curve_fit(gauss_function, x, y, p0 = [1, mean, sigma])
plt.plot(x, gauss_function(x, *popt), label='fit')
# plot data
plt.plot(x, y,'b')
# Add some axis labels
plt.legend()
plt.title('Fig. 3 - Fit for Time Constant')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.show()
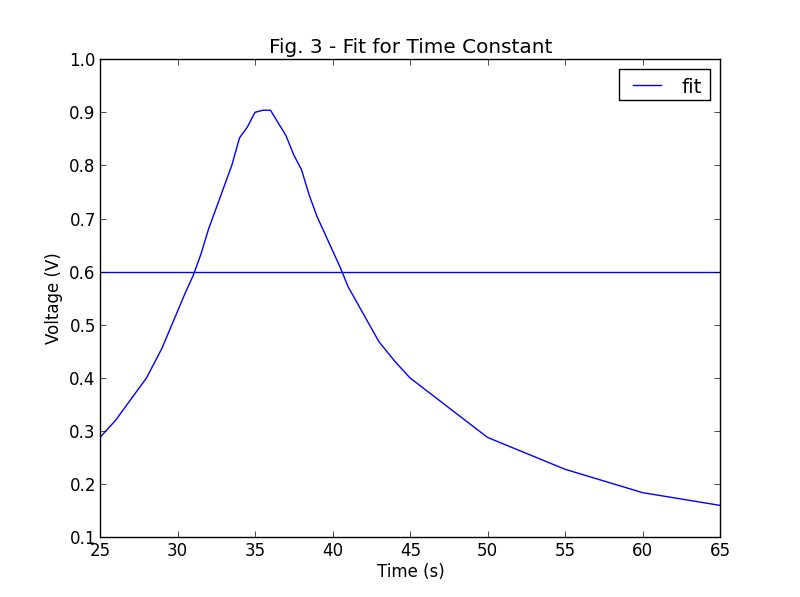
то, что я получаю от этого, - это Гауссовская форма, которая является моими исходными данными, и прямая горизонтальная линия.
кроме того, я хотел бы построить свой график с использованием точек, а не их подключения. Любой вклад приветствуется!
6 ответов
вот исправленный код:
import pylab as plb
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy import asarray as ar,exp
x = ar(range(10))
y = ar([0,1,2,3,4,5,4,3,2,1])
n = len(x) #the number of data
mean = sum(x*y)/n #note this correction
sigma = sum(y*(x-mean)**2)/n #note this correction
def gaus(x,a,x0,sigma):
return a*exp(-(x-x0)**2/(2*sigma**2))
popt,pcov = curve_fit(gaus,x,y,p0=[1,mean,sigma])
plt.plot(x,y,'b+:',label='data')
plt.plot(x,gaus(x,*popt),'ro:',label='fit')
plt.legend()
plt.title('Fig. 3 - Fit for Time Constant')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.show()
результат: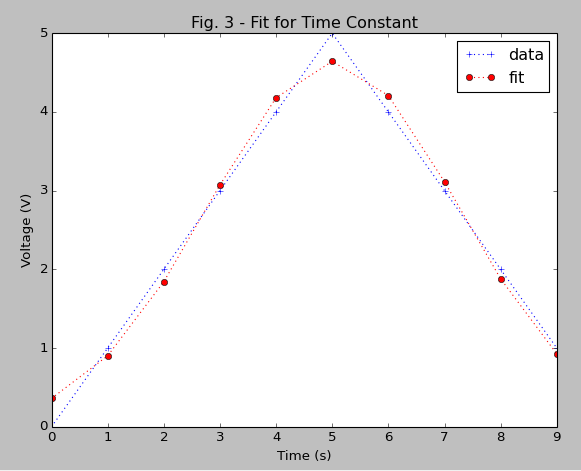
объяснение
вам нужны хорошие начальные значения, такие, что curve_fit функция сходится при" хороших " значениях. Я не могу сказать, почему ваша подгонка не сходилась (хотя определение вашего среднего странно-проверьте ниже), но я дам вам стратегию, которая работает для ненормализованных гауссовых функций, таких как ваша.
пример
оценочные параметры должны быть близки к конечным значениям (используйте взвешенный арифметический имею в виду - делим на сумму всех значений):
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import numpy as np
x = np.arange(10)
y = np.array([0, 1, 2, 3, 4, 5, 4, 3, 2, 1])
# weighted arithmetic mean (corrected - check the section below)
mean = sum(x * y) / sum(y)
sigma = np.sqrt(sum(y * (x - mean)**2) / sum(y))
def Gauss(x, a, x0, sigma):
return a * np.exp(-(x - x0)**2 / (2 * sigma**2))
popt,pcov = curve_fit(Gauss, x, y, p0=[max(y), mean, sigma])
plt.plot(x, y, 'b+:', label='data')
plt.plot(x, Gauss(x, *popt), 'r-', label='fit')
plt.legend()
plt.title('Fig. 3 - Fit for Time Constant')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.show()
я лично предпочитаю использовать numpy.
комментарий к определению среднего (включая ответ разработчика)
так как рецензентам не понравился мой редактировать на # Developer's code, я объясню, для какого случая я бы предложил улучшенный код. Среднее значение разработчика не соответствует одному из нормальных определений среднего.
ваше определение возвращает:
>>> sum(x * y)
125
>>> sum(x * y) / len(x)
12.5 #for Python 3.x
взвешенное среднее арифметическое:
>>> sum(x * y) / sum(y)
5.0
аналогично вы можете сравнить определения стандартного отклонения (sigma). Сравните с фигурой получившейся подгонки:
комментарий для Python 2.X пользователи
В Python 2.x вы должны дополнительно использовать новое подразделение, чтобы не столкнуться с странными результатами или преобразовать числа перед делением явно:
from __future__ import division
или например
sum(x * y) * 1. / sum(y)
вы получаете горизонтальную прямую линию, потому что она не сходилась.
Лучшая сходимость достигается, если первый параметр фитинга(p0) ставится как max (y), 5 в примере вместо 1.
после потери часов, пытаясь найти мою ошибку, проблема заключается в вашей формуле:
sigma = sum(y*(x-mean)**2)/n это неправильно, правильная формула-квадрат этого!;
sqrt (sum (y*(x-mean)**2) / n)
надеюсь, что это помогает
есть и другой способ выполнения приспособления, которые с помощью 'lmfit' пакет. Он в основном использует cuve_fit, но намного лучше подходит и предлагает сложную установку. Подробные пошаговые инструкции приведены ниже ссылке. http://cars9.uchicago.edu/software/python/lmfit/model.html#model.best_fit