Генерация целых чисел в порядке возрастания с использованием набора простых чисел
У меня есть набор простых чисел, и я должен генерировать целые числа, используя только эти простые факторы в порядке возрастания.
например, если набор p = {2, 5}, то мои чисел должно быть 1, 2, 4, 5, 8, 10, 16, 20, 25, ...
есть ли эффективный алгоритм для решения этой проблемы?
4 ответов
основная идея заключается в том, что 1 является членом множества, и для каждого члена множества n так же 2n и 5n являются членами набора. Таким образом, вы начинаете с вывода 1 и нажимаете 2 и 5 в очередь приоритетов. Затем вы повторно вставляете передний элемент очереди приоритетов, выводите его, если он отличается от предыдущего вывода, и нажимаете 2 раза и 5 раз число в очередь приоритетов.
Google для "номера Хэмминга" или "обычный номер" или перейдите в A003592 чтобы узнать больше.
----- ДОБАВЛЕНО ПОЗЖЕ -----
я решил потратить несколько минут в обеденный перерыв, чтобы написать программу для реализации описанного выше алгоритма, с помощью языка программирования Scheme. Во-первых, здесь - это реализация библиотек очередей приоритетов с использованием алгоритма сопряжения кучи:
(define pq-empty '())
(define pq-empty? null?)
(define (pq-first pq)
(if (null? pq)
(error 'pq-first "can't extract minimum from null queue")
(car pq)))
(define (pq-merge lt? p1 p2)
(cond ((null? p1) p2)
((null? p2) p1)
((lt? (car p2) (car p1))
(cons (car p2) (cons p1 (cdr p2))))
(else (cons (car p1) (cons p2 (cdr p1))))))
(define (pq-insert lt? x pq)
(pq-merge lt? (list x) pq))
(define (pq-merge-pairs lt? ps)
(cond ((null? ps) '())
((null? (cdr ps)) (car ps))
(else (pq-merge lt? (pq-merge lt? (car ps) (cadr ps))
(pq-merge-pairs lt? (cddr ps))))))
(define (pq-rest lt? pq)
(if (null? pq)
(error 'pq-rest "can't delete minimum from null queue")
(pq-merge-pairs lt? (cdr pq))))
теперь для алгоритма. Функция f принимает два параметра, список числа в наборе ps и n элементов для вывода из головки вывода. Алгоритм немного изменен; приоритетная очередь инициализируется нажатием 1, затем начинаются шаги извлечения. Переменная p - предыдущее выходное значение (изначально 0),pq приоритет очереди, и xs - это список вывода, который накапливается в обратном порядке. Вот код:
(define (f ps n)
(let loop ((n n) (p 0) (pq (pq-insert < 1 pq-empty)) (xs (list)))
(cond ((zero? n) (reverse xs))
((= (pq-first pq) p) (loop n p (pq-rest < pq) xs))
(else (loop (- n 1) (pq-first pq) (update < pq ps)
(cons (pq-first pq) xs))))))
для тех, не знаком со схемой, loop является локально определенной функцией, которая вызывается рекурсивно, и cond является главой цепочки if-else; в этом случае их три cond предложения, каждое предложение с предикатом и следствием, с последующим вычисляется для первого предложения, для которого предикат истинен. Предикат (zero? n) завершает рекурсию и возвращает список вывода в правильном порядке. Предикат (= (pq-first pq) p) указывает, что текущий руководитель очереди приоритетов вывод ранее, поэтому он пропускается путем повторения с остальной частью очереди приоритетов после первого элемента. Наконец,else предикат, который всегда истинен, определяет новое число для вывода, поэтому он уменьшает счетчик, сохраняет текущую головку очереди приоритетов как новое Предыдущее значение, обновляет очередь приоритетов для добавления новых дочерних элементов текущего числа и вставляет текущую головку очереди приоритетов в накапливающийся вывод.
так как это нетривиально обновить очередь приоритетов, чтобы добавить новые дочерние элементы текущего номера, эта операция извлекается в отдельную функцию:
(define (update lt? pq ps)
(let loop ((ps ps) (pq pq))
(if (null? ps) (pq-rest lt? pq)
(loop (cdr ps) (pq-insert lt? (* (pq-first pq) (car ps)) pq)))))
функция петляет по элементам ps set, вставляя каждый в очередь приоритетов;if возвращает обновленную очередь приоритетов, за вычетом ее старой головки, когда ps список не будет исчерпан. Рекурсивный шаг обнажает голову ps список cdr и вставляет продукт головки приоритетная очередь и руководитель ps список в очереди приоритетов.
вот два примера алгоритма:
> (f '(2 5) 20)
(1 2 4 5 8 10 16 20 25 32 40 50 64 80 100 125 128 160 200 250)
> (f '(2 3 5) 20)
(1 2 3 4 5 6 8 9 10 12 15 16 18 20 24 25 27 30 32 36)
вы можете запустить программу в http://ideone.com/sA1nn.
удаление номера и вставляю все его кратные (по простым числам в наборе) в очередь приоритетов -неправильно (в смысле, вопрос) - т. е. он производит правильную последовательность а неэффективно так.
это неэффективно двумя способами - Во-первых, это перепроизводит последовательность; во-вторых, каждая операция PriorityQueue несет дополнительные расходы (операции remove_top и insert обычно не так O (1), конечно,не в любой реализации PriorityQueue на основе списка или дерева).
эффективное O (n) алгоритм поддерживает указатели обратно в саму последовательность по мере ее создания, чтобы найти и добавить следующее число в O (1). В псевдокоде:
return array h where
h[0]=1; n=0; ps=[2,3,5, ... ]; // base primes
is=[0 for each p in ps]; // indices back into h
xs=[p for each p in ps] // next multiples: xs[k]==ps[k]*h[is[k]]
repeat:
h[++n] := minimum xs
for each (i,x,p) in (is,xs,ps):
if( x==h[n] )
{ x := p*h[++i]; } // advance the minimal multiple/pointer
для каждого минимального кратного он продвигает свой указатель, в то же время вычисляя его следующее кратное значение. Это слишком эффективно реализует PriorityQueue, но с решающими различиями-это до конечная точка, а не после; он не создает никакого дополнительного хранилища, кроме самой последовательности; и его размер постоянен (просто k для k базовые простые числа), тогда как размер past-the-end PriorityQueue растет по мере продвижения по последовательности (в случае последовательности Хэмминга, основанной на множестве 3 простые числа, as n2/3, для n чисел последовательности).
классический последовательность Хэмминга в Haskell по сути тот же алгоритм:
h = 1 : map (2*) h `union` map (3*) h `union` map (5*) h
union a@(x:xs) b@(y:ys) = case compare x y of LT -> x : union xs b
EQ -> x : union xs ys
GT -> y : union a ys
мы можем создать ровные цифры на произвольные базовые простые числа с помощью (2016-08-18: основное ускорение из-за использования Int вместо Integer где это возможно, даже на 32-бит; дополнительные 20% благодаря настройке, предложенной @GordonBGood, в результате чего сложность размера полосы до O (n1/3)).
это обсуждается еще в ответ где мы также находим его полную атрибуцию:
slice hi w = (c, sortBy (compare `on` fst) b) where -- hi is a top log2 value
lb5=logBase 2 5 ; lb3=logBase 2 3 -- w<1 (NB!) is (log2 width)
(Sum c, b) = fold -- total count, the band
[ ( Sum (i+1), -- total triples w/this j,k
[ (r,(i,j,k)) | frac < w ] ) -- store it, if inside the band
| k <- [ 0 .. floor ( hi /lb5) ], let p = fromIntegral k*lb5,
j <- [ 0 .. floor ((hi-p)/lb3) ], let q = fromIntegral j*lb3 + p,
let (i,frac) = pr (hi-q) ; r = hi - frac -- r = i + q
] -- (sum . map fst &&& concat . map snd)
pr = properFraction
это можно обобщить для k база простых чисел, а также, вероятно, работает в O (n(k-1)/k) времени.
посмотреть это так запись для важного последующего развития. кроме того, ответ это интересно. и еще ... --104-->обзоры ответа.
этот 2-мерный алгоритм исследования не является точным, но работает для первых 25 целых чисел, а затем смешивает 625 и 512.
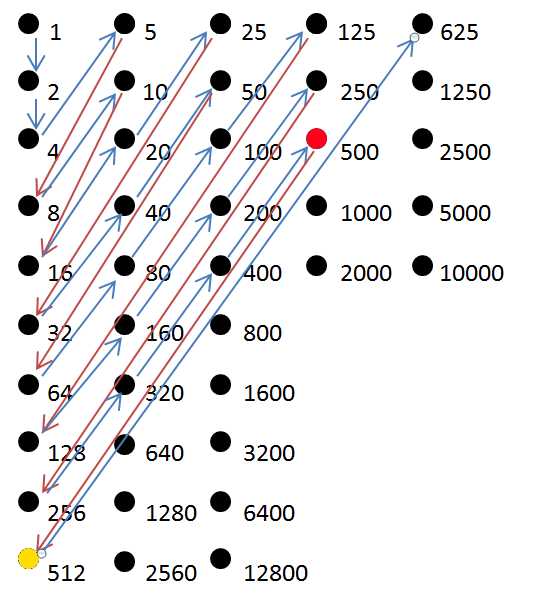
n = 0
exp_before_5 = 2
while true
i = 0
do
output 2^(n-exp_before_5*i) * 5^Max(0, n-exp_before_5*(i+1))
i <- i + 1
loop while n-exp_before_5*(i+1) >= 0
n <- n + 1
end while
основываясь на ответе user448810, вот решение, которое использует кучи и векторы из STL.
Теперь кучи обычно выводят наибольшее значение, поэтому мы храним отрицательные числа в качестве обходного пути (так как a>b <==> -a<-b).
#include <vector>
#include <iostream>
#include <algorithm>
int main()
{
std::vector<int> primes;
primes.push_back(2);
primes.push_back(5);//Our prime numbers that we get to use
std::vector<int> heap;//the heap that is going to store our possible values
heap.push_back(-1);
std::vector<int> outputs;
outputs.push_back(1);
while(outputs.size() < 10)
{
std::pop_heap(heap.begin(), heap.end());
int nValue = -*heap.rbegin();//Get current smallest number
heap.pop_back();
if(nValue != *outputs.rbegin())//Is it a repeat?
{
outputs.push_back(nValue);
}
for(unsigned int i = 0; i < primes.size(); i++)
{
heap.push_back(-nValue * primes[i]);//add new values
std::push_heap(heap.begin(), heap.end());
}
}
//output our answer
for(unsigned int i = 0; i < outputs.size(); i++)
{
std::cout << outputs[i] << " ";
}
std::cout << std::endl;
}
выход:
1 2 4 5 8 10 16 20 25 32
